White solving logarithmic equations or logarithmic
inequalities care must be taken to ensure that the value
of the variable obtained do indeed satisfy the given
equation . Often the solution consists in transforming the original equation to form which can be solved with ease .
But in bargain the process the transformations carried
out are hot always equivalent .In what follows one must
verify that the values of veriables obtained indeed satisfy
original equation or inequation.
Let S be the set of all solutions x in real numbers of
the equation (log5x)2+log5x(5)x=1 . Then ∑x∈Sx
A
126
B
15125
C
13125
D
131
Text Solution
The correct Answer is:2
|
Topper's Solved these Questions
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTECHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - E) Assertion-Reason
13 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTECHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - G) Integer
6 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTECHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - C) More than one option are correct
11 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions
8 Videos
- SETS BOOK - AAKASH INSTITUTECHAPTER - SETS EXERCISE - SECTION-I(Aakash Challengers Questions)
5 Videos
Similar Questions
While solving logarithmic equations or logarithmic
inequalities care must be taken to ensure that the value
of the variable obtained do indeed satisfy the given
equation . Often the solution consists in transforming the original equation to form which can be solved with ease .
But in bargain the process the transformations carried
out are not always equivalent .In what follows one must
verify that the values of variables obtained indeed satisfy
original equation or inequation.
How many solutions in real numbers does the
equation 3x8xx−2=6 have ?
i) None
ii) Exactly one
iii) Exactly two
iv) Infinite
View SolutionStandard Logarithmic Inequalities
View Solution
Knowledge Check
White solving logarithmic equations or logarithmic
inequalities care must be taken to ensure that the value
of the variable obtained do indeed satisfy the given
equation . Often the solution consists in transforming the original equation to form which can be solved with ease .
But in bargain the process the transformations carried
out are hot always equivalent .In what follows one must
verify that the values of veriables obtained indeed satisfy
original equation or inequation.
How many solutions in real numbers does the
equation 3x8xx−2=6 have ?ANoneBExactly oneCExactly twoDInfiniteWhite solving logarithmic equations or logarithmic
inequalities care must be taken to ensure that the value
of the variable obtained do indeed satisfy the given
equation . Often the solution consists in transforming the original equation to form which can be solved with ease .
But in bargain the process the transformations carried
out are hot always equivalent .In what follows one must
verify that the values of veriables obtained indeed satisfy
original equation or inequation.
The solution of the inequality
The solution of the inequality
xlog110(x2+x=1)>0
is given byA−∞<x<2B−∞<x<−1C−3<x<1D1<x<3 Above transformation can be carried out by :AH+/Δ,Zn(Hg),HClBHIO4,LiAlH4CHIO4,H+/ΔDH+/Δ,HIO4
Above transformation can be carried out by :AH+/Δ,Zn(Hg),HClBHIO4,LiAlH4CHIO4,H+/ΔDH+/Δ,HIO4

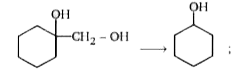 Above transformation can be carried out by :
Above transformation can be carried out by :