A point P is taken at random on a straight line AB. The chance that the greater of the parts AP and PB is at least k times the smaller is
2k+1
2k+2
2K2+1
2K2+2
The correct Answer is:D
Topper's Solved these Questions
- PROBABILITYBOOK - AAKASH INSTITUTECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT SECTION-I (subjective type questions)
10 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
12 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions
8 Videos
Similar Questions
Knowledge Check
Two point P, Q are taken at random on a straight line OA of length a. The chance that PQ>b, where b<a is
A|a−b|aB|b−a|aC(a−b)2a2D(b−a)2b2If two points are taken at random on the circumference of circle, the chance that their distance apart is greater than the radius of the circle is
A14B13C23D34
If P is the mid point of line segment AB , then what is the relation between AP an PB ?
View SolutionSuppose a point C is on straight line AB and two circles of diameter AC and AB are drawn. A point P is on the circumference of the circle with diameter AB. If AP meet to other circle at Q then which is correct-
View SolutionThe decimal part of logarithm of two numbers taken at random are found to seven places. The chance that second can be subtracted from the first
View SolutionSplit 207 into three parts such that these parts are in A.P. and the product of the two smaller parts is 4623.
View SolutionStatement 1: Our of 5 tickets consecutively numbered, three are drawn at random. The chance that the numbers on them are in A.P. is 2/15.
Statement 2: Out of 2n+1 tickets consecutively numbered, three are drawn at random, the chance that the numbers on them are in A.P. is 3n/(4n2−1).
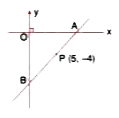
View SolutionThe point P (5,-4) divides the line segment AB, as shown in the figure, P (5, 4) in the ratio 2:5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
View Solution
