Find the tension in the strings AC and BC shown in figure.
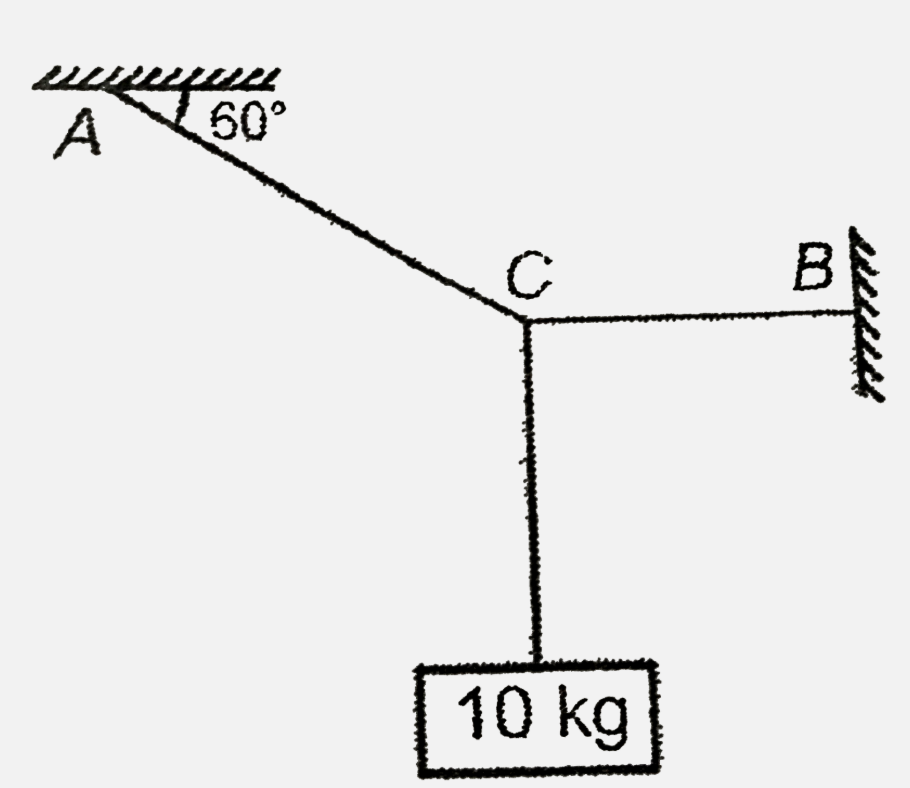
FBD of point C:
C is at equilibrium , so
T2sin60∘=100N
⇒T2=100sin60∘N
200√3N
Again , T1=T2cos60∘
=200√3×12
=100√3N

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -A)
48 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
33 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Illustration
5 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Knowledge Check
The tension in the string shown in figure m−2m→F is.
AF/3BF/6CF/2D2FCalculate the tension in the string shown in the figure. All the surfaces are frictionless. (Take g=10/ms−1)
 A2.5 NB5 NC7.5 ND10 N
A2.5 NB5 NC7.5 ND10 NFind the tension T2 in the system shown in the figure.
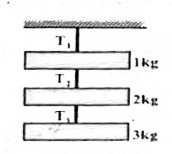 A1gNB2gNC5gND6gN
A1gNB2gNC5gND6gN
Determine the tensions T1 and T2 in the strings as shown in figure.
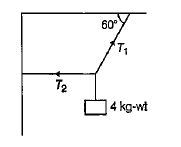
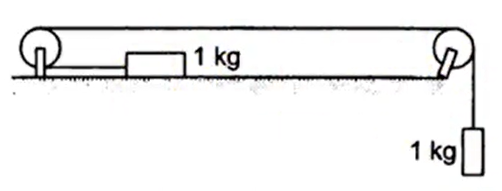
View SolutionCalculate the tension in the string shown in figure. The pulley and the string are light and all surfaces are frictionless. Take g=10 m/s2.
View Solution(a) A box of weight 10√3 N is held n equilibrium with the help of two strings OA and OB as shown in figure-1. the string OA is horizontal. Find the tensions in both the stings.

(b) If you can change location of the point A on the wall and hence the orientation of the string OA without altering the orientation of the string OB as shown in figure-II. what angle should the string OA make with the wall so that a minimum tension is developed in it?
View SolutionThe tension T in the string shown in figure is

View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
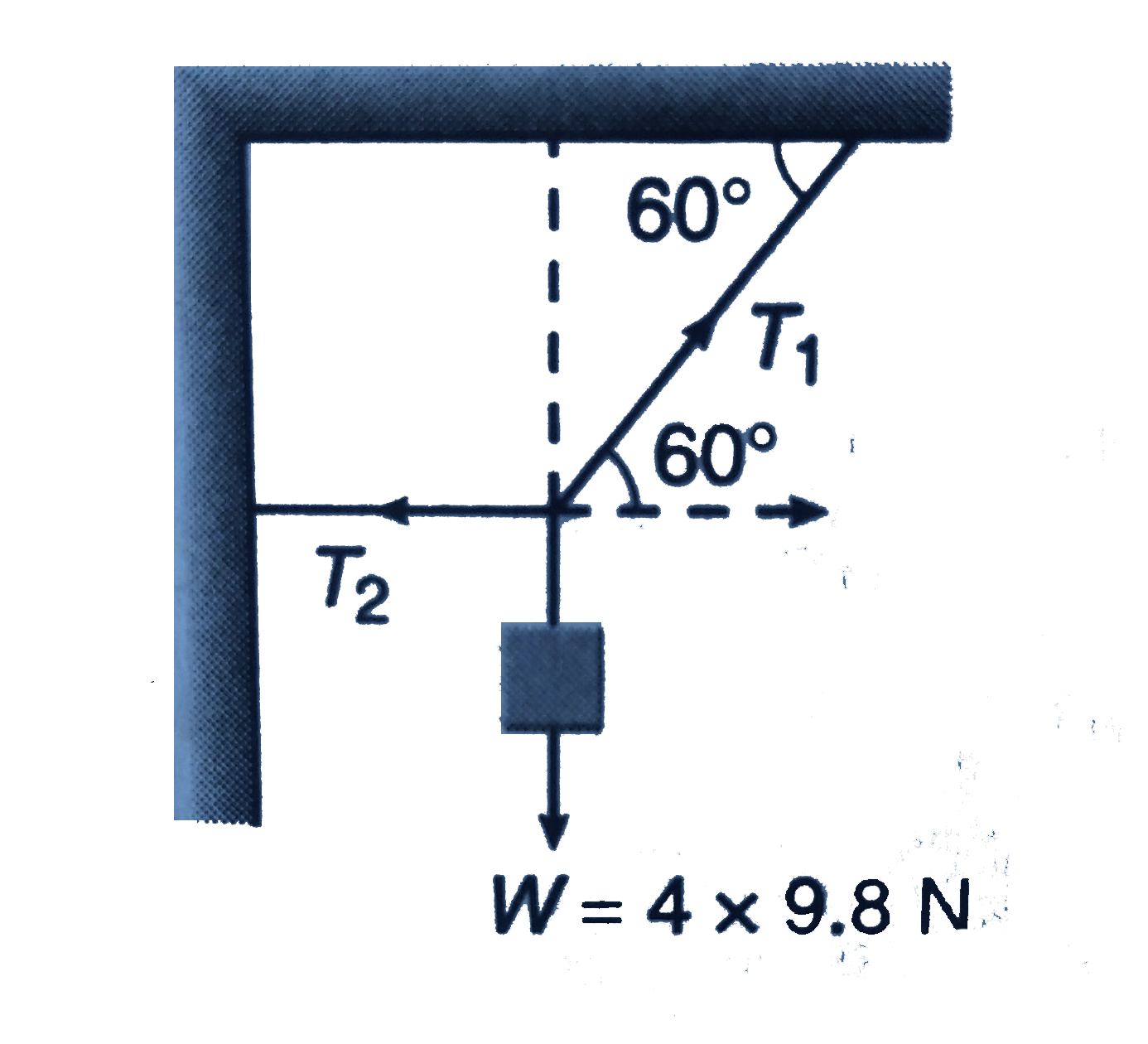
View Solution