A boy of mass 50 kg jumps with horizontal velocity of 1 m/s on to a stationary cart. If mass of the cart will be [Assume friction between the wheels the cart and road is zero ]
1011 m/s
1110 m/s
0⋅65 m/s
0⋅8 m/s
The correct Answer is:A
To solve the problem, we will use the principle of conservation of linear momentum.
1. Identify the masses and velocities:
- Mass of the boy, mb=50kg
- Initial horizontal velocity of the boy, vb=1m/s
- Mass of the cart, mc=5kg
- Initial velocity of the cart, vc=0m/s (since it is stationary)
2. Calculate the initial momentum of the system:
- The initial momentum Pi of the system (boy + cart) can be calculated as:
Pi=mb⋅vb+mc⋅vc
- Substituting the values:
Pi=(50kg⋅1m/s)+(5kg⋅0m/s)=50kg m/s
3. Set up the final momentum equation:
- After the boy jumps onto the cart, the total mass of the system is mb+mc=50kg+5kg=55kg.
- Let V be the final velocity of the boy and the cart together. The final momentum Pf is given by:
Pf=(mb+mc)⋅V=55kg⋅V
4. Apply the conservation of momentum:
- According to the conservation of momentum, the initial momentum equals the final momentum:
Pi=Pf
- Substituting the values we calculated:
50kg m/s=55kg⋅V
5. Solve for the final velocity V:
- Rearranging the equation to solve for V:
V=50kg m/s55kg=1011m/s
6. Conclusion:
- The final velocity of both the boy and the cart after the boy jumps onto the cart is V=1011m/s.
- Mass of the boy, mb=50kg
- Initial horizontal velocity of the boy, vb=1m/s
- Mass of the cart, mc=5kg
- Initial velocity of the cart, vc=0m/s (since it is stationary)
- The initial momentum Pi of the system (boy + cart) can be calculated as:
Pi=mb⋅vb+mc⋅vc
- Substituting the values:
Pi=(50kg⋅1m/s)+(5kg⋅0m/s)=50kg m/s
- After the boy jumps onto the cart, the total mass of the system is mb+mc=50kg+5kg=55kg.
- Let V be the final velocity of the boy and the cart together. The final momentum Pf is given by:
Pf=(mb+mc)⋅V=55kg⋅V
- According to the conservation of momentum, the initial momentum equals the final momentum:
Pi=Pf
- Substituting the values we calculated:
50kg m/s=55kg⋅V
- Rearranging the equation to solve for V:
V=50kg m/s55kg=1011m/s
- The final velocity of both the boy and the cart after the boy jumps onto the cart is V=1011m/s.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)33videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -C) objective type questions (More than one options are correct)7videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - TRY YOURSELF67videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
- BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)26videos
MAGNETISM AND MATTER
Similar Questions
(i) How much momentum will a dumb-bell of mass 10kg transfer to the floor if it falls a height of 80cm? Take its downward acceleration to be 10m/s2.
(b) A girl of mass 40kg running at a speed of 5m/s horizontally jumps onto a stationary cart with frictionless wheels. The mass of the cart is 3kg. What is her velocity as the cart starts moving?View SolutionFigure-2.85 shows a block B of mass m, cart C of mass M, and the coefficient of static between the block and the cart is μ. Neglect frictional between wheels and axles and the rotational effects of the wheels. Determine the minimum value of F which must be applied on B such that it will not slide.
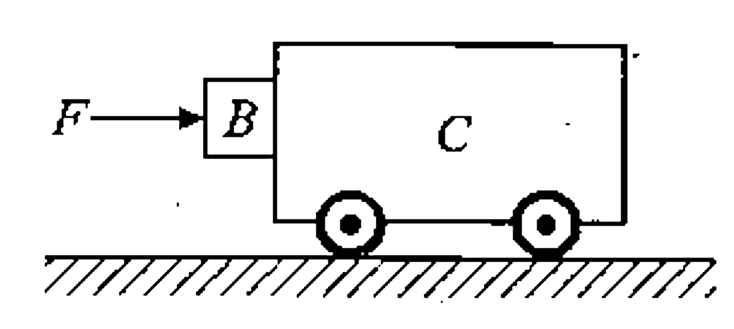
[mgμ(1+mM)]View Solution
Knowledge Check
- Question 1 - Select One
A girl of mass 40kg jumps with a horizontal velocity of 5m/s onto a stationary cart with frictionless wheels. The mass of the cart is 3kg. What is her velocity as the cart starts moving? Assume that there is no external unbalanced force working in the horizontal direction.
A100/43 m/sB200 m/sC200/43 m/sDNONE - Question 2 - Select One
Two carts of masses 200kg and 300kg on horizontal rails are pushed apart. Suppose the coefficient of friction between the carts and the rails are same. If the 200kg cart travels a distance of 36m and stops. Then the distance travelled by the cart weighing 300kg is : (if both have same initial speed)
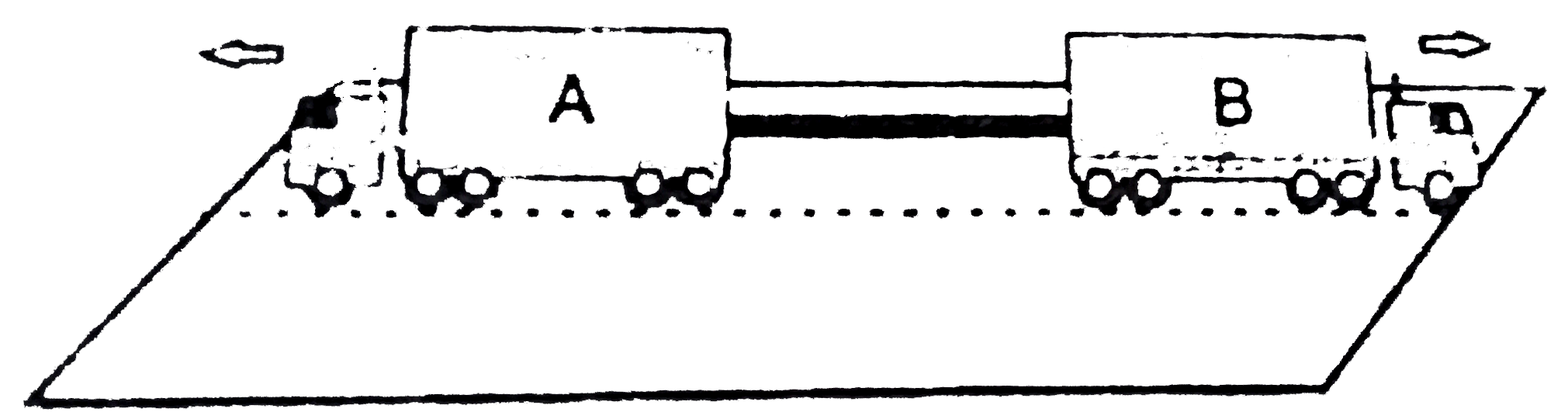 .A32 mB24 mC16 mD36 m
.A32 mB24 mC16 mD36 m - Question 3 - Select One
The block of mass m is in contact with a moving cart as shown in the figure.The coefficient of friction between the block and the cart is . The acceleration a of the cart that will prevent the block from falling is
 Aα≥gμBα<gμCα>mgμDα>gμm
Aα≥gμBα<gμCα>mgμDα>gμm
A rough inclined plane is placed on a cart moving with a constant velocity u on horizontal ground. A block of mass M rest on the incline. Is any work done by force of friction between the block and incline ? Is there then a dissipation of energy ?
View SolutionA child of mass 4kg jumps from cart B to cart A and then immediately back to cart B. The mass of each cart is 20kg and they are initially at rest. In both the cases the child jumps at 6m/s relative to the cart. If the cart moves along the same line with negligible friction with the final velocities of VB and VA, respectively, find the ratio of 6VB and 5VA.
 View Solution
View SolutionA cart loaded with sand moves along a horizontal plane due to a constant force F coinciding in direction with the cart's velocity vector. In the process, sand spills through a hole in the bottom with a constant velocity μkg/s. Find the acceleration and the velocity of the cart at the moment t, if at the initial moment t=0 the cart with loaded sand had the mass m0 and its velocity was equal to zero. The friction is to be neglected.
View SolutionA spring is compressed between two toy carts of mass m1 and m2. When the toy carts are released, the springs exert equal and opposite average forces for the same time on each toy cart. If v1 and v2 are the velocities of the toy carts and there is no friction between the toy carts and the ground, then :
View SolutionChoose the most appropriate option.
A block of mass mis in contact with the cart C as shown in the figure.
The coefficient of static friction between the block and the cart is u. The acceleration a of the cart that will prevent the block from falling satisfies.
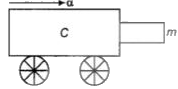 View Solution
View Solution

