A spring is compressed between two toy carts of mass m1 and m2. When the toy carts are released, the springs exert equal and opposite average forces for the same time on each toy cart. If v1 and v2 are the velocities of the toy carts and there is no friction between the toy carts and the ground, then :
v1/v2=m1/m2
v1/v2=m2/m1
v1/v2=m2/m1
V1/v2=m1/m2
To solve the problem, we will use the principle of conservation of momentum. The system consists of two toy carts with masses m1 and m2 that are initially at rest, and a spring that is compressed between them. When the spring is released, it exerts equal and opposite forces on both carts.
1. Identify Initial Conditions:
- Before the spring is released, both toy carts are at rest. Therefore, the initial momentum of the system is zero.
- Initial momentum, Pinitial=0.
2. Apply Conservation of Momentum:
- According to the law of conservation of momentum, the total momentum of a closed system remains constant if no external forces act on it.
- When the spring is released, the carts move away from each other with velocities v1 and v2.
- The final momentum of the system can be expressed as:
Pfinal=m1v1+m2v2
3. Set Up the Equation:
- Since the initial momentum is zero, we can set the final momentum equal to zero:
m1v1+m2v2=0
4. Rearranging the Equation:
- Rearranging gives us:
m1v1=−m2v2
- This indicates that the momentum gained by one cart is equal in magnitude and opposite in direction to the momentum gained by the other cart.
5. Express the Relationship:
- Dividing both sides by m1m2 gives:
v2v1=−m1m2
- Since we are interested in the magnitudes, we can ignore the negative sign (it indicates direction):
v2v1=m1m2
6. Final Relation:
- Thus, we can express the relationship as:
m1m2=v2v1
Conclusion:
The final relationship between the masses and velocities of the toy carts is given by:
m1m2=v2v1
- Before the spring is released, both toy carts are at rest. Therefore, the initial momentum of the system is zero.
- Initial momentum, Pinitial=0.
- According to the law of conservation of momentum, the total momentum of a closed system remains constant if no external forces act on it.
- When the spring is released, the carts move away from each other with velocities v1 and v2.
- The final momentum of the system can be expressed as:
Pfinal=m1v1+m2v2
- Since the initial momentum is zero, we can set the final momentum equal to zero:
m1v1+m2v2=0
- Rearranging gives us:
m1v1=−m2v2
- This indicates that the momentum gained by one cart is equal in magnitude and opposite in direction to the momentum gained by the other cart.
- Dividing both sides by m1m2 gives:
v2v1=−m1m2
- Since we are interested in the magnitudes, we can ignore the negative sign (it indicates direction):
v2v1=m1m2
- Thus, we can express the relationship as:
m1m2=v2v1
The final relationship between the masses and velocities of the toy carts is given by:
m1m2=v2v1
Topper's Solved these Questions
Similar Questions
A spring is compressed by a toy cart of mass 150g. On releasing the cart, it moves with a speed of 0.2m/s. Calculate the elastic potential energy of the spring.
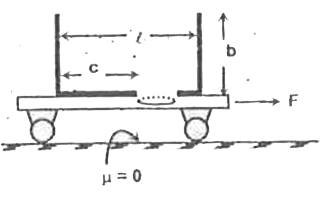
View SolutionA vessel with a hole in its bottom is fastened on a cart. The mass of the vessel and the cart is M and the area of the vessel base is A . What force F should the cart be puuled with so that maximum amount of water remains in the vessel ? The dimensions of the vessel are shown in the figure . Assume where is no friction between cart and ground and vessel is fixed with cart . ( ρ is density of water )
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A spring is compressed between two toy carts of masses m1 and m2. When the toy carts are released then spring exerts equal and opposite average force on each for the same time t. Assume that there is no friction between the toy carts and the ground, the velocities of toy carts are
AIn opposite directions but in inverse ratio of their massesBIn opposite directions but in direct ratio of their massesCEqual and in opposite directionDEqual and in same direction. - Question 2 - Select One
A spring is compressed between two toy carts to masses m1 and m2. When the toy carts are released, the spring exerts on each toy cart equal and opposite forces for the same small time t. If the coefficients of friction μ between the ground and the toy carts are equal, then the magnitude of displacements of the toy carts are in the ratio
A(a) S1S2=m2m1B(b) S1S2=m1m2C(c) S1S2=(m2m1)2D(d) S1S2=(m1m2)2 - Question 3 - Select One
A boy of mass 50 kg jumps with horizontal velocity of 1 m/s on to a stationary cart. If mass of the cart will be [Assume friction between the wheels the cart and road is zero ]
A1011 m/sB1110 m/sC0⋅65 m/sD0⋅8 m/s
Two carts (A & B) having spring bumpers collides as shown in figure. Initially v1≠0 & v2=0. When the separation between the carts is minimum.
 View Solution
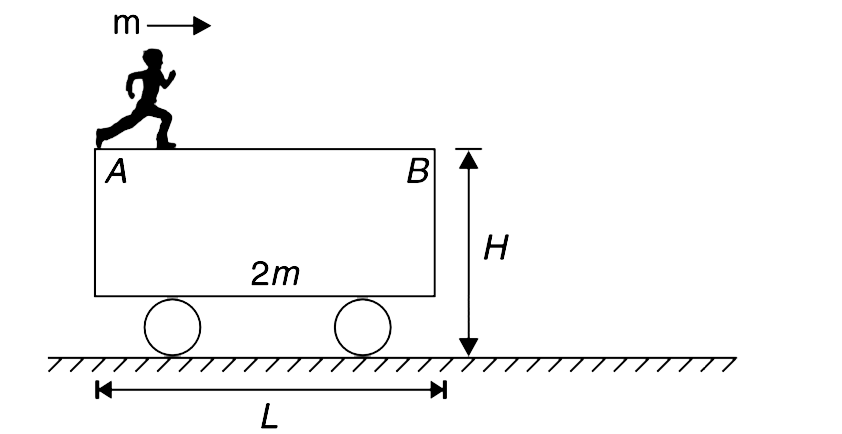
View SolutionA man of mass m is standing on the flat top of a cart of mass 2m. The length and height of the cart is LandH respectively and it is at rest on a smooth horizontal ground. The man starts running from end A, speeds up and jumps out of the cart at point B with a velocity u relative to the cart in horizontal direction. Calculate the total horizontal distance covered by the man by the time he lands on the ground.
 View Solution
View SolutionMomentum is the ability of imparting or tending to motion to other bodies. The total momentum of a system remains conserved if no external force is acting it. This is calculated by the formula, →p=m→v. Consider a situation where a cart carrying five boys is moving without friction due to inertia along a straight horizontal road, with a speed of 10m/s. After travelling certain distance, a boy jumps from the cart with a speed of 2m//s with respect to the cart in opposite direction to it. Then, second boy jumps with the same speed w.r.t. the cart, but in a perpendicular direction to the cart. The mass of the cart is 100 kg and mass of each boy is 20 kg.
If, in the first case, the second boy jumps out of the cart in a direction perpendicular to the motion of cart as seen from ground, then the speed ofView SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
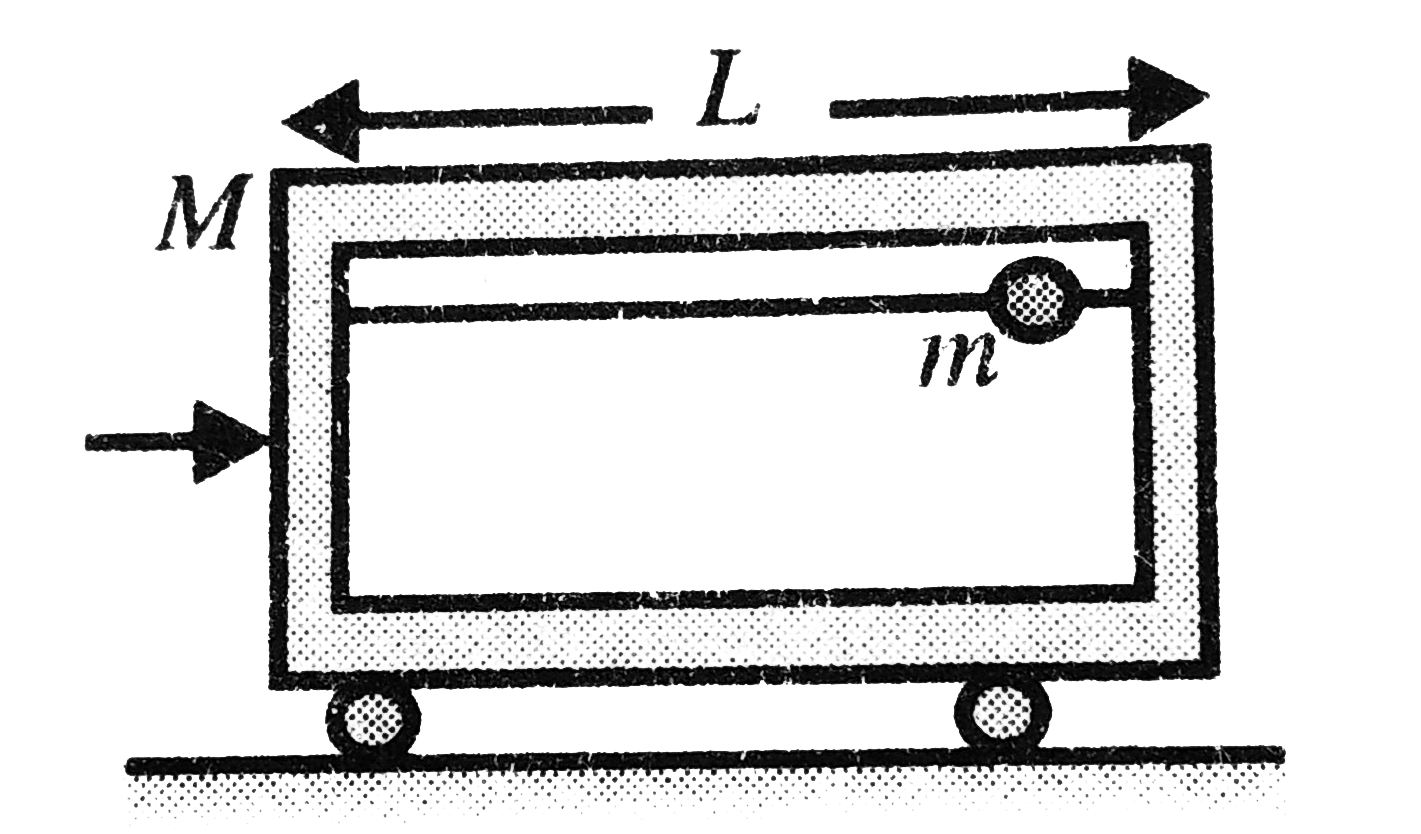
What is the velocity of the cart just after the first collision?View SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
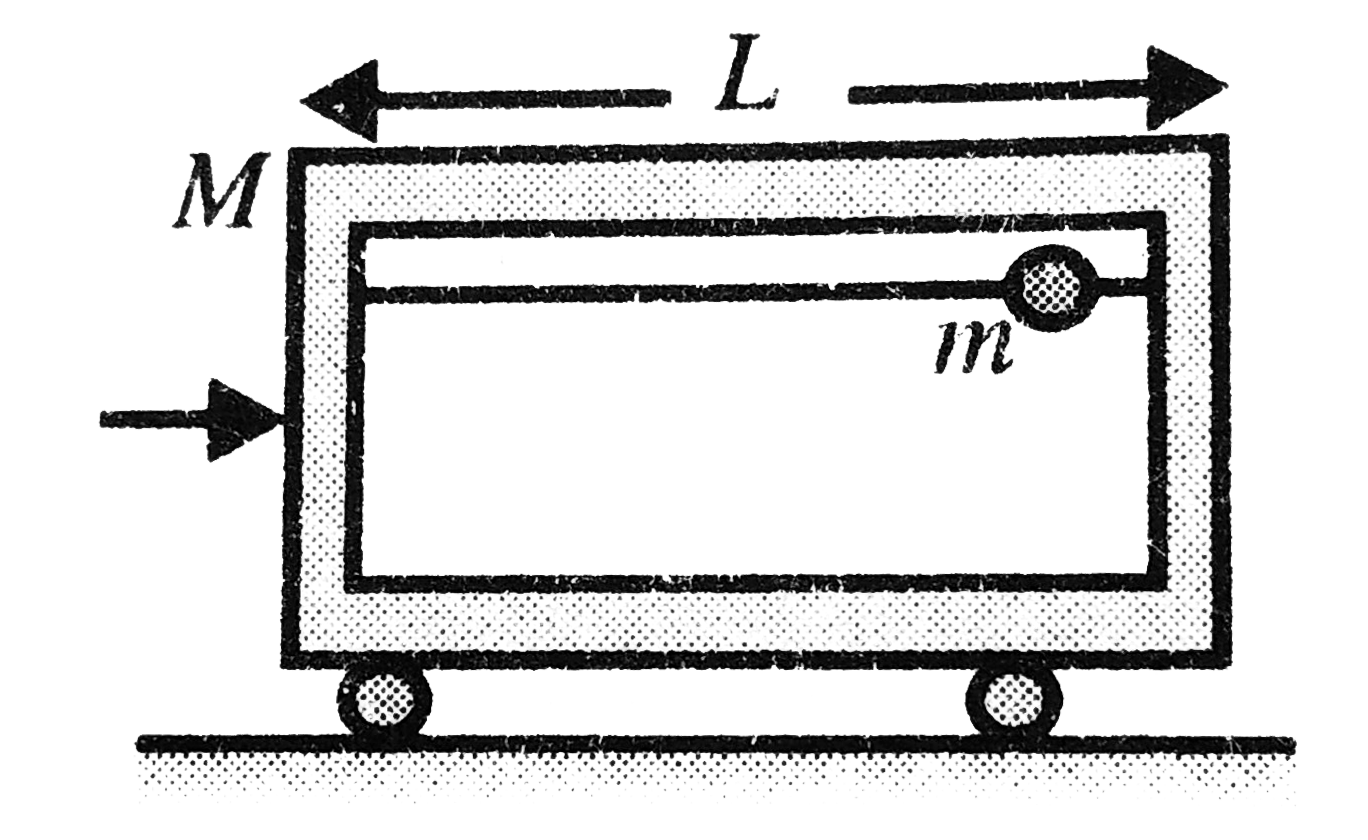
Velocity of bead just after the first collision isView Solution

