A uniformly charged disc of radius R with a total charge Q lies in the XY -plane. Find the electric field at a point at a point P, along the Z-a xis that passes through the centre of the discc perpendicular to its plane. Discuss the limit when $R > > z$ .
Strategy $:$ By treating the disc as a set of concentric uniformly charged rings, the problem could be solved by using the result obtained in example for ring. Consider a ring of radius of radius r' and thickness as shown in figure.

Text Solution

Verified by Experts

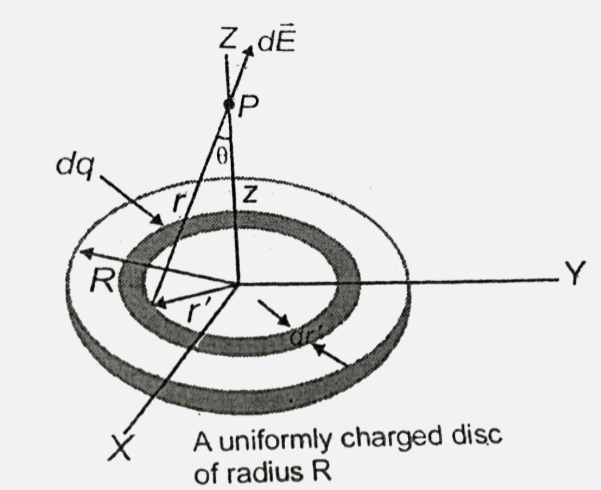
By symmetry arguments the electric field at P points in the $+ z$ direction . Since the ring has charge $d q = σ (2 π r' d r')$ , we see that the ring givesa contribution.

$d E_{z} = \frac{1}{4 π ε_{0}} \frac{z d q}{{(r^{' 2} + z^{2})}^{3 / 2}} = \frac{1}{4 π ε_{0}} \frac{z (2 π σ r' d r')}{{(r^{' 2} + z^{2})}^{3 / 2}}$
integrating from $' = 0$ to $r' = R$ the total electric fieldat P becomes.
$E_{z} = \int d E_{z} = \frac{σ z}{2 ε_{0}} \int_{0}^{R} \frac{r' d r'}{{(r^{' r} + z^{2})}^{3 / 2}} = \frac{σ z}{4 ε_{0}} \int_{z^{2}}^{R^{2} + z^{2}} \frac{d u}{u^{3 / 2}} = \frac{σ z}{4 ε_{0}} \frac{u^{- 1 / 2}}{(- 1 / 2)}) {∣ ∣ ∣ ∣}_{z^{2}}^{R^{+ z^{2}}}$
$= - \frac{σ z}{2 ε_{0}} [\frac{1}{\sqrt{R^{2} + z^{2}}} - \frac{1}{z}] = \frac{σ}{2 ε_{0}} [1 - \frac{z}{\sqrt{R^{2} + z^{2}}}]$
$\Rightarrow E_{z} = \frac{σ}{2 ε_{0}} [1 - \frac{z}{\sqrt{R^{2}} + z^{2}}]$
To show that the "point-charge" limit the recovered for $z > > R$ , we make use of the Binomial expansion
$1 - \frac{z}{\sqrt{z^{2} + R^{2}}} = 1 - {(1 - \frac{R^{2}}{z^{2}})}^{- 1 / 2} = 1 - (1 - \frac{1}{2} \frac{R^{2}}{z^{2}} + ... . .) = \frac{1}{2} \frac{R^{2}}{z^{2}}$
This gives
$E_{z} = \frac{σ}{2 ε} \frac{R^{2}}{z^{2}} = \frac{1}{4 π ε_{0}} \frac{σ π R^{2}}{z^{2}} = \frac{1}{4 π ε_{0}} \frac{Q}{z^{2}}$
which is indeed the expected "point-charge" result . On the other hand, we may also consider the limit where $R > > z$ . Physically this means that the plane is very large , or the field point P is extremely close to the surface of the plane. The electric field in this limit becomes,in unit-vector rotation.
$\to E = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} \frac{σ}{2 ε_{0}} ˆ k, & z > 0 - \frac{σ}{2 ε_{0}} ˆ k, & z > 0 \end{matrix}$

Updated on:21/07/2023