
CP ( without dielectric ) =2C
CQ ( without dielectric ) =C
k ad 2k the dielectric constant of two dielectric. Find resultant capacity between A and B
CAB=[K(2C)][2KC](k2C+2KC) = KC= kC
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT (SECTION-A) Objective Type Questions (Only one answer)
47 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions

Cp ( without dielectric ) = 2C
CQ ( without dielectric ) = C
k and 2 k are dielectric constant of two dielectrics . Find resultant capacity between A and B .
View Solution
Cp ( without dielectric ) = 2C
CQ ( without dielectric ) = C
k and 2 k are dielectric constant of two dielectrics . Find resultant capacity between A and B .
View Solution
Knowledge Check
The dielectric constant for H2O at 18∘C is
A22B82C28D88A parallel plate capacitor without any dielectric has capacitance C0. A dielectric slab is made up of two dielectric slabs of dielectric constants K and 2K and is of same dimensions as that of capacitor plates and both the parts are of equal dimensions arranged serially as shown. If this dielectric slab is introduced (dielectric K enters first) in between the plates at constant speed, then variation of capacitance with time will be best represented by :
 A
A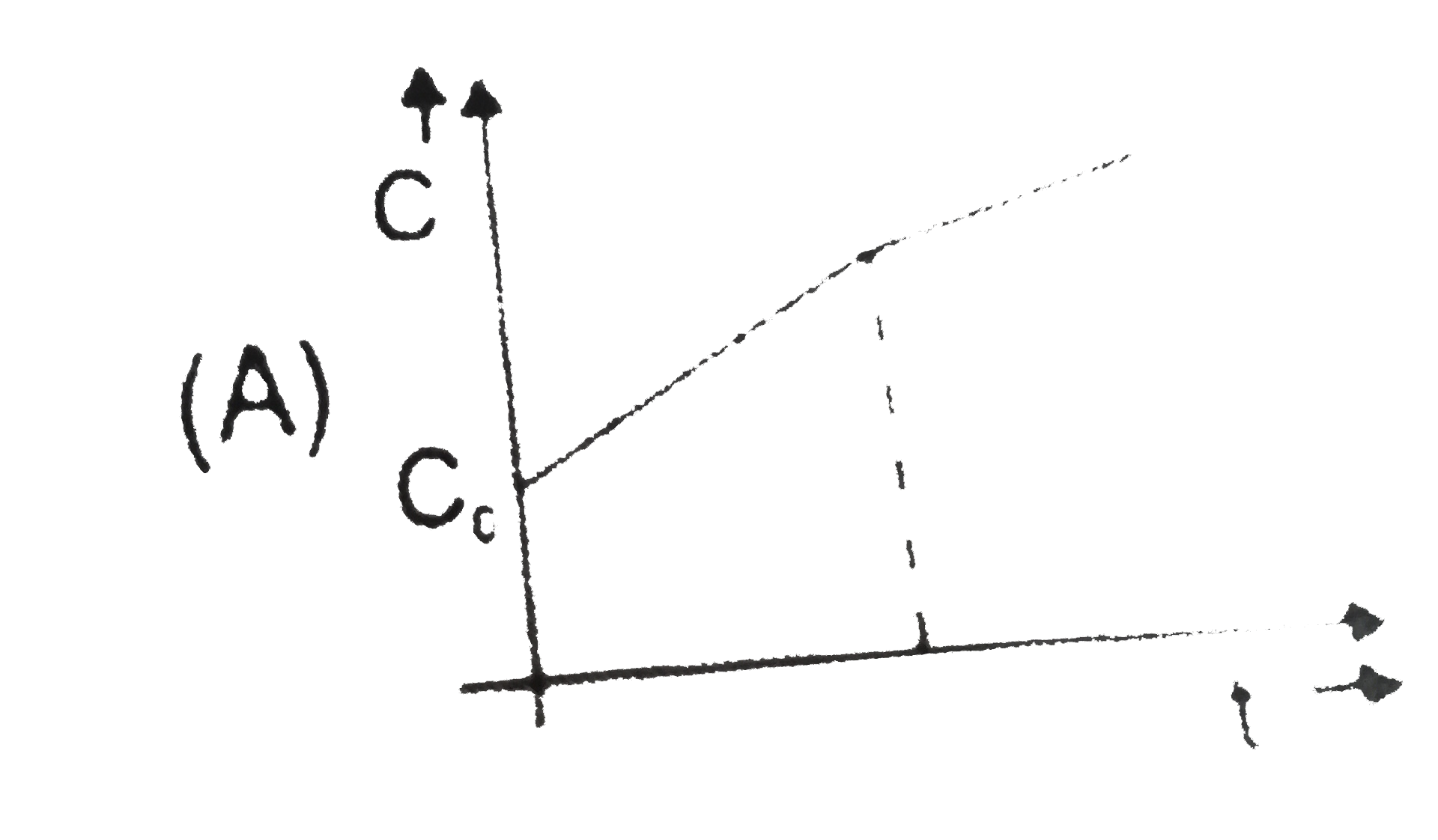 B
B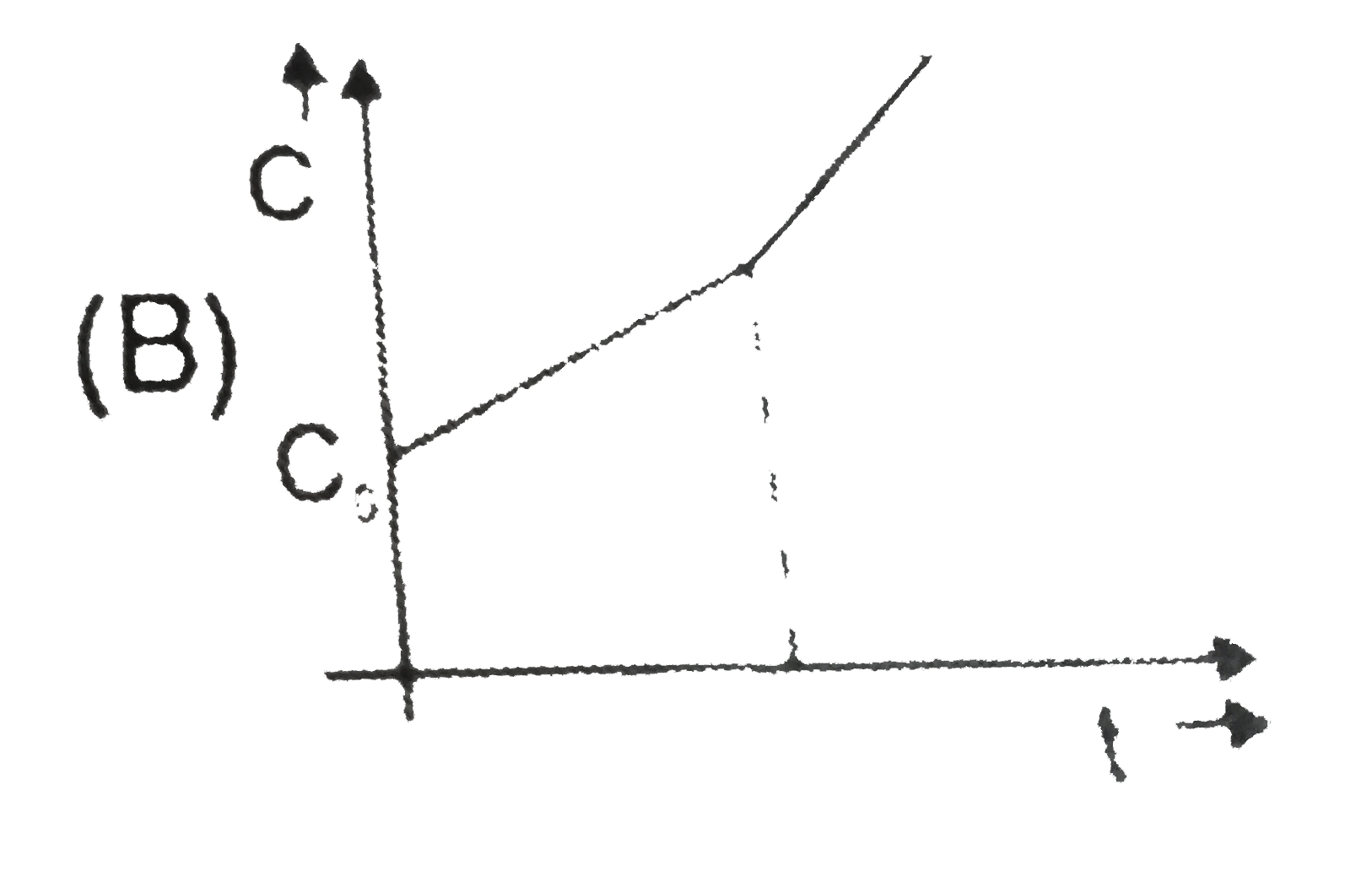 C
C D
D
The capacity of a condenser in which a dielectric of dielectric constant 5 has been used, is C. If the dielectric is replaced by another with dielectric constant 20, the capacity will become
A4CB2CCC2DC4
A parallel plate capacitor without any dielectric has capacitance C0. A dielectric slab is made up of two dielectric slabs of dielectric constants K and 2K and is of same dimensions as that of capacitor plates and both the parts are of equal dimensions arranged serially as shown. If this dielectric slab is introduced (dielectric K enters first) in between the plates at constant speed, then variation of capacitance with time will be best represented by :

View SolutionIf C and C0 are capacities of a capacitor with and " without dielectric medium respectively then dielectric constant of medium K is
View SolutionThree concentric conducting shells A,B and C of radii a,b and c are as shown in figure. A dielectric of dielectric constant K is filled between A and B. Find the capacitance between A and C.

View SolutionThree concentric conducting shells A,B and C of radii a,b and c are as shown in figure. A dielectric of dielectric constant K is filled between A and B. Find the capacitance between A and C.

View SolutionThe space between parallel plate capacitors is filled with four dielectrics of equal dimensions but of dielectric constants K1,K2,K3andK4 respectively. If K is the dielectric constant of a single dielectric that must be filled between capacitor plates to have the same capacitance between A and B. Then we must have

View Solution
