A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure. The new capacitance is C' . Then
![A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure. The new capacitance is C' . Then (1) C' C[(K)/(K+1)] (2) C' = C[(2K)/(K+1)] (3) C' =(2C )/( K+1) (4 ) C' =C[ (1)/(K)/(2)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/AAK_T5_PHY_C15_E01_037_Q01.png)
(1)
(2)
(3)
(4 )
Answer (2)

Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT (SECTION-A) Objective Type Questions (Only one answer)
47 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions
A paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View Solution
Knowledge Check
A paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then
 AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]
AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]A parallel plate capacitor has capacitance C. If it is equally filled with parallel layers of materials of dielectric constants K1 and K2 its capacity becomes C1. The ratio of C1→C is
AK1+K2BK1K2K1−K2CK1+K2K1K2D2K1K2K1+K2A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric (K=2), the percentage increase in the cpacitance will be
 A25%B50%C75%D100%
A25%B50%C75%D100%
A parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is

View SolutionAir filled capacitor of capacitance 2μF is filled with three dielectric material of dielectric constant K1=4,K2=4 and K3=6 as shown in the figure . The new capacitance of the capacitor is
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
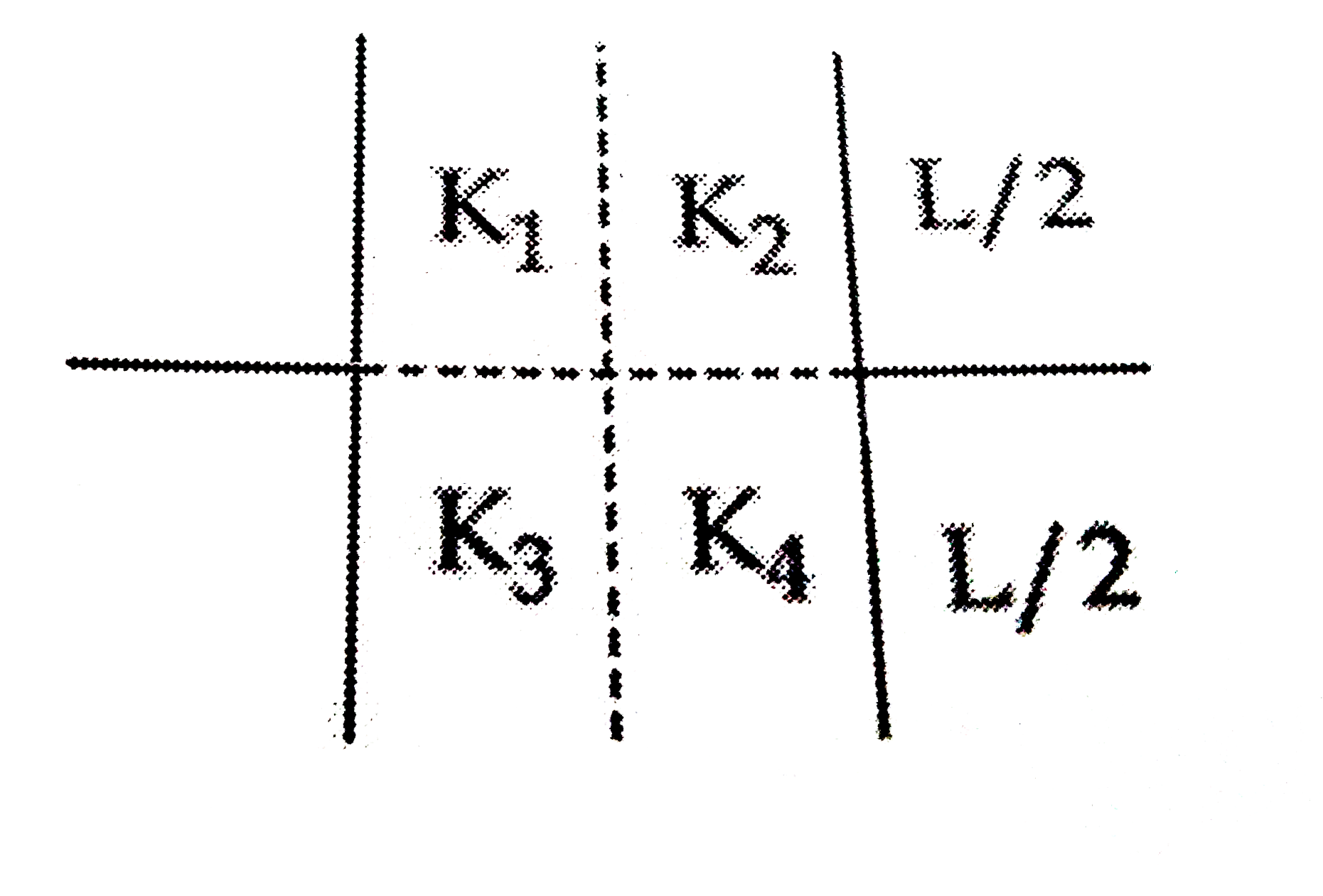
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionA parallel plate capacitor with oil as a dielectric between the plates has a capacitance C. if the oil, with dielectric constannt (K=3), is removed, then the capacitance of the capacitor will be
View Solution
