Air filled capacitor of capacitance 2μF is filled with three dielectric material of dielectric constant K1=4,K2=4 and K3=6 as shown in the figure . The new capacitance of the capacitor is
50μF
2μF
20μF
10μF
The correct Answer is:4
To find the new capacitance of the capacitor filled with three dielectric materials, we can follow these steps:
Step 1: Understand the Initial Conditions
The initial capacitance of the air-filled capacitor is given as:
C0=2μF
Step 2: Identify the Dielectric Constants
The dielectric constants for the three materials are:
- K1=4
- K2=4
- K3=6
Step 3: Calculate the Equivalent Dielectric Constant
When multiple dielectrics are present, the equivalent dielectric constant Keq can be calculated based on how the dielectrics are arranged (series or parallel). Assuming they are arranged in series, the formula for the equivalent dielectric constant is:
1Keq=1K1+1K2+1K3
Substituting the values:
1Keq=14+14+16
Step 4: Calculate Each Term
Calculating each term:
14=0.25,14=0.25,16≈0.1667
Adding these values together:
1Keq=0.25+0.25+0.1667=0.6667
Step 5: Find the Equivalent Dielectric Constant
Taking the reciprocal to find Keq:
Keq≈10.6667≈1.5
Step 6: Calculate the New Capacitance
The new capacitance C can be calculated using the formula:
C=Keq⋅C0
Substituting the values:
C=1.5⋅2μF=3μF
Step 7: Conclusion
The new capacitance of the capacitor after filling it with the three dielectric materials is:
C=3μF
The initial capacitance of the air-filled capacitor is given as:
C0=2μF
The dielectric constants for the three materials are:
- K1=4
- K2=4
- K3=6
When multiple dielectrics are present, the equivalent dielectric constant Keq can be calculated based on how the dielectrics are arranged (series or parallel). Assuming they are arranged in series, the formula for the equivalent dielectric constant is:
1Keq=1K1+1K2+1K3
1Keq=14+14+16
Calculating each term:
14=0.25,14=0.25,16≈0.1667
1Keq=0.25+0.25+0.1667=0.6667
Taking the reciprocal to find Keq:
Keq≈10.6667≈1.5
The new capacitance C can be calculated using the formula:
C=Keq⋅C0
Substituting the values:
C=1.5⋅2μF=3μF
The new capacitance of the capacitor after filling it with the three dielectric materials is:
C=3μF
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
An air capacitor of capacitance C plate area A and plate separation d has been filled with three dielectrics of constant k1=3,k2=6 and k3=4 as shown in figure . What is the new capacitance ?

View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1, k2 and k3 as shown. If a isngle dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
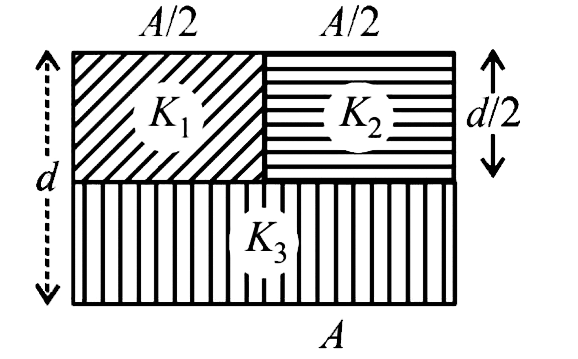
View SolutionA paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then

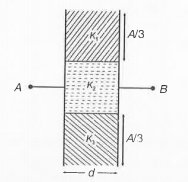
View SolutionA parallel plate capacitor of plate area A and separation d filled with three dielectric materials as show in figure. The dielectric constants are K1, K2 and K3 respectively. The capacitance across AB will be :
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
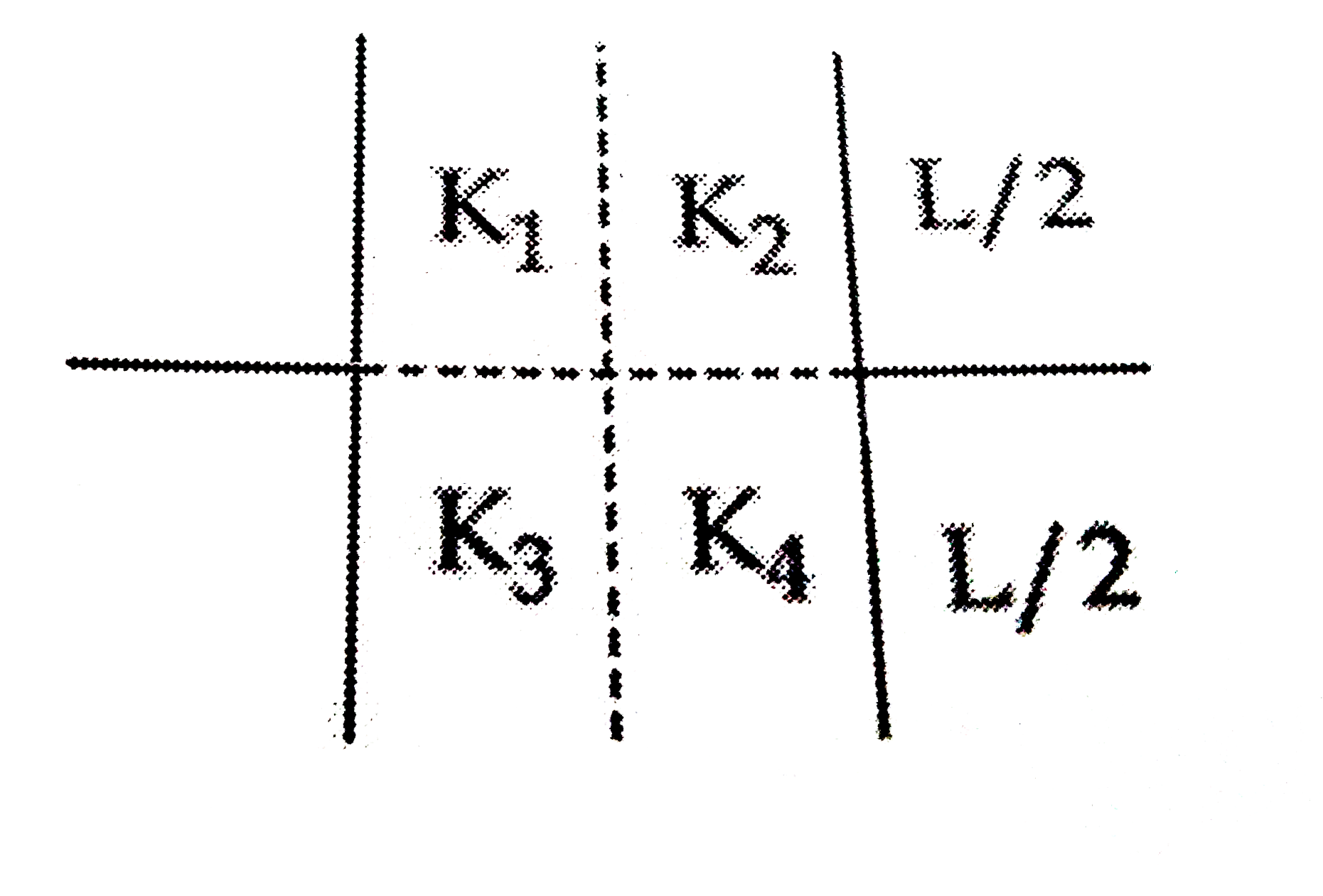
View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

View SolutionThe space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical size as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.

View SolutionConsider a parallel plate capacitor of 10μF (micro-farad) with air filled in the gap between the plates. Now one half of the space between the plates is filled with a dielectric of dielectric constant 4, as shown in the figure. The capacity of the capacitor charges to

View Solution
