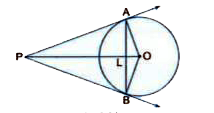
In the given figure AB is a chord of a circle, with centre O, such that AB=16cm and radius of circle is 10 cm. Tangent at A and B intersect each order at P. Find the length of PA.
AB=16cm
AL=AB/2=8cm
In ∠OAL
AL2+OL2=OA2
So we get, OL=6cm
Hence,tan(θ)=OAPA=OLAL
(PA)=(OA)⋅ALOL
Therefore, PA=80/6=40/3.
Similar Questions
In Fig , AB is a chord of a circle , with centre O , such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P . Find the length of PA.
View SolutionIn the given figure, AB is a chord of a circle with centre O such that AB=16cm and radius of the circle is 10 cm. Tangent at A and B intersect each other at P. Find PA.
View SolutionIn the figure above, O is the centre of the circle CD is a tangent to the circle at E. OE bisects the chord AB at F. AB = 16 cm and EF = 2 cm. Find the length of DE (in cm).

View SolutionIn a circle of radius 4 cm a chord AB of length 4 cm is drawn. PA and PB are tangents to the circle then find /_APB .
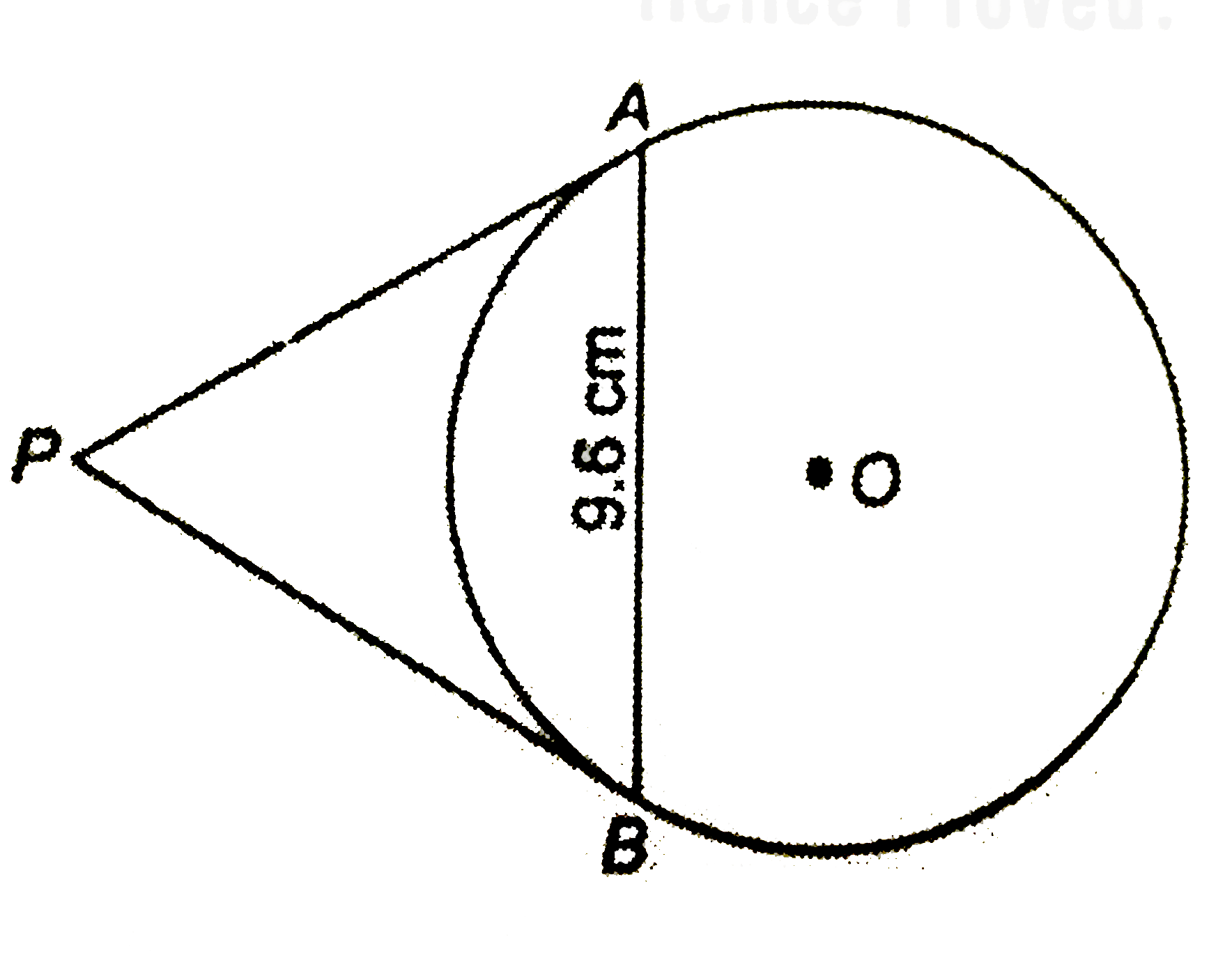
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
View SolutionAB is a chord of a circle with centre at O and radius 13 cm in length If AB = 10cm then find the distance from centre to the chord.
View SolutionA chord AB of length 16 cm is drawn in a circle of diameter 20 cm. If tangents at A and B intersect each other at point P, find the length of PA.
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB = 15 cm, PB = 9 cm, then find the length of PD.
View Solution
