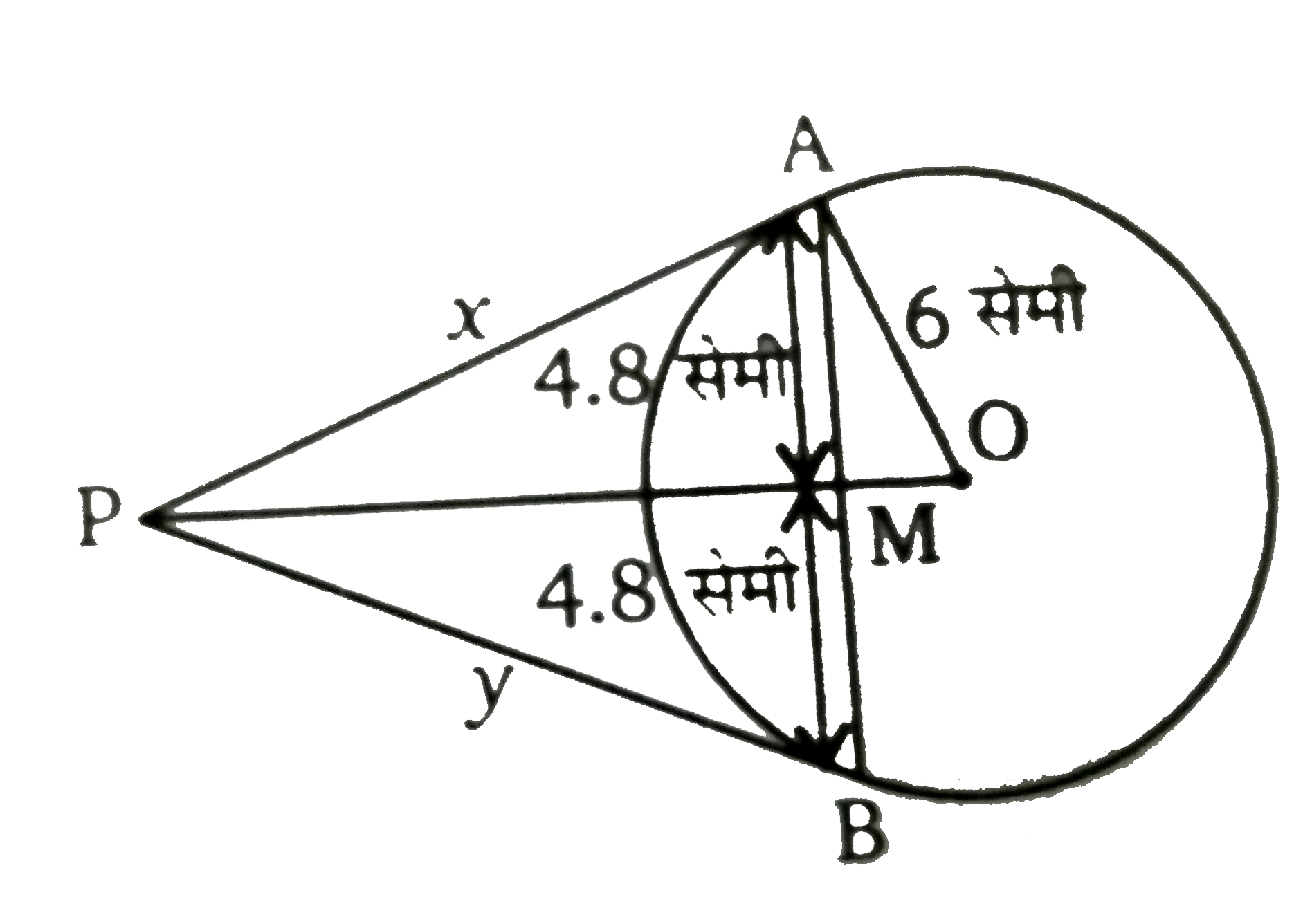
संलग्न चित्र में O केन्द्र तथा 6 सेमी त्रिज्या वाले एक वृत्त की जीवा की लम्बाई 9.6 सेमी है। A व B पर स्पर्शी, बिन्दु P पर परस्पर प्रतिच्छेद करती है। PA की लम्बाई ज्ञात कीजिए ।

Video Solution

Text Solution

Verified by Experts

OP व OA को मिलायें ।
हम जानते हैं कि बाह्य बिन्दु से वृत्त पर डाली गयी स्पर्शी बराबर होती है, इसलिए PA = PB
OP कोण $∠ A P B$ का लम्बअर्द्धक है।
$∵ O P, A B$ के लंबवत है तथा OP, AM को बिन्दु M पर प्रतिछेद करता है।
इसलिए $A M = M B = \frac{9.6}{2} = 4.8$ सेमी
$∵$ स्पर्श बिन्दु पर स्पर्श रेखा, त्रिज्या के लंबवत होती है।
$∠ O A P = 90^{\circ}$
अब समकोण त्रिभुज AMO में OA = 6 सेमी AM = 4.8 सेमी
$O M = \sqrt{{(O A)}^{2} - {(A M)}^{2}} = \sqrt{{(6)}^{2} - {(4.8)}^{2}} = 3.6$ सेमी
पाइथागोरस के प्रमेय से $Δ A M P$ में $x^{2} = y^{2} + {(4.8)}^{2}$
तथा पाइथागोरस प्रमेय से $Δ P A O$ में $O P^{2} = P A^{2} O A^{2}$
$\Rightarrow {(y + 3.6)}^{2} = x^{2} + 6^{2}$
$\Rightarrow y^{2} + {(3.6)}^{2} 92 y (3.6) = x^{2} + 36 = [y^{2} + {(4.8)}^{2}] + 36$
$\Rightarrow 7.2 y = {(4.8)}^{2} - {(3.6)}^{2} + 36 \Rightarrow y = 64$ सेमी
यह मान निम्न संबंध में प्रयोग करने पर
$x^{2} = y^{2} + {(4.8)}^{2} = {(6.4)}^{2} + {(4.8)}^{2} = 40.96 + 23.04 = 64$
$\Rightarrow x = 8$ सेमी अतः PA = 8 सेमी

Updated on:21/07/2023

|

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-वृत्त -स्वमूल्यांकन परीक्षण

Home
Ask Doubt
Profile