Molecule of a gas in a container hits one wall (1) normally and rebounds back. It suffers number of collision and hits the opposite wall (2) which is at angle of 30∘ with wall 1. Assuming the collision to be elastic and the small collision time to be the same for both the walls. The magnitude of average force by walls and 2 are F1 and F2 provide to molecule during collision satisfy
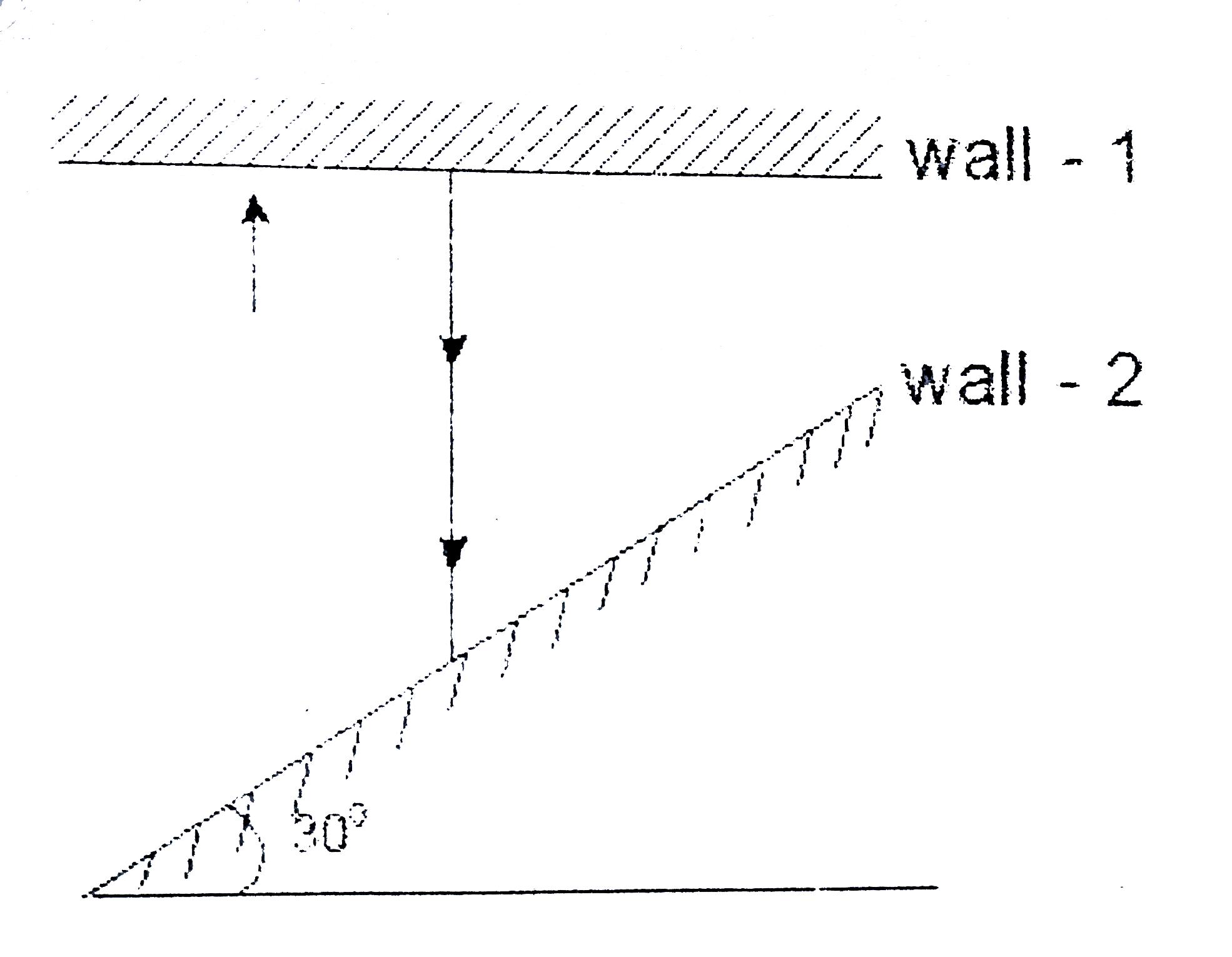
F1>F2
F1<F2
F1=F2 both non zero
F12F220
The correct Answer is:A
F1=2mvΔt F2=2mvcos30∘Δt
Hence F1>F2
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A smooth ball hits a smooth wall at a certain angle. The collision is elastic. Prove that the angle of reflection is equal to the angle of incidence.
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
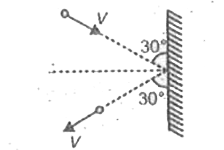
View Solution
Knowledge Check
If gas molecules undergo, inelastic collision with the walls of the container
AThe temperature of the gas will decreaseBthe pressure of the gas will increaseCneigher the temperature nor the presure will changeDThe temperature of the gas will increaseThe collisions between the molecules among themselves and with walls of a container are
Aperfectly elastic in which only momentum is conservedBperfectly elastic in which momentum and energy both are conservedCperfectly elastic in which momentum energy and velocity is conservedDresponsible for P.E. of gasA molecule of mass m moving at a velocity v impinges elastically on the wall at an angle a with the wall. Then
Athe impulsive reaction of the wall is 2mvcosαBthe impulsive reaction of the wall is 2mvsinαCthe impulsive reaction of the wall is nonzeroDgiven data is insufficient to calculate impulsive reaction of the wall
A molecules in a gas container hits the wall with speed 200m/s at an angle 30∘ with the normal, and reboudns with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
View SolutionIf a ball strikes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
View SolutionA molecule of mass 'm' collide with a wall of container in normal direction with a velocity c. if the collision is perfectly elastic, then the change in momentum of the molcules is
View SolutionWhat is the average horizontal force acting on a ball when it elestically bounces off a wall, assuming the collision times is 0.1 s and the momentum of the ball before the the bounce was 2kg. m/s, perpendicular to the wall ?
View SolutionConsider the situation as shown in the diagram , the ball strikes the wall normally and the collision is elastic , the change in the kinetic energy of the ball is
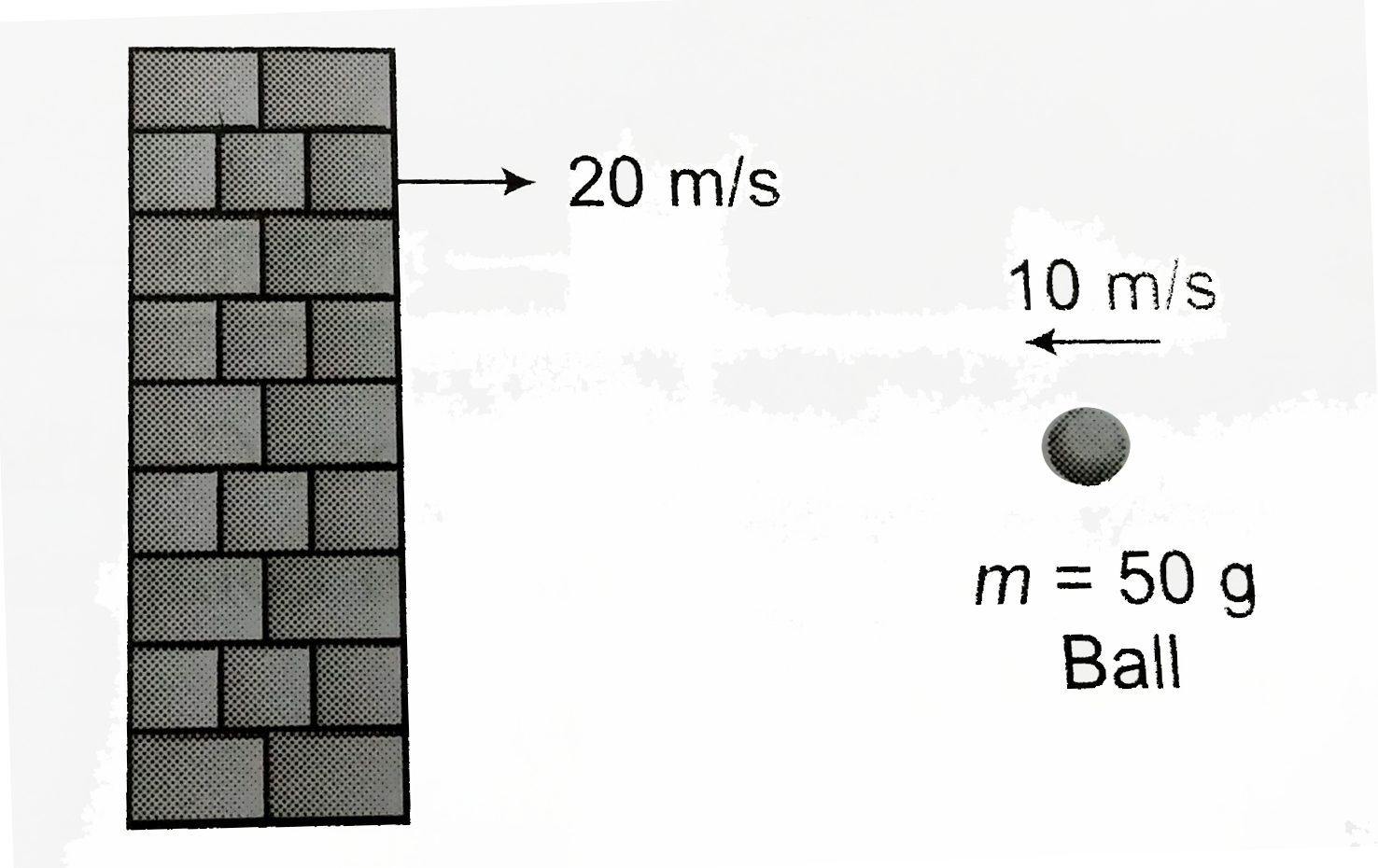
View Solution
