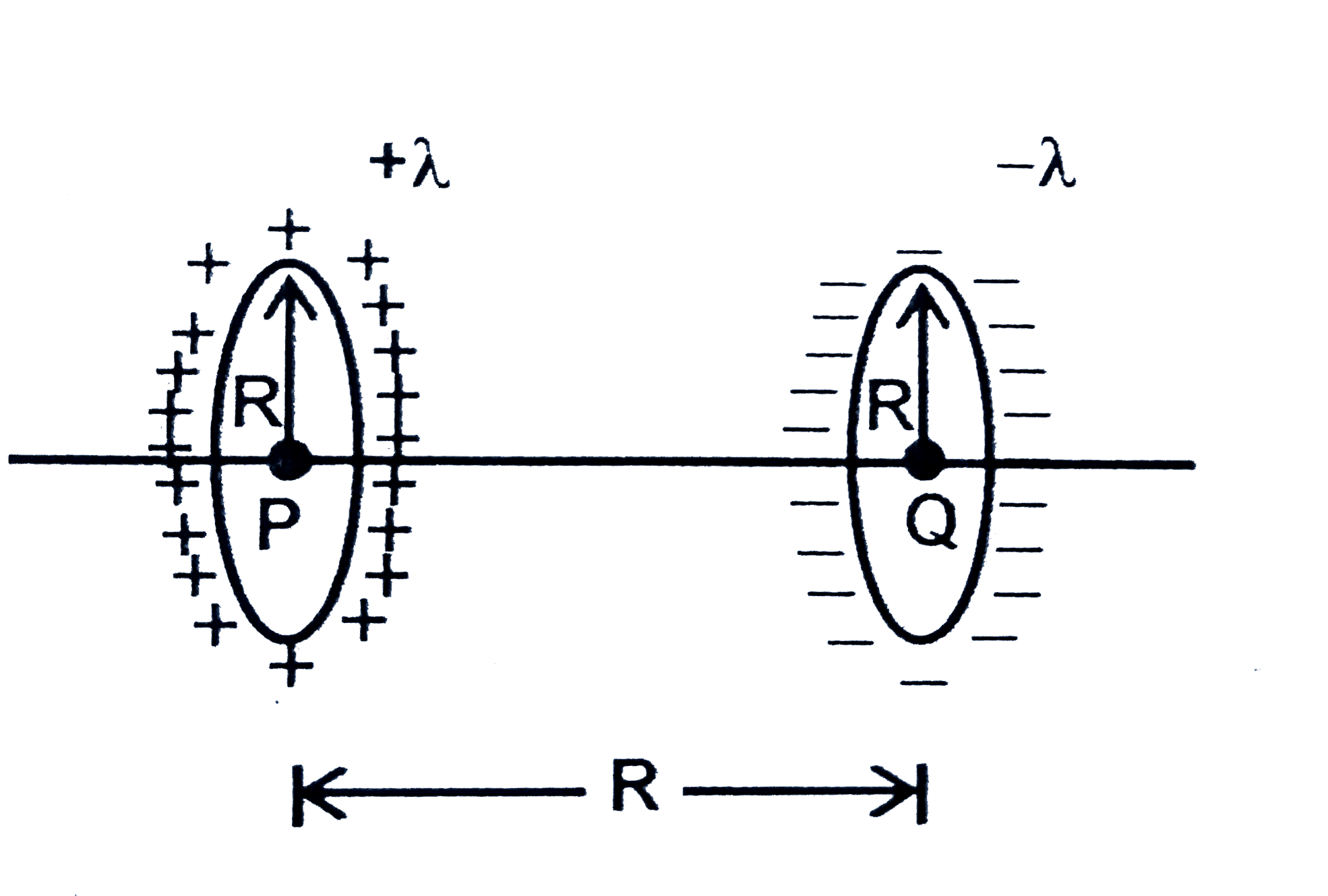
Two fixed insulating rings A and B carry ahanges with uniform linear aharge density +λ and −λ, respectively, as shown in the adjacent figure. The planes of the rings are parallel to each other and their axes are coinciding. A particle of change "q" and mass "m" is released with zero velocity from centre P of the positively charged ring. The kinetic energy of the particle when it reaches centre Q of the negatively charge ring will be
⎷2λqm∈0(1−1√2)
λ∈0(1−1√2)q
λ2∈0(1−1√2)q
none of these
The correct Answer is:B
Potential at P due to rings
VP=λ2πR4π∈0R−λ2πR4π∈0√2R=λ2∈0(1−1√2)
Potential at Q due to rings is
VQ=−λ2∈0(1−1√2)
Δ(K.E.)+(VQ−VP)q=0
⇒12mv2=λ∈0(1−1√2)q
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Knowledge Check
An electron released on the axis of a positively charged ring at a large distance from the centre will
ANot moveBDo oscillatory motionCDo SHMDDo non-periodic motionA rod with linear charge density λ is bent in the shap of circular ring. The electric potential at the centre of the circular ring is
Aλε0Bλ2ε0Cλε0D2λε0Two identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
AQq4πε0RBQq2πε0R)CQq8πε0RD3Qq4πε0R
A point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.

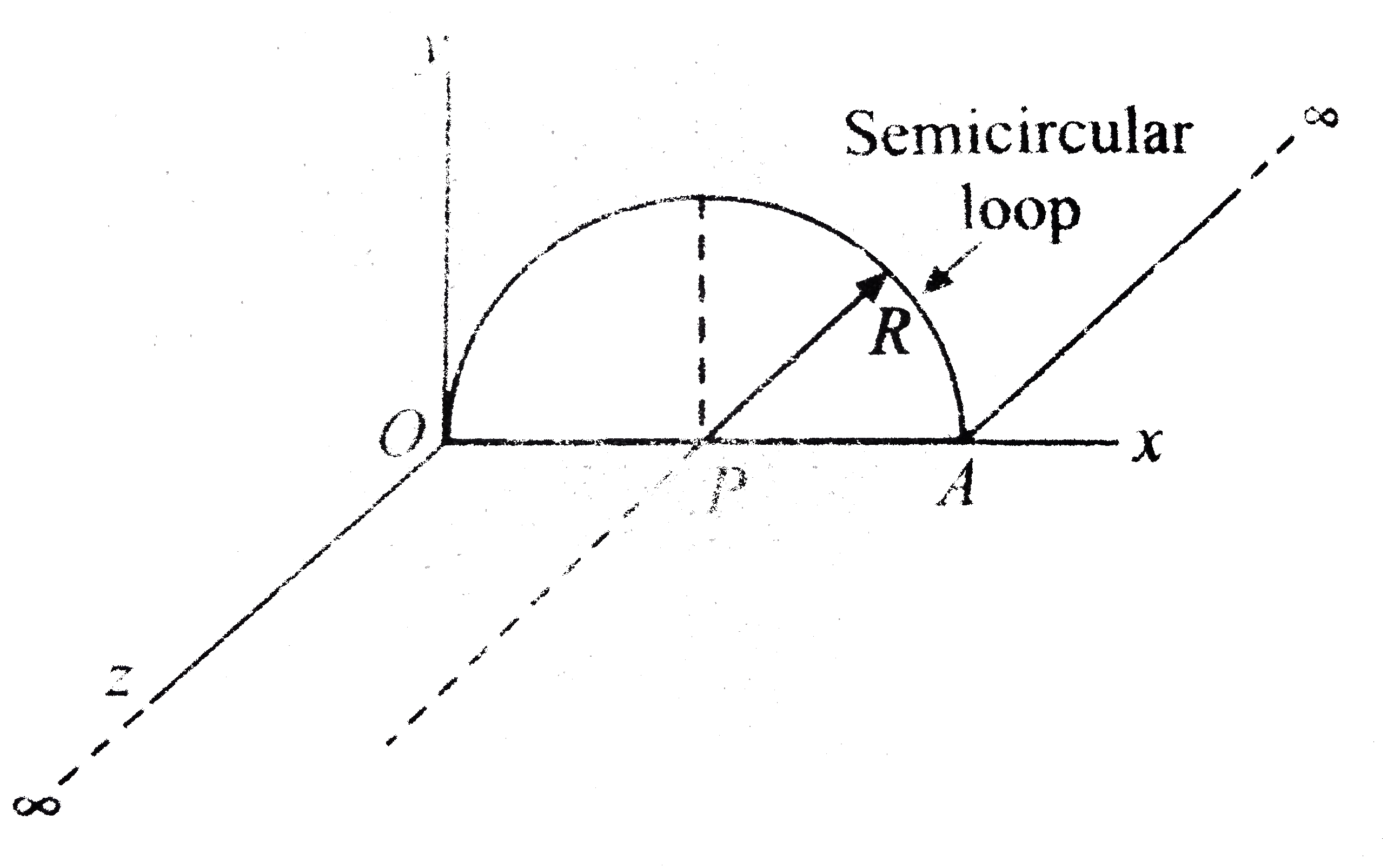
View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
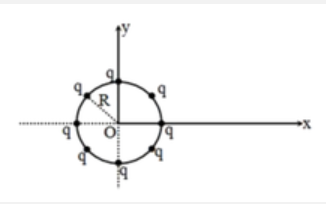
View SolutionEight charges each of value q are placed on a ring of radius R placed in x - y plane with origin at centre . A - q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v . The velocity of - q when it reaches the centre of ring is (neglect gravity)
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
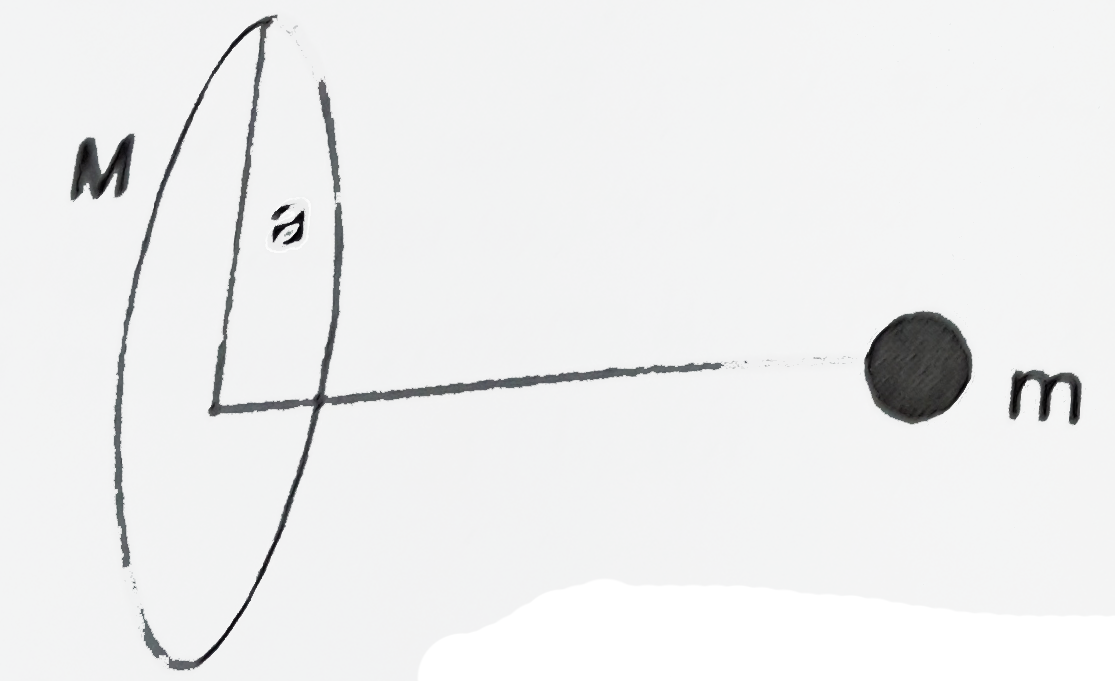
The force, when x=0 :
View SolutionEight charges each of value q each are placed on a ring of radius R placed in x-y plane with origin at centre -q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v. The velocity of -q when it reaches the centre of ring is (neglect gravity)-

View Solution
