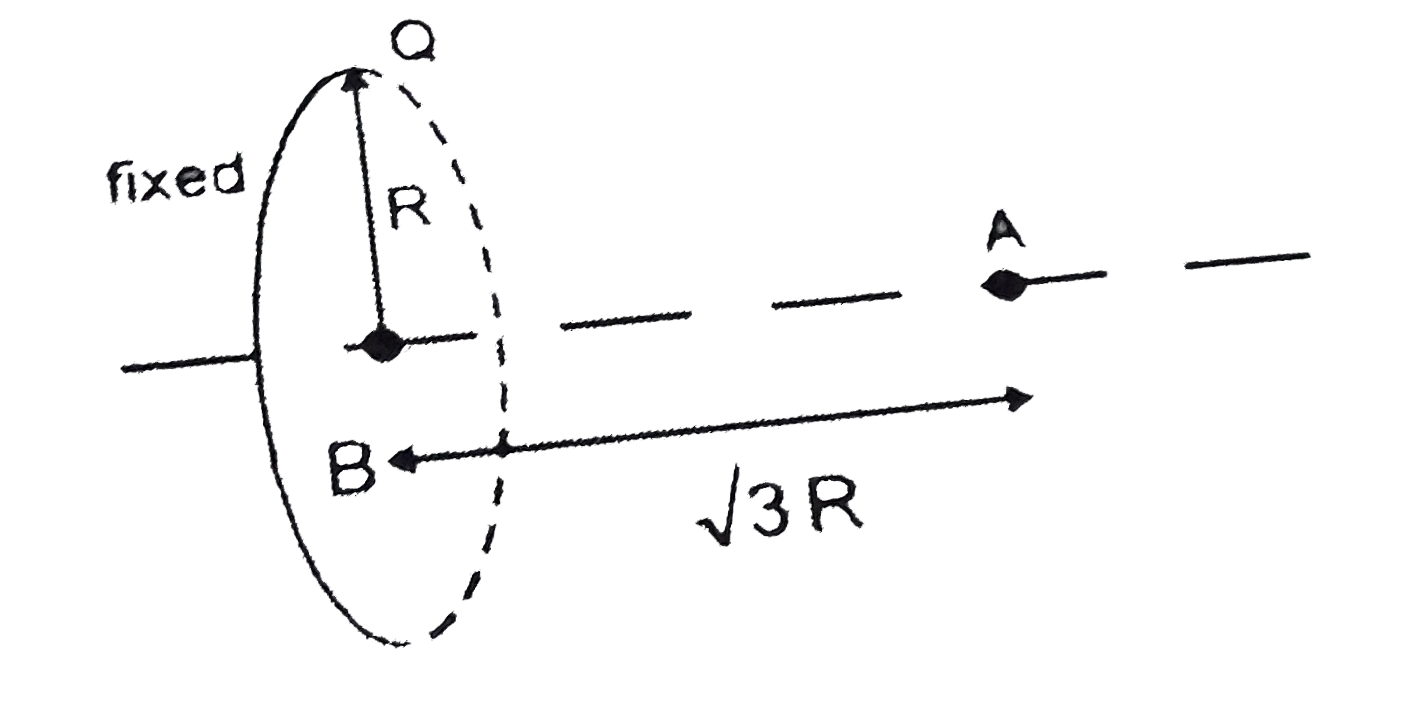
A point charge of charge -q and mass m is released with negligible speed from a distance $\sqrt{3} R$ on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.

Video Solution

Text Solution

Verified by Experts

As potential due to uniformly charged ring at its axis (at x distance) is :
$V = \frac{k Q}{\sqrt{R^{2} + x^{2}}}$ ,
So, potential at point a due to ring
$V_{1} = \frac{k Q}{\sqrt{R^{2} + 3 R^{2}}} = \frac{k Q}{2 R}$
So potential energy of charge -q at point A
$P . E ._{1} = \frac{- k Q q}{2 R}$ and potential at point B, $V_{2} = \frac{k Q}{R}$
So, potential energy of charge -q at point $B : P . E ._{2} = \frac{- k Q q}{R}$
Now by energy conservation : $P . E ._{1} + K . E ._{1} = P . E ._{2} + K . E_{2}$
$\frac{- k Q q}{2 R} + 0 = \frac{- k Q q}{R} + \frac{1}{2} m v^{2} \Rightarrow v^{2} = \frac{k Q q}{m R}$
So velocity of charge $- q$ at point $B v = \sqrt{\frac{k Q q}{m R}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
A $\frac{1}{4 π ε_{0}} \frac{q}{3 \sqrt{3} R^{2}}$
B $\frac{1}{4 π ε_{0}} \frac{2 q}{3 R^{2}}$
C $\frac{1}{4 π ε_{0}} \frac{2 q}{3 \sqrt{3} R^{2}}$
D $\frac{1}{4 π ε_{0}} \frac{3 q}{2 \sqrt{2} R^{2}}$
Question 2 - Select One
The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance $r$ from the centre
A $\frac{Q}{4 π ε_{0} r}$ for points outside and $\frac{Q}{4 π ε_{0} R}$ for points inside the shell
B $\frac{Q}{4 π ε_{0} e}$ for both points inside nad outside the shell
Czero for points outside and $\frac{Q}{4 π ε_{0} r}$ for points inside the shell
Dzero for both points inside and outside the shell
Question 3 - Select One
A positive charge $Q$ is uniformly distrubuted along a circular ring of radius $R$ .a small test chage $q$ is placed at the centre of the ring .The

Aif $q > 0$ and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.
Bif $q < 0$ and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.
Cif $q < 0$ it will perform $S H M$ for small displacement along the axis
D $q$ at the centre of the ring is in an unstable equilibrium within the plane of the ring for $q < 0$

RESONANCE-ELECTROSTATICS-Problems

Home
Ask Doubt
Profile