A uniform rod lies at rest on a frictionless horizontal surface. A particle, having a mass equal to that of the rod, moves on the surface perpendicular to the rod collides with it, and finally sticks to it. The minimum loss of KE in the collision , under the given conditions, is
5%
10%
20%
30%
The correct Answer is:C
The maximum loss occurs when the collision is "head-on" and the minimum is when it collides at a an end. Assume that the particle strikes the rod (of length 2L ) perpendicularly at a distance x from its centre. Apply conservation of momentum and angular momentum to calculate the final velocity of the rod and also its angular velocity. The fractional loss in KE=1/[3(x/L)2+2]

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.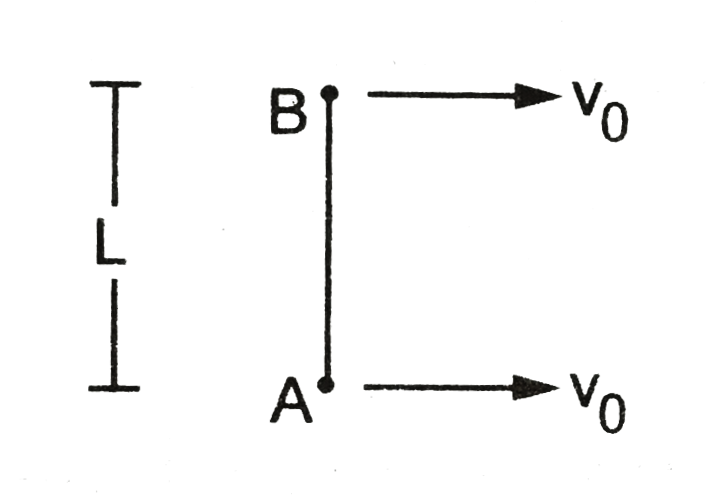
View Solution
Knowledge Check
A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
 AFB3FC5F4D7F4
AFB3FC5F4D7F4
A thin, uniform rod of mass M and length L is at rest on a smooth horizontal surface. A particle of same mass M collides with the rod at one end perpendicular to its length with velocity V∘ and sticks to it. C is the middle point of the rod and D is a point at a distance of L/4 from end A. the time taken by the rod turn through 90∘ after collisions.ALV∘BπLV∘C3πL5V∘D5πL12V∘A uniform metallic rod lies on a smooth horizontal surface. C is centre of mass of rod and A is a point on the rod. As the temperature increase
AC moves to the right and A remains at the same position.
 BC moves to the left and A moves to the right.CA moves to the right and C remains at the same position.DA & C both remains at the same position
BC moves to the left and A moves to the right.CA moves to the right and C remains at the same position.DA & C both remains at the same position
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA uniform rod is resting freely over a smooth horizontal plane. A particle moving horizontally strikes at one end of the rod normally and gets stuck. Then
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View SolutionTwo small balls A and B, each of mass m, are joined rigidly at the ends of a light rod of length L. They are placed on a frictionless horizontal surface. Another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown in the figure. If the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be
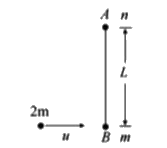
View Solution
