A positively aharged particel (q,m) enters in a uniform magnetic field 'B' at an angle of 60∘ as shown in figure with speed vo. Collision between the charge particle and the wall is perfectly elastic. Then find the time in which the charge particel comes out from the magnetic field.
⎛⎜
⎜⎝taked=(√3−1)mv2qB⎞⎟
⎟⎠
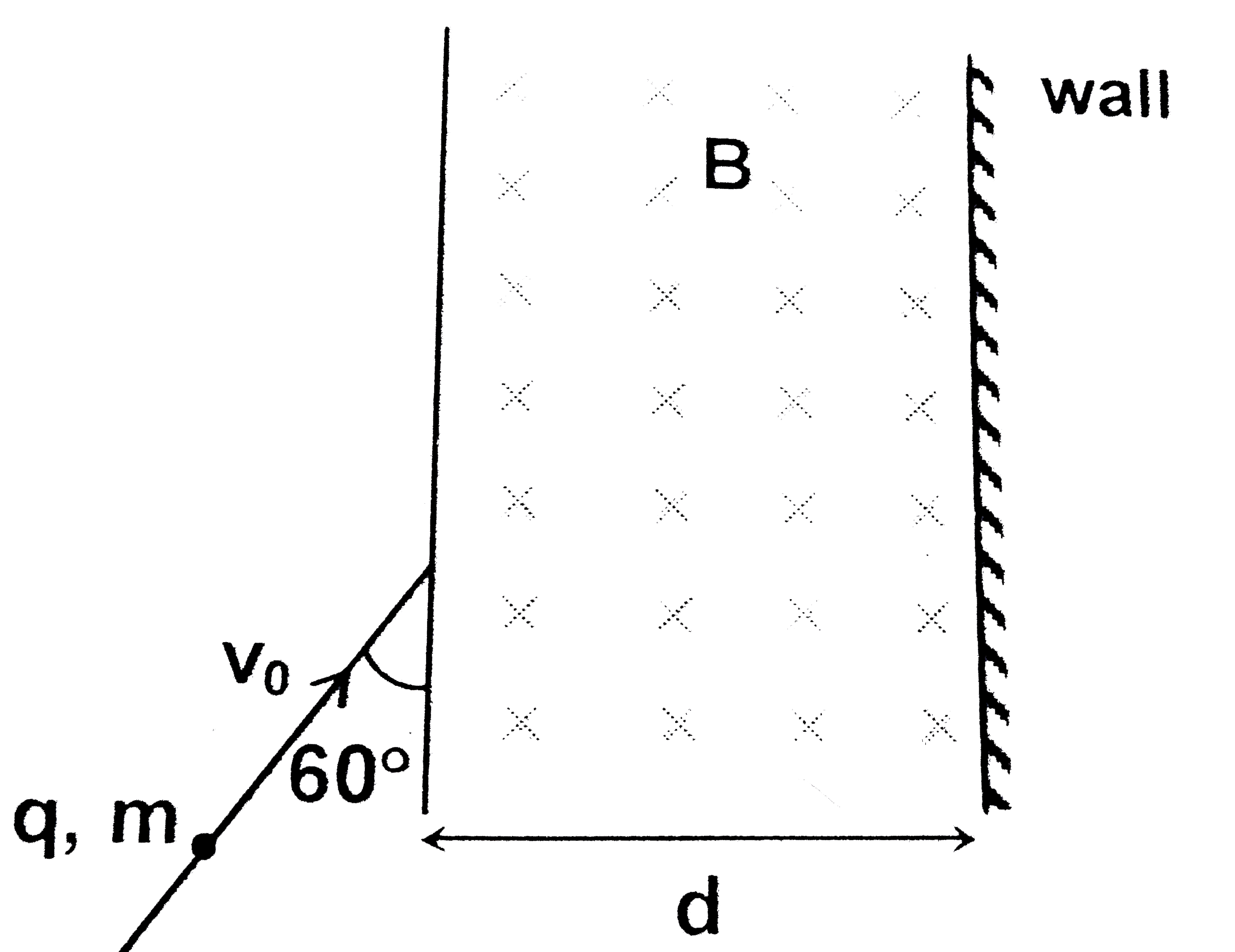
πm2qB
πm6qB
πm3qB
2πm3qB
The correct Answer is:C
Rcosθ−R/2=d=R(√3−1)2
cosθ−12=√32−12
θ=30∘
So, total angle rotates inside the magnetic field =30∘+30∘=60∘
Time period =mqbπ3=πm3qB

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find
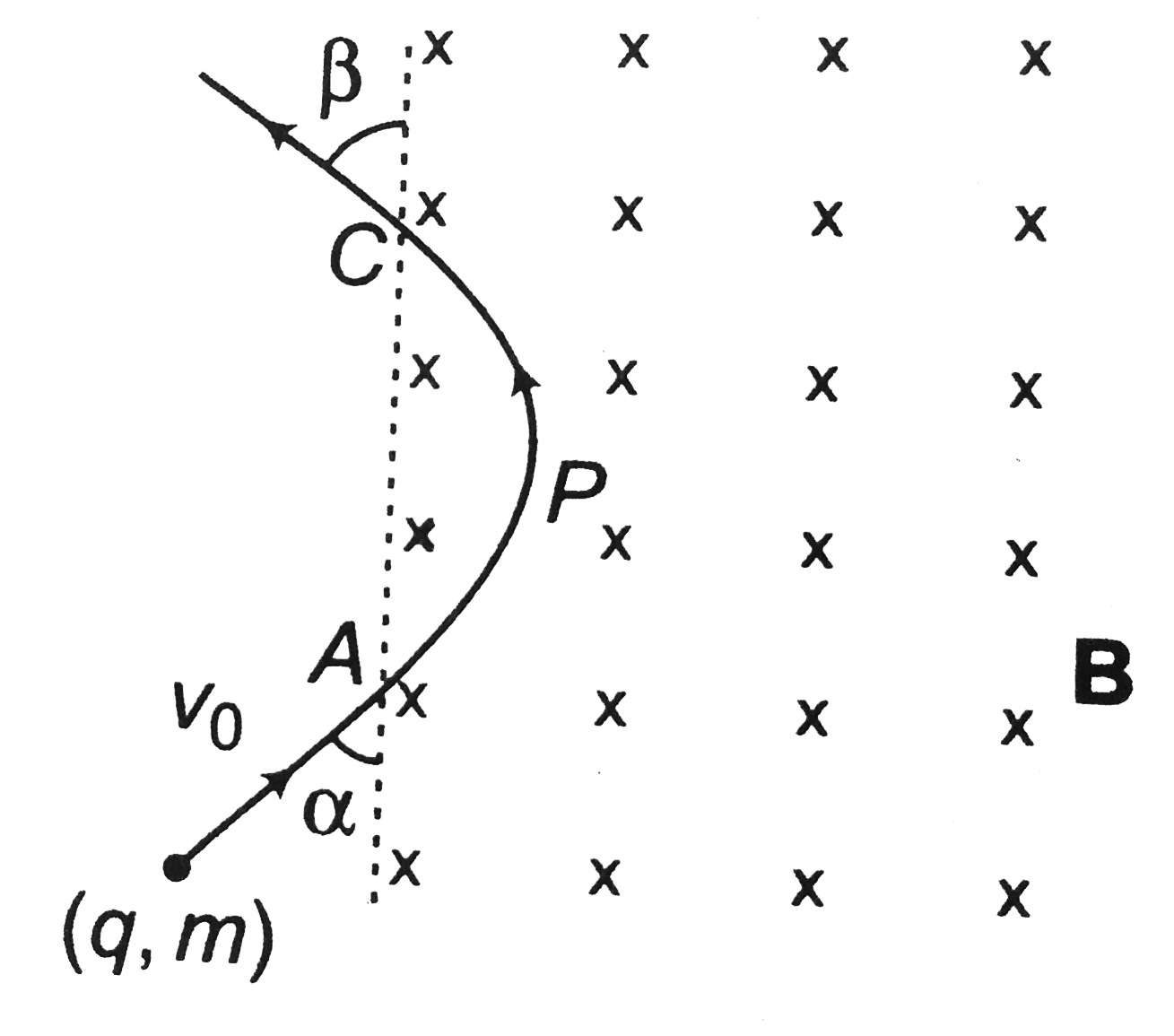
a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionA charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find

a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View Solution
Knowledge Check
A charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. The angle of deviation θ time taken by particle to cross magnetic field will be
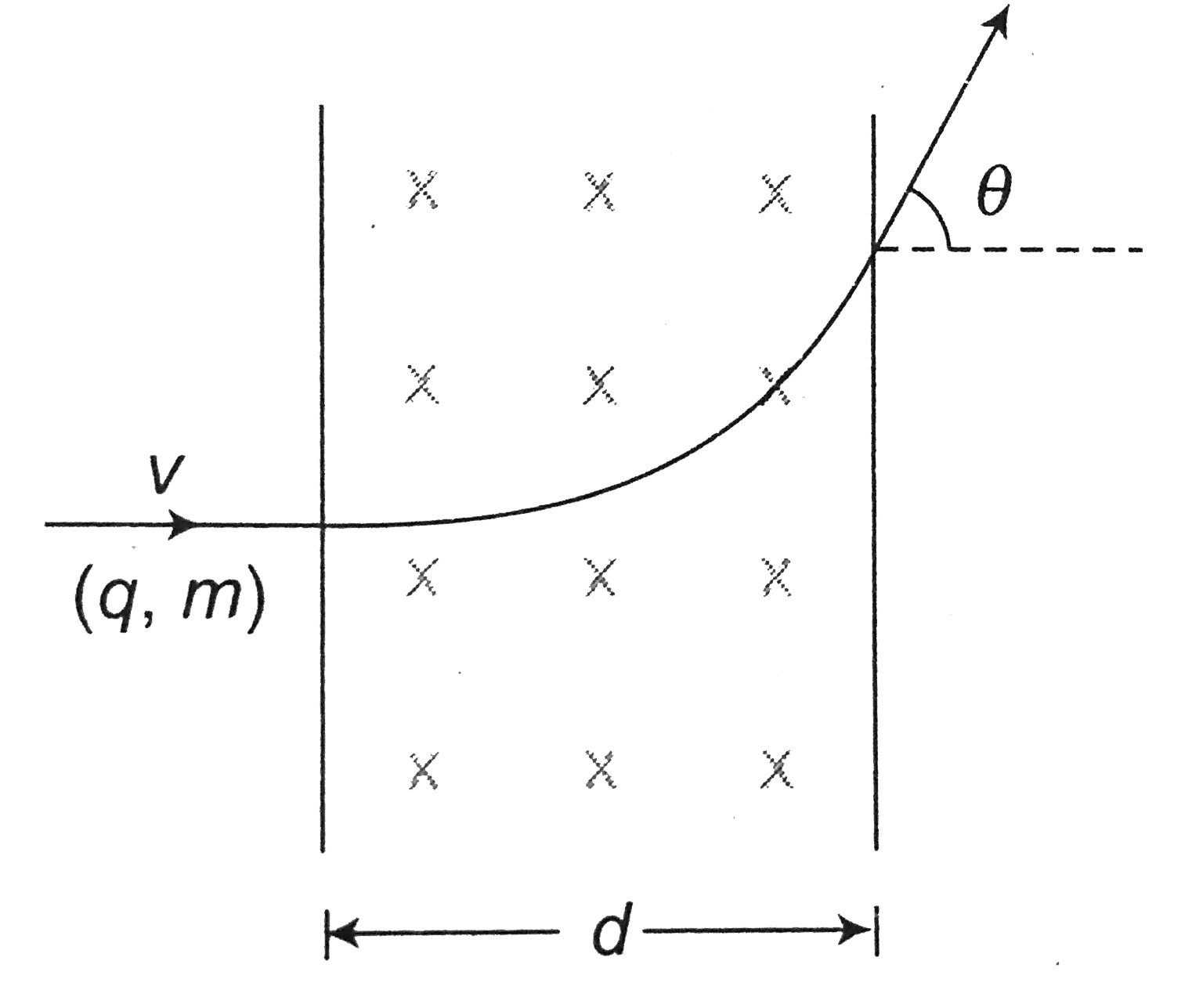 Asin−1.Bqdmv,mθBqBsin−1.Bqvmd,mθBqCcos−1.Bqdmv,mθBqDcos−1.Bqvmd,mθBq
Asin−1.Bqdmv,mθBqBsin−1.Bqvmd,mθBqCcos−1.Bqdmv,mθBqDcos−1.Bqvmd,mθBqA positively charged particle is moving with a speed v in the region of uniform magnetic induction field B as shown in figure. Which of the following statements is correct?
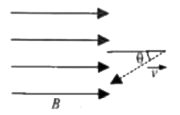 AThe force is Bqv sinθ perpendicular to B and in the plane of page.BThe force is Bqv cosθ perpendicular to the plane of the page and directed towards readerCThe force is Bqv sinθ perpendicular to the plane of the page and directed towards the reader.DThe force is Bqv sinθ perpendicular to the plane of the page and directed away from the reader
AThe force is Bqv sinθ perpendicular to B and in the plane of page.BThe force is Bqv cosθ perpendicular to the plane of the page and directed towards readerCThe force is Bqv sinθ perpendicular to the plane of the page and directed towards the reader.DThe force is Bqv sinθ perpendicular to the plane of the page and directed away from the readerA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
ADepends on the angle θBIs independent of the angle θCIs proportional to the specific charge q/m of the particleDIs inversely proportional to the value of B
A charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find

a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionA charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. Find the angle of deviation θ for particle to cross magnetic field will be

View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
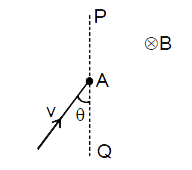
time spent
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
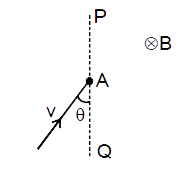
distance travelled in the magnetic field
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
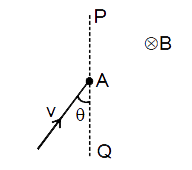
impulse of magnetic force.
View Solution
