Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
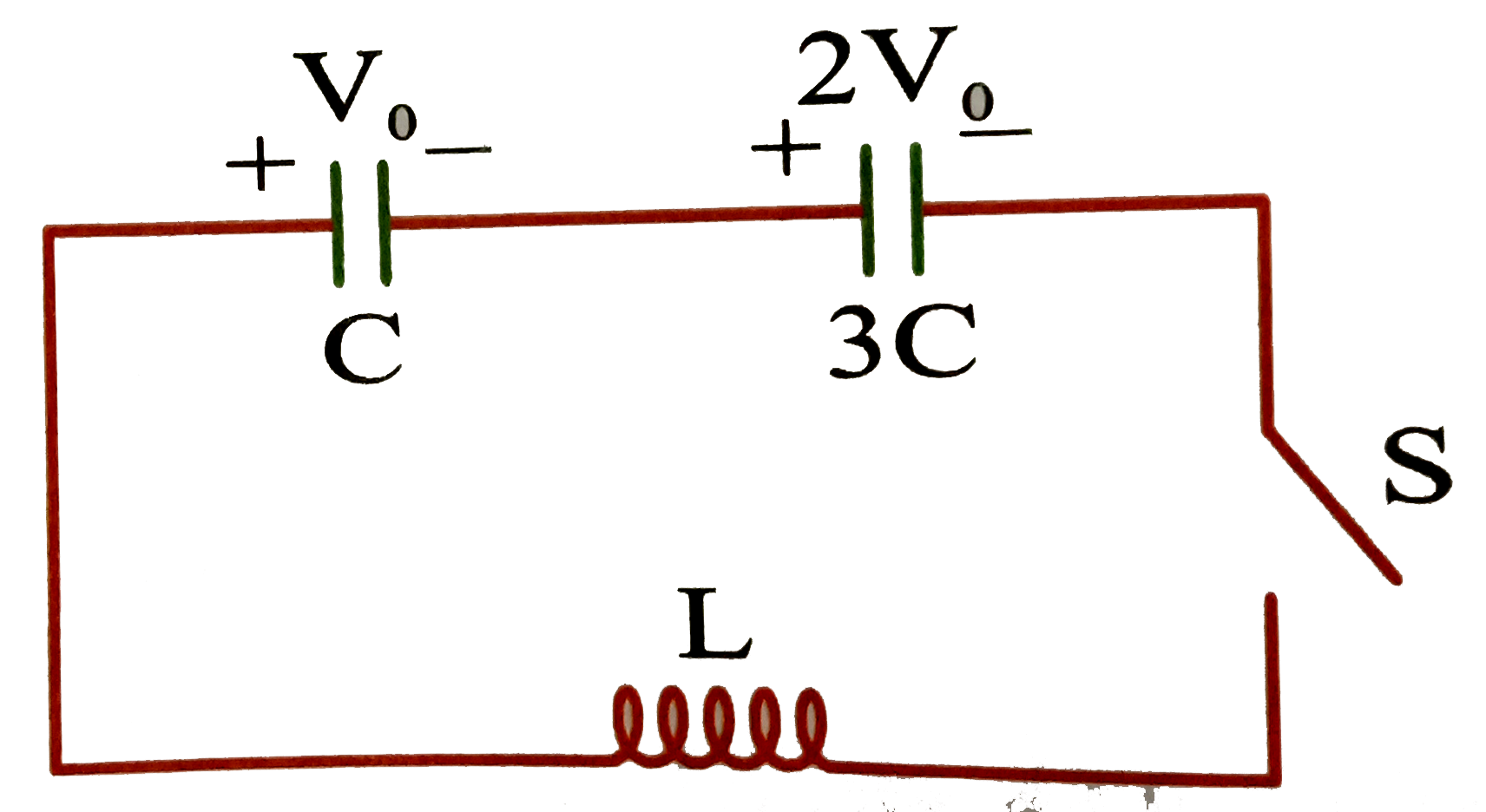
Potential difference across capacitor of capacitance 3C when the current in the cirucit is maximum is :
V04
V04
5V04
7V04
The correct Answer is:C
When current is maximum dIdt=0
e.m.f of across L=0 so potential difference across the capacitor will be same.
From the law of conservation of charge on plate 2 and 3.
3CV+CV=6CV0−CV0⇒V=54V0
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -VI
13 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Integer type questions
2 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -V
11 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
Similar Questions
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
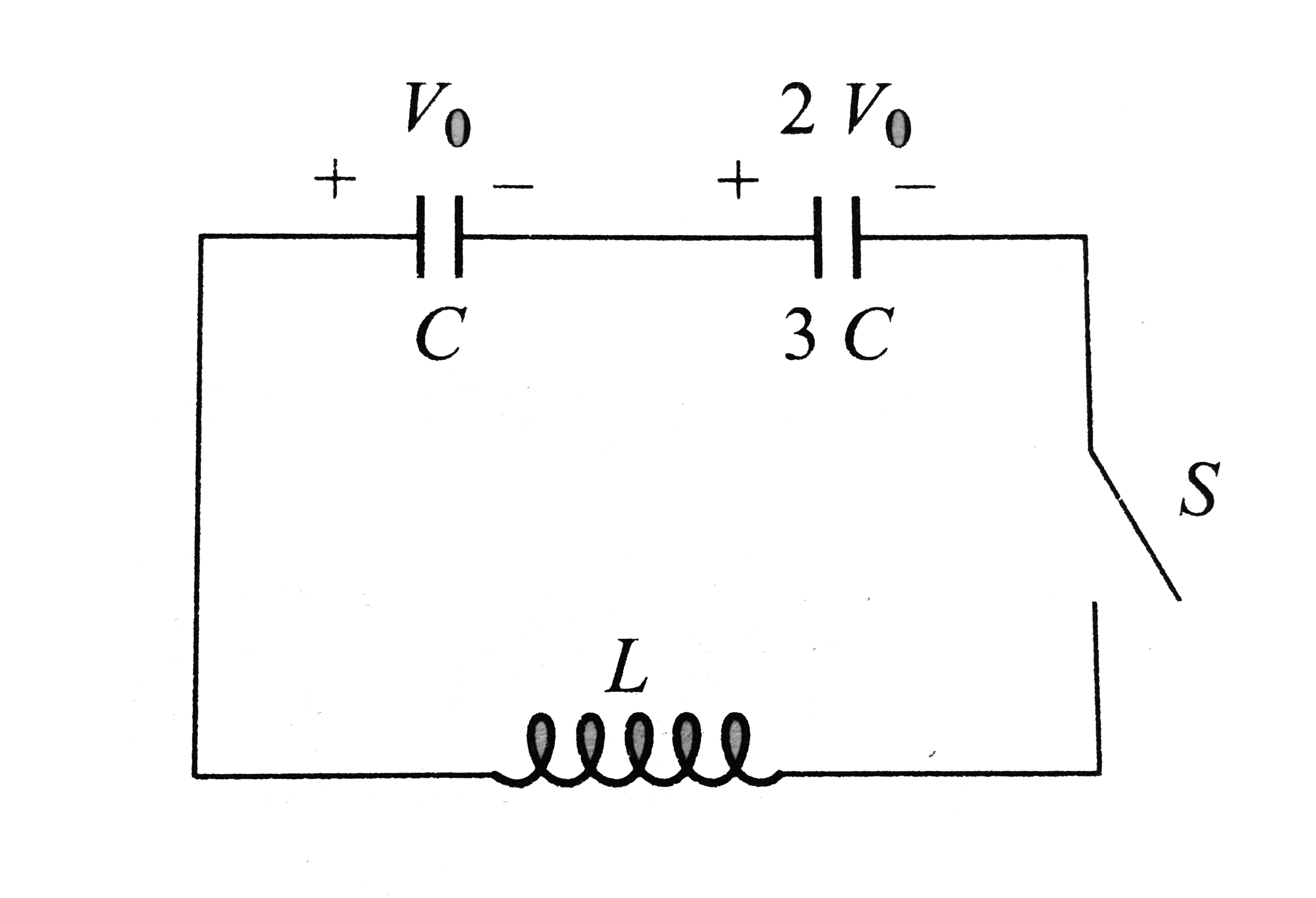
The maximum current in the inductor is
View SolutionTwo capacitors 2C and 4C initially charged to potential difference of V0and3V0 with the potential as show are connected to an inductor of inductance L. Initial curren tin the inductor is zer. Now the swtich 'S' is closed. The maxmimum current in the circuit is
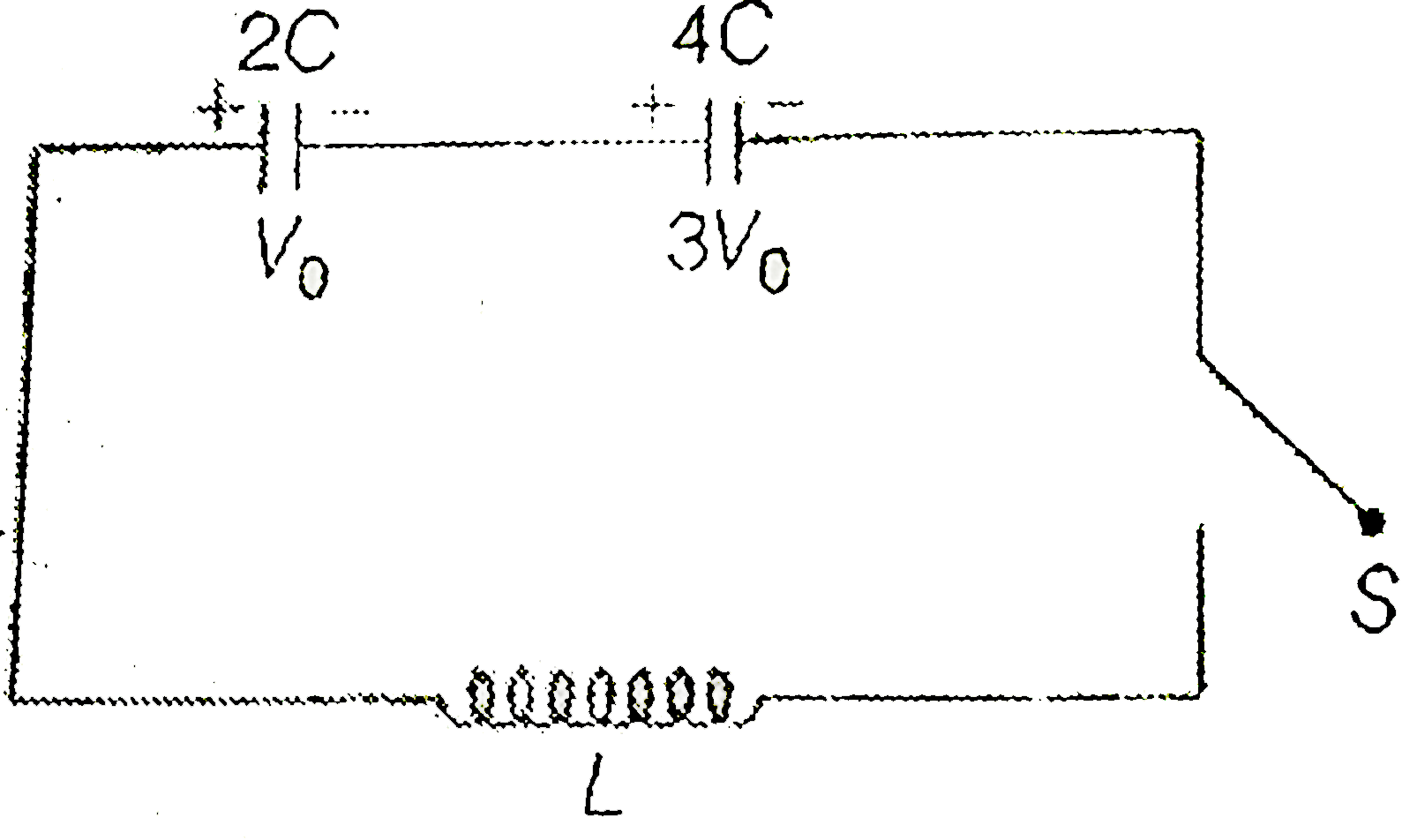
View Solution
Knowledge Check
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum isAV04BV04C5V04DNone of theseTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum isAV04B3V04C5V04DNone of theseTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.

The maximum current in the indcutor is :A3V02√3CLBV0√3CLC2V0√3CLDV0√CL
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then

View SolutionA capacitor having capacitance 2 μF is charged to a potential difference of 50 V. it is then diconnected from battery and connected to an inductor of inductance 5 mH. Peak current that flows through the inductor is
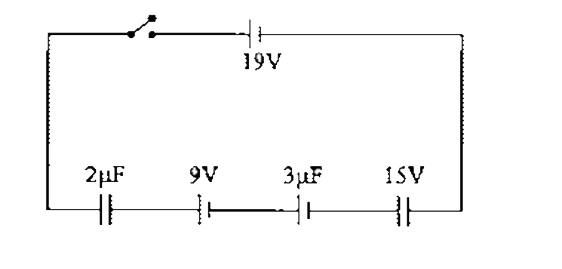
View SolutionThe two capacitors in the circuit shown in figure are initially uncharged and then connected as shown and switch is closed. What is the potential difference across 3μF capacitor?
View SolutionA capacitor of capacitance 4μF is fully charged to a potential difference of 12 V and then charging battery is disconnected. Charged capacitor is now connected across an inductor of self-inductance of 1.2 mH. The current in the circuit at a time when the potential difference across the capacitor is 6 V is
View SolutionA capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 0.2mH. At an instant when potential difference across the capacitor is 6v
View Solution