A block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction $μ$ and compresses a spring with force constant $k$ a distance $x$ before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

A

$m g h' = m g h - μ m g d$

B

$m g h' = m g h + μ m g d$

C

$m g h' = m g h + μ m g d + k x^{2}$

D

$m g h' = m g h - μ m g d - k x^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Final $P . E .$ of block $=$ Initial $P . E .$ of block $+$ work done by friction
$∴ M g h' = m g h - μ m g d$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block of mass m slides from rest at a height H on a frictionless inclined plane as shown in the figure. It travels a distance d across a rough horizontal surface with coefficient of kinetic friction $μ$ , and compresses a spring of spring k by a distance x before coming to rest momentarily. Then the spring extends and the block travels back attaining a final height of h. Then

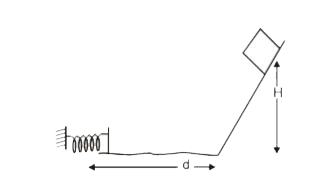A $h = H - 2 μ (d + x)$
B $h = H + 2 μ (d + x)$
C $h = H - 2 μ d + k x^{2} / m g$
D $h = H - 2 μ (d + x) + k x^{2} / 2 m g$
Question 2 - Select One
A block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
A $sin θ$
B $cos θ$
C $cot θ$
D $tan θ$
Question 3 - Select One
A block has been placed on an inclined plane . The slope angle of $θ$ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
Asin $θ$
Bcos $θ$
Cg
Dtan $θ$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 42

Home
Ask Doubt
Profile