A particle is attached with a string of length $l$ which is fixed at point $O$ on an inclined plane what minimum velocity should be given to the particle along the incline so that it may complete a circle on inclined plane $($ plane is smooth and initially particle was resting on the inclined plane . $)$

A

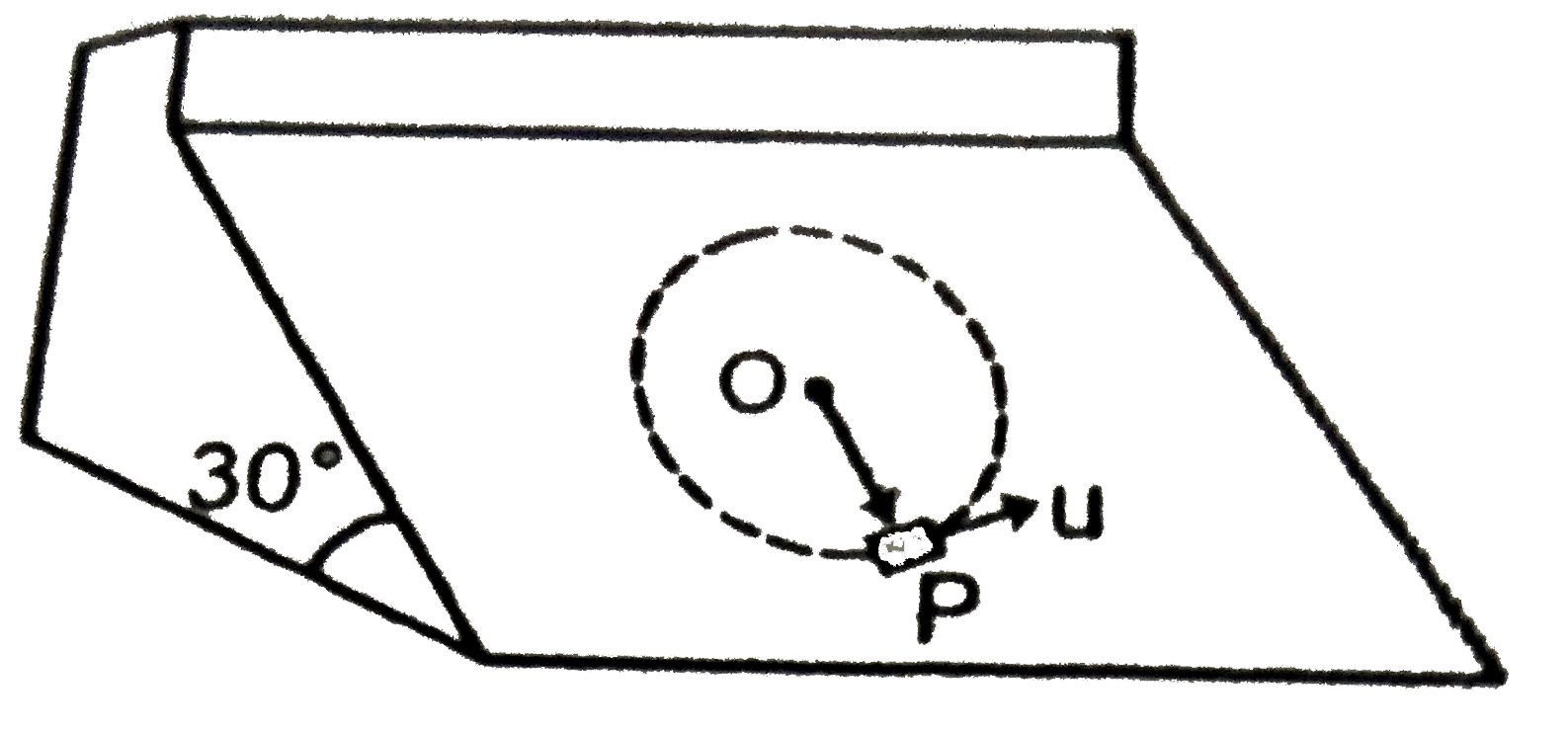
$\sqrt{5 g l}$

B

$\sqrt{\frac{5 g l}{2}}$

C

$\sqrt{\frac{5 \sqrt{3 g l}}{2}}$

D

$\sqrt{4 g l}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The side view of circular motion is as shown $:$

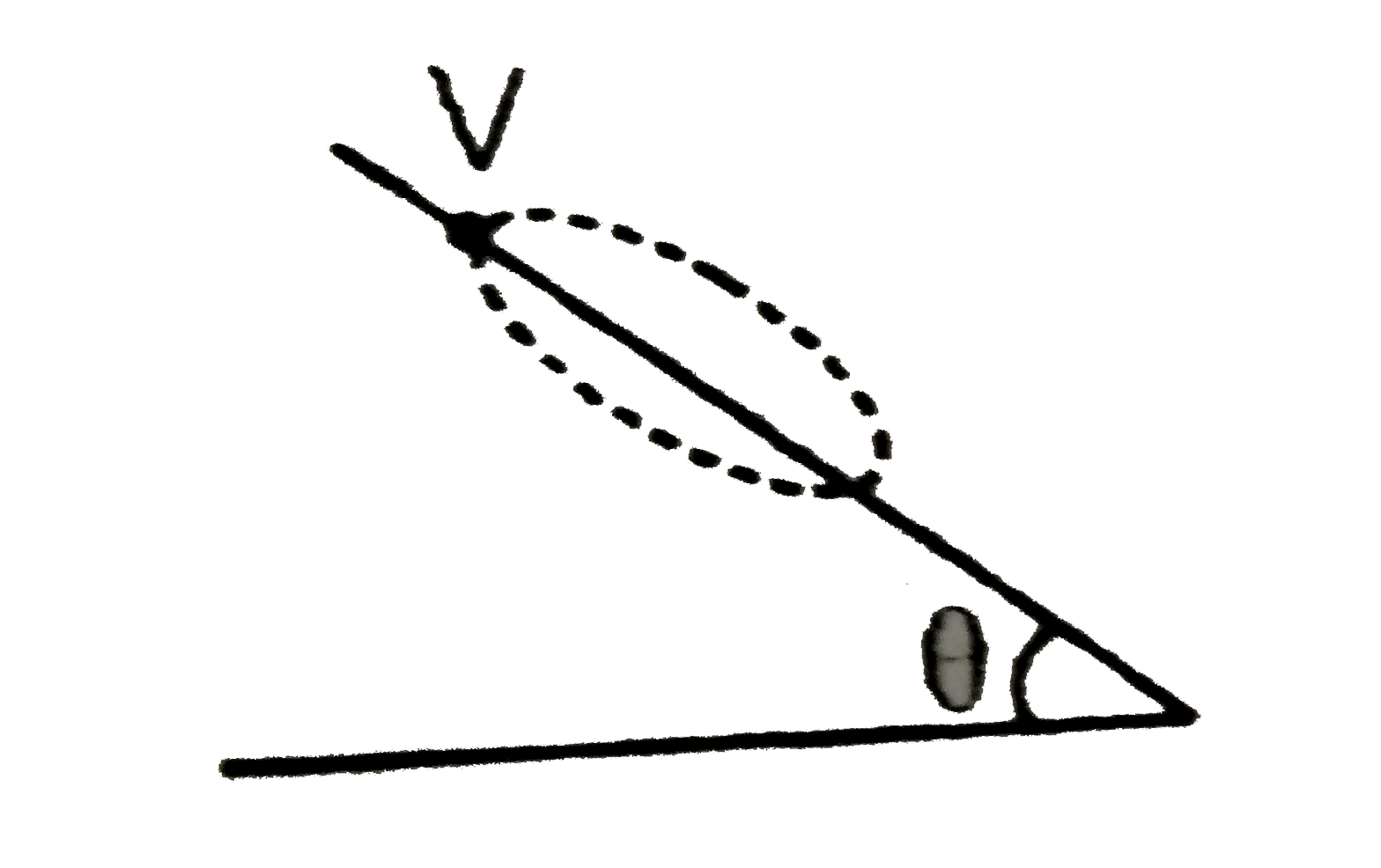
$T + m g sin θ = \frac{m v^{2}}{R}$
and by energy conservation $:$
$\frac{1}{2} m v_{i}^{2} = \frac{1}{2} m v^{2} + m g 2 R (sin θ)$
for $v_{i}$ to be minimum, $v$ is minimum and hence $T = 0$
$\Rightarrow v_{i}^{2} = 5 g R, sin θ$
$\Rightarrow v_{i})_{min} = \sqrt{\frac{5 g l}{2}} A n s .$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The ratio of the range of the particle and its maximum range in the inclined plane is:
A $1 : 2$
B $1 : \sqrt{2}$
C $1 : \sqrt{3}$
D $1 : 1$
Question 2 - Select One
A particle is projected on an inclined plane with a speed $u$ as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
.
A $\frac{2 u^{2} \sqrt{3 + 1}}{3 g}$ .
B $\frac{4 u^{2} \sqrt{3 - 1}}{9 g}$ .
C $\frac{2 u^{2} \sqrt{5 - 1}}{8 g}$ .
D $\frac{2 u^{2} \sqrt{3 - 1}}{3 g}$
Question 3 - Select One
A particle of mass $m$ attached to a string of length $l$ is descending circular motion on a smooth plane inclined at an angle $α$ with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
A $\sqrt{5 g l}$
B $\sqrt{5 g l (cos α + 1)}$
C $\sqrt{5 g l / tan α}$
D $\sqrt{5 g l sin α}$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 51

Home
Ask Doubt
Profile