The string is now replaced by a spring of spring constant k and natural length l. Mass 2m is fixed at the bottom of the frame . The mass m which has the other end of the spring attached to it is brought near the mass 2m and released as shown in figure. The maximum angle θ that the spring will substend at the centre will be :( Take k=10N/m,l=1m,m=1kg and l=r)

60∘
30∘
90∘
None of these
The correct Answer is:A
Length of spring at maximum =2lcosϕ
∴ Extension is x=(2lcosϕ−l)
Now initial potential energy of the spring is converted into final PE of spring and gravitational PE.
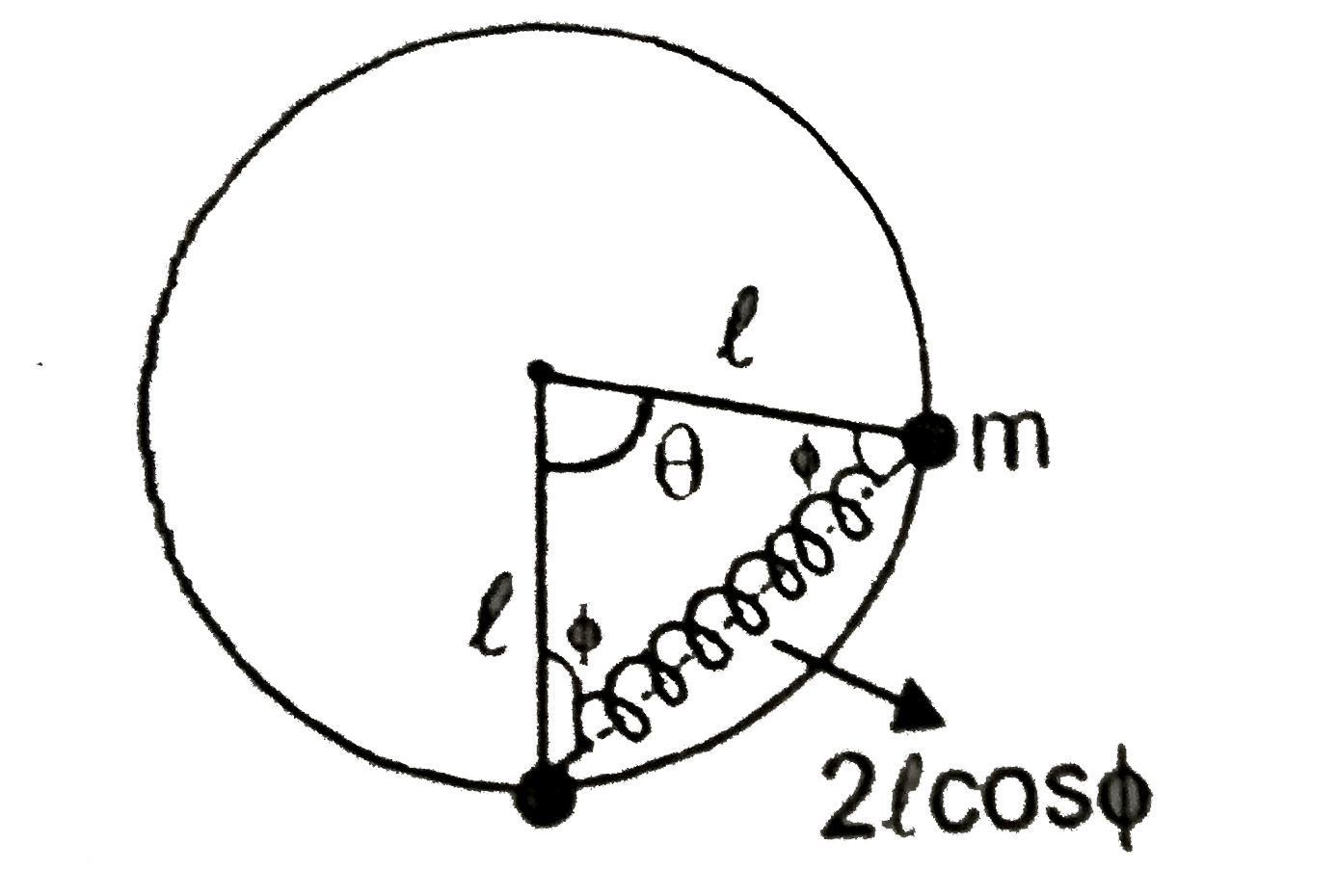
∴12kl2=12k(2lcosθ−l)2+mg(l−lcosθ)
Putting values
12×10×12=12×10(2cosϕ−1)2+10(1−cosθ)
∵θ=π−2ϕ
5=5(2cosϕ−1)2+10(1+cos2ϕ)
1=(4cos2ϕ+1)1−4cosϕ)+2(1+2cos2ϕ−1)
8cos2ϕ=4cosϕ
∴cosϕ=12
∴ϕ=60∘
θ=60∘.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 51
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 52
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 49
Explore 6 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
In the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
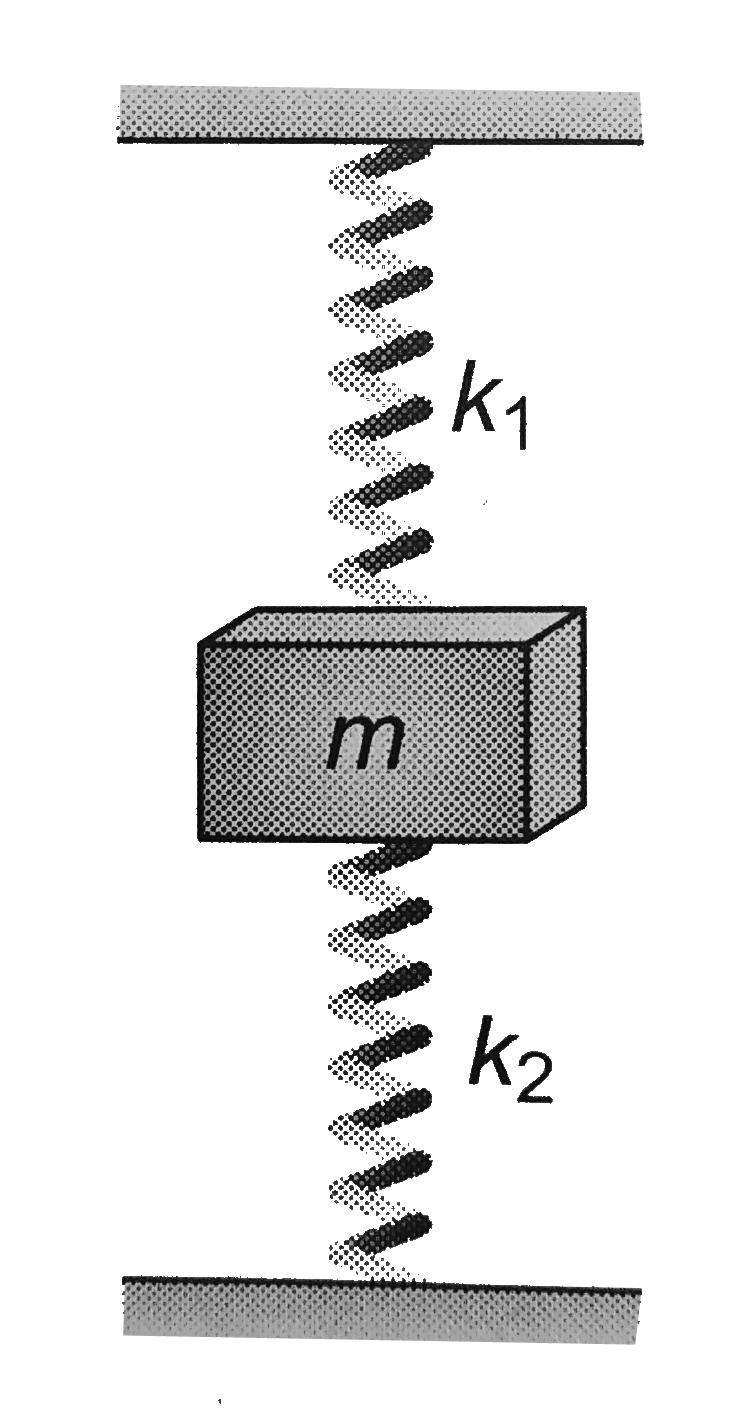 Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.
Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.An ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
A4MgKB2MgKCMgKDMg4KAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2k
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA bob of mass m is connected to a spring of spring constant k and a string which is fixed to the ceiling as shown in figure. Original length of the spring is L and the bob rotates in a horizontal circle centred at the fixed rod. Assuming the spring remains horizontal, then elongation in the spring is :

View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View Solution
