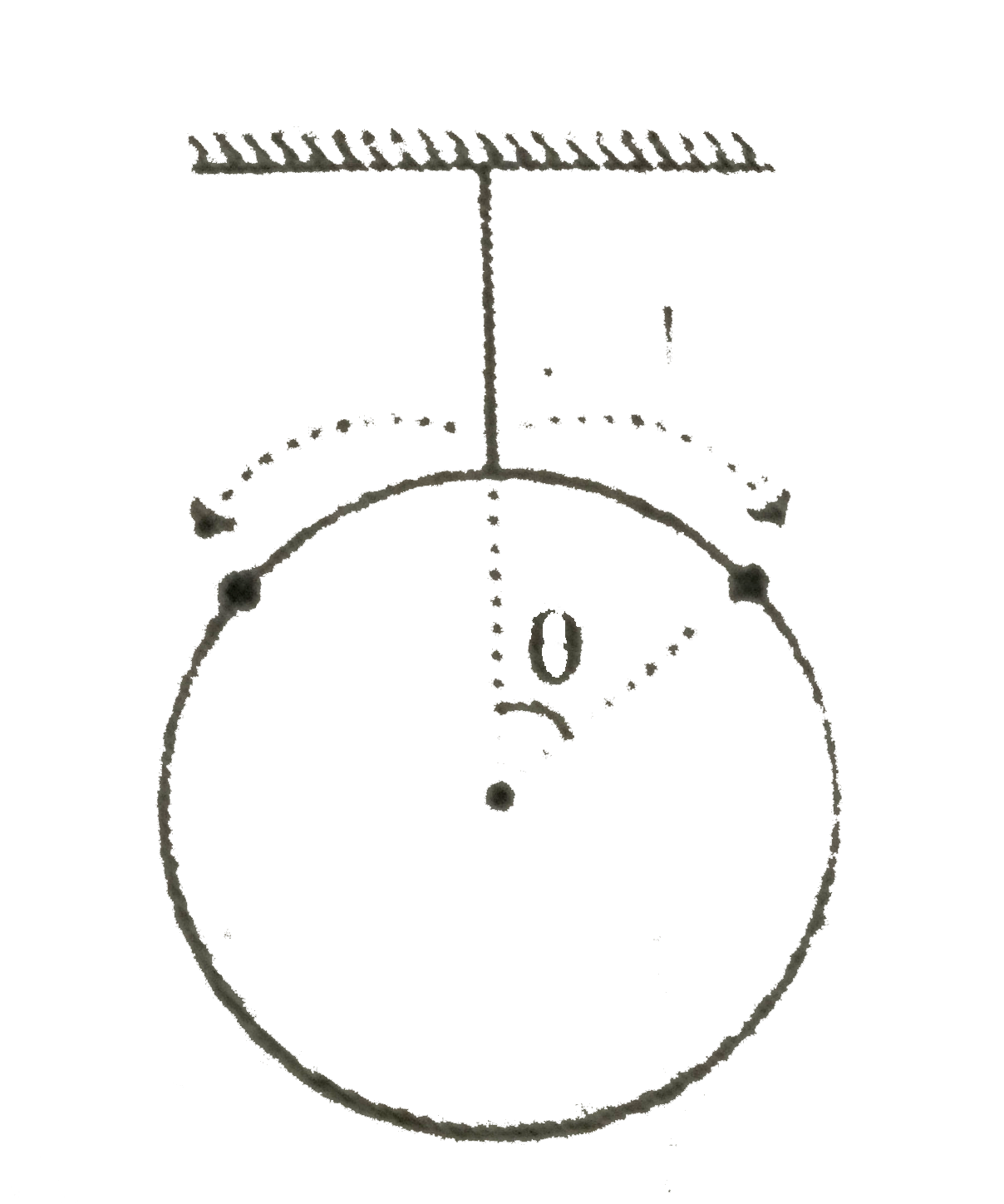
A massless ring hangs from a thread and two beads of mass m slide it without friction. The beads are released simultaneously from the top of the ring and slide down along possible sides. Find the angle from vertical at which the ring will start to rise.
The correct Answer is:A, B, C
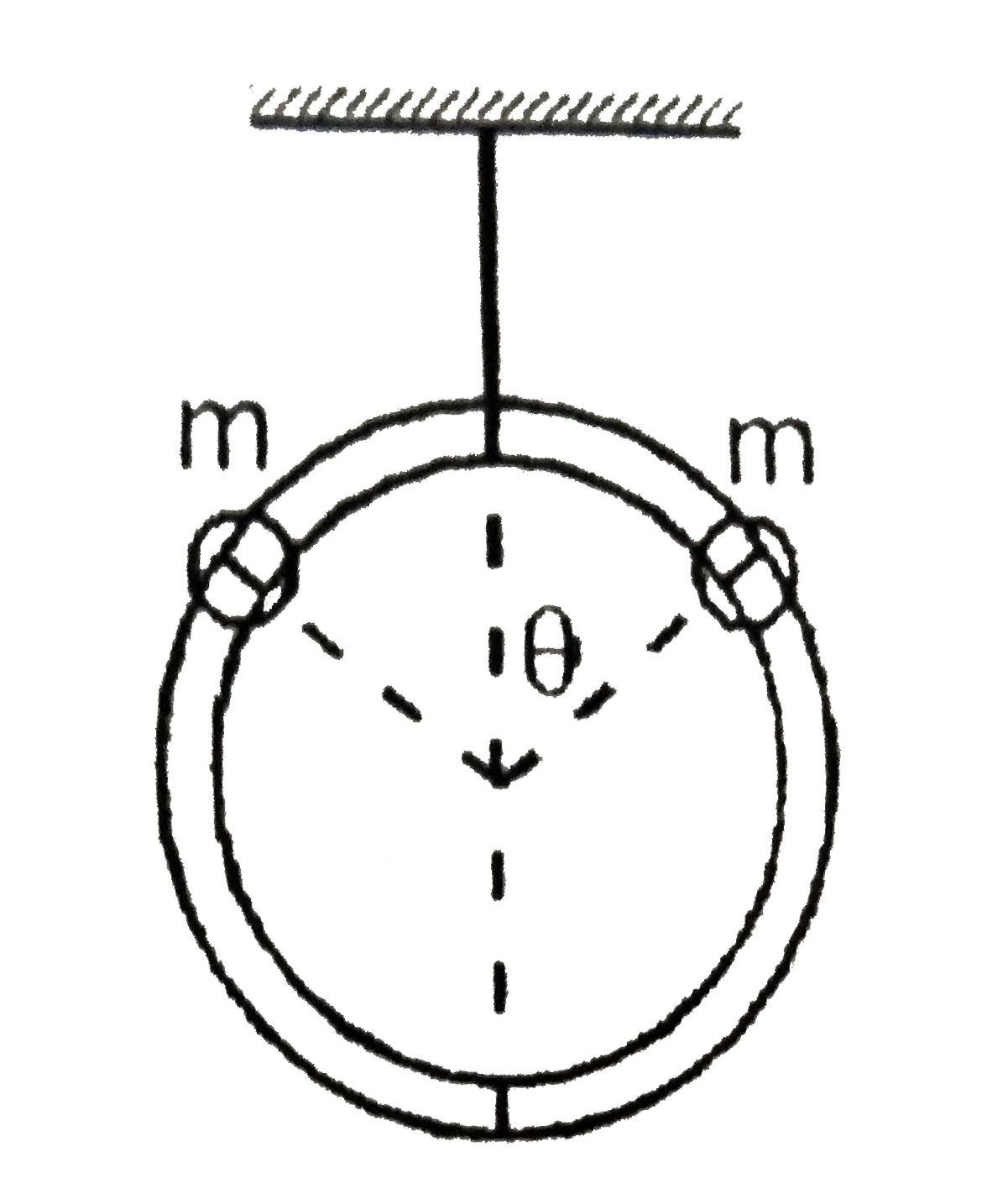
at α=cos−1(23) balls will leave contact with inner wall and came in contact with outer wall then force on ring will be 2Ncosα in upward direction.
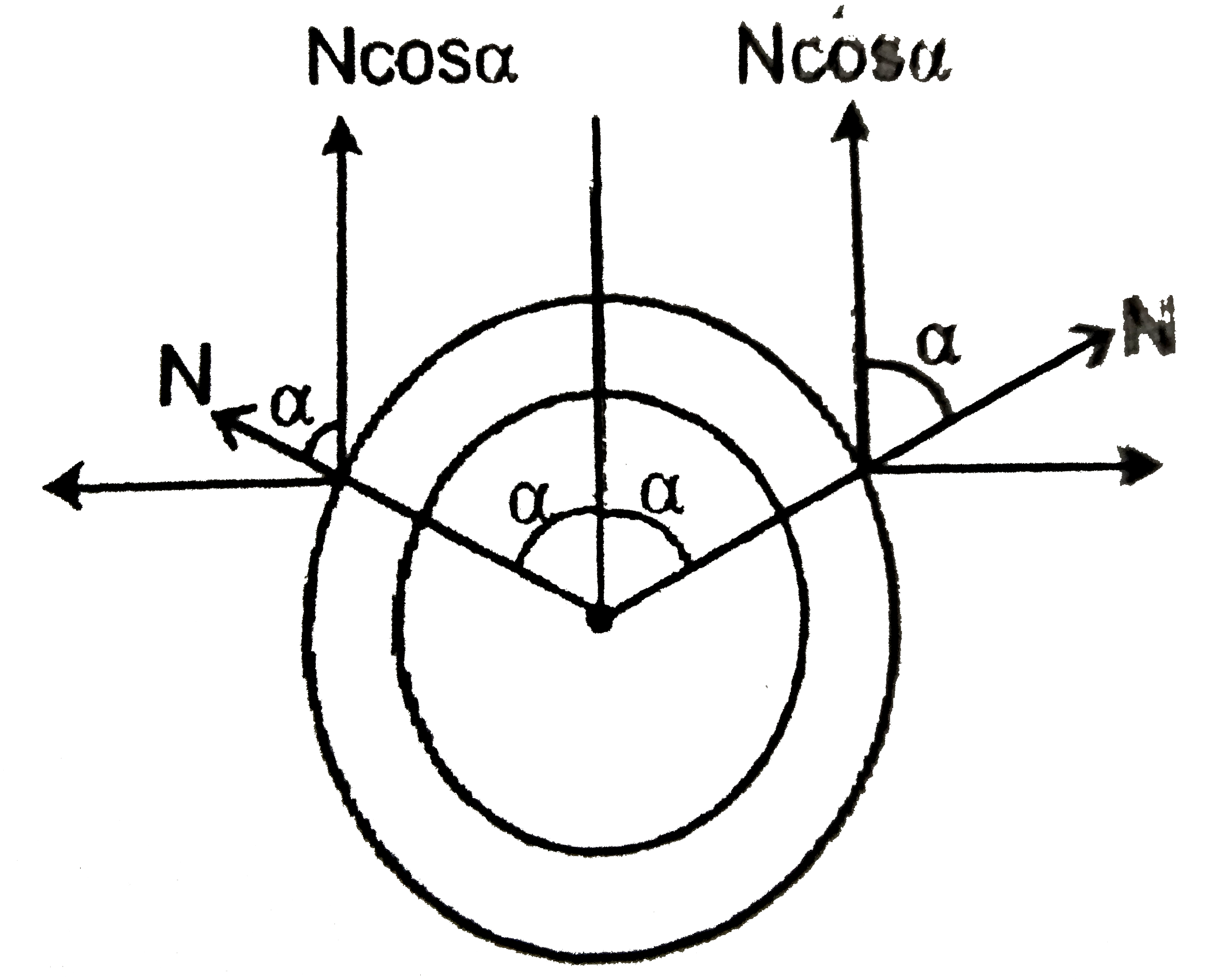
So ring will start rising as it is massless .
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 595videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 605videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 577videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A ring of mass M hangs from a thread and two beads of mass m slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if m>3M2 . ltbr>
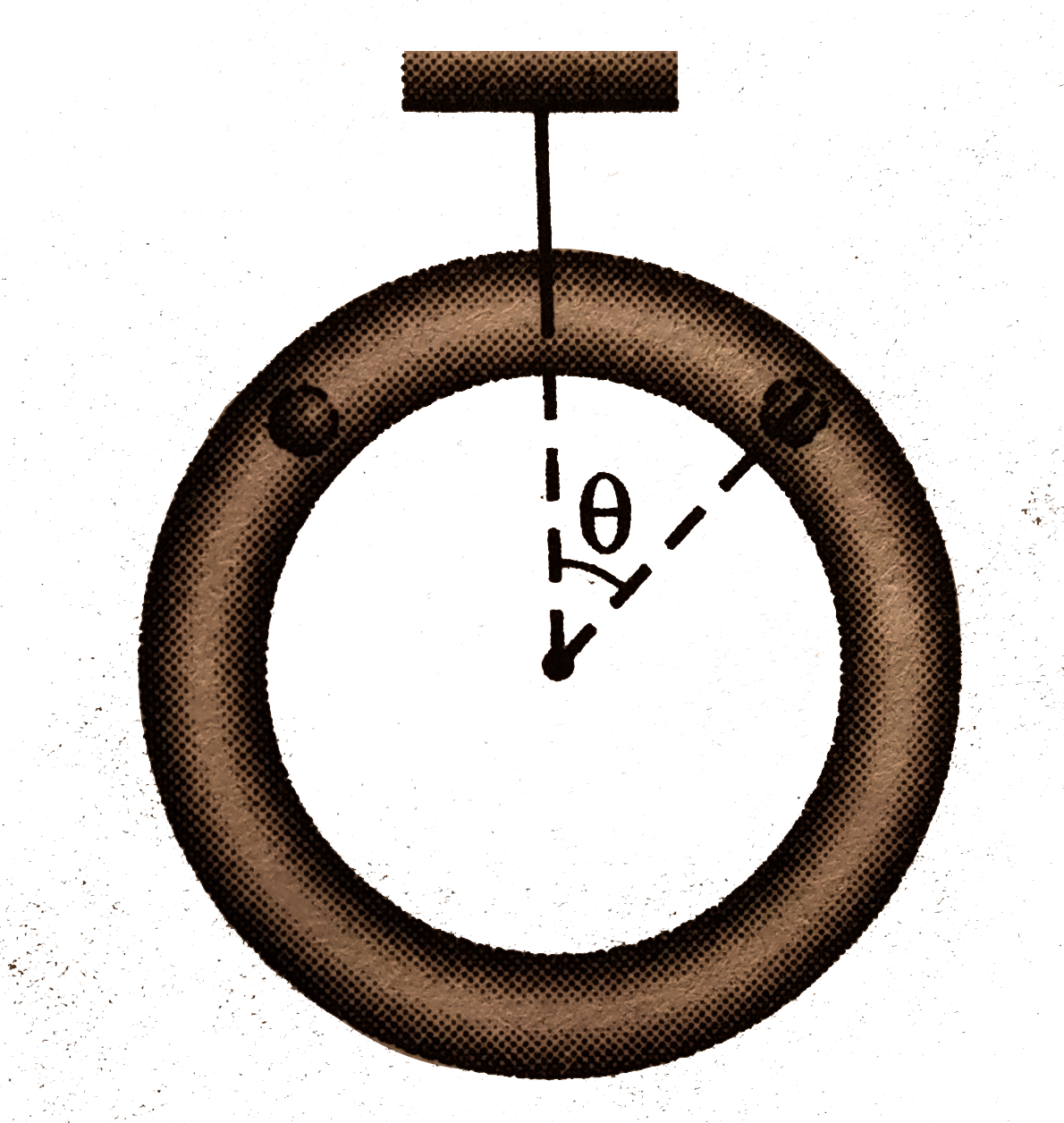View SolutionA tube of mass M hangs from a thread and two balls of mass m slide inside it without friction (see figure). The balls are released simultaneously from the top of the ring and slide down on opposite sides. θ defines the positions of balls at any time as shown in figure
(a) Show that ring will start to rise if m≥3M2.
(b) If M=0 , find the angle θ at which the tube begins to rise.View Solution
Knowledge Check
- Question 1 - Select One
Two beads are released from A simultaneoulsy to slide along smooth AB and AC. Find the ratio of time taken by them to reach B and C respectively
A2:1B3:1C1:1D4:1 - Question 2 - Select One
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :
Ag2B(√3g)(2)Cg√2Dg - Question 3 - Select One
A head slide without friction around a loop the (figure). The bead slide is released is from rest at a height h=3.50R. How large is the normal force on the bead at point (A) if its mass is 50g ?
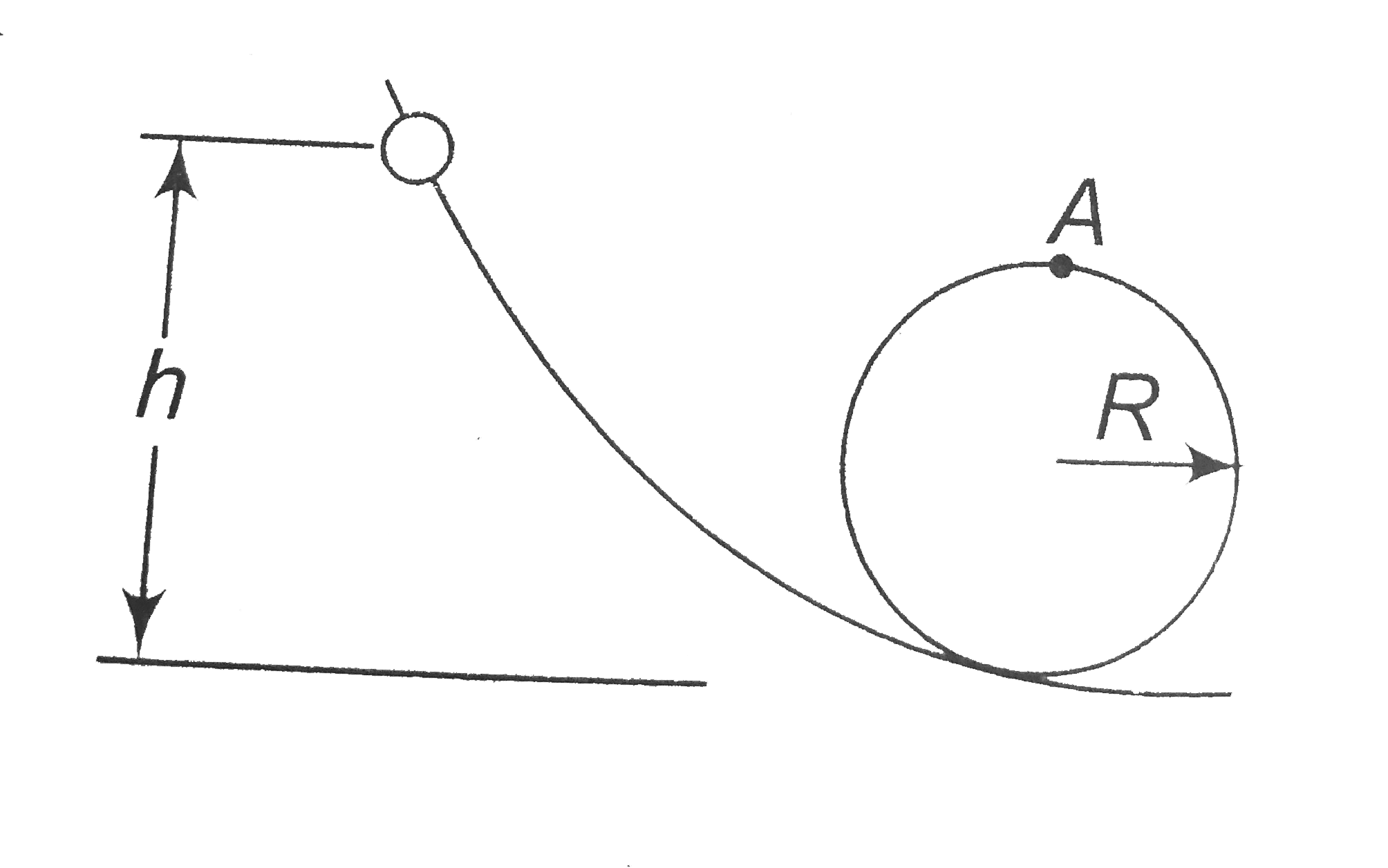A0.10N downwardB0.10N upwardC1.0N downwardD1.0N upward
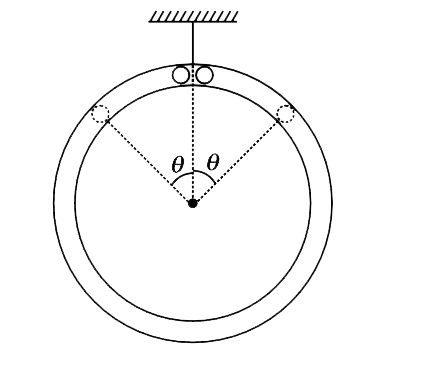
Fig. 3E.47 (a) shows a circular ring of mass M that hangs in a vertical plane. Two beads of mass m are released simultaneously from the top of the ring in opposite directions. There is no frictional force between the bead and the ring. Show that the ring will starts to rise if m>3M2. If m = 2M, at what angle θ from vertical this happends ?
(a)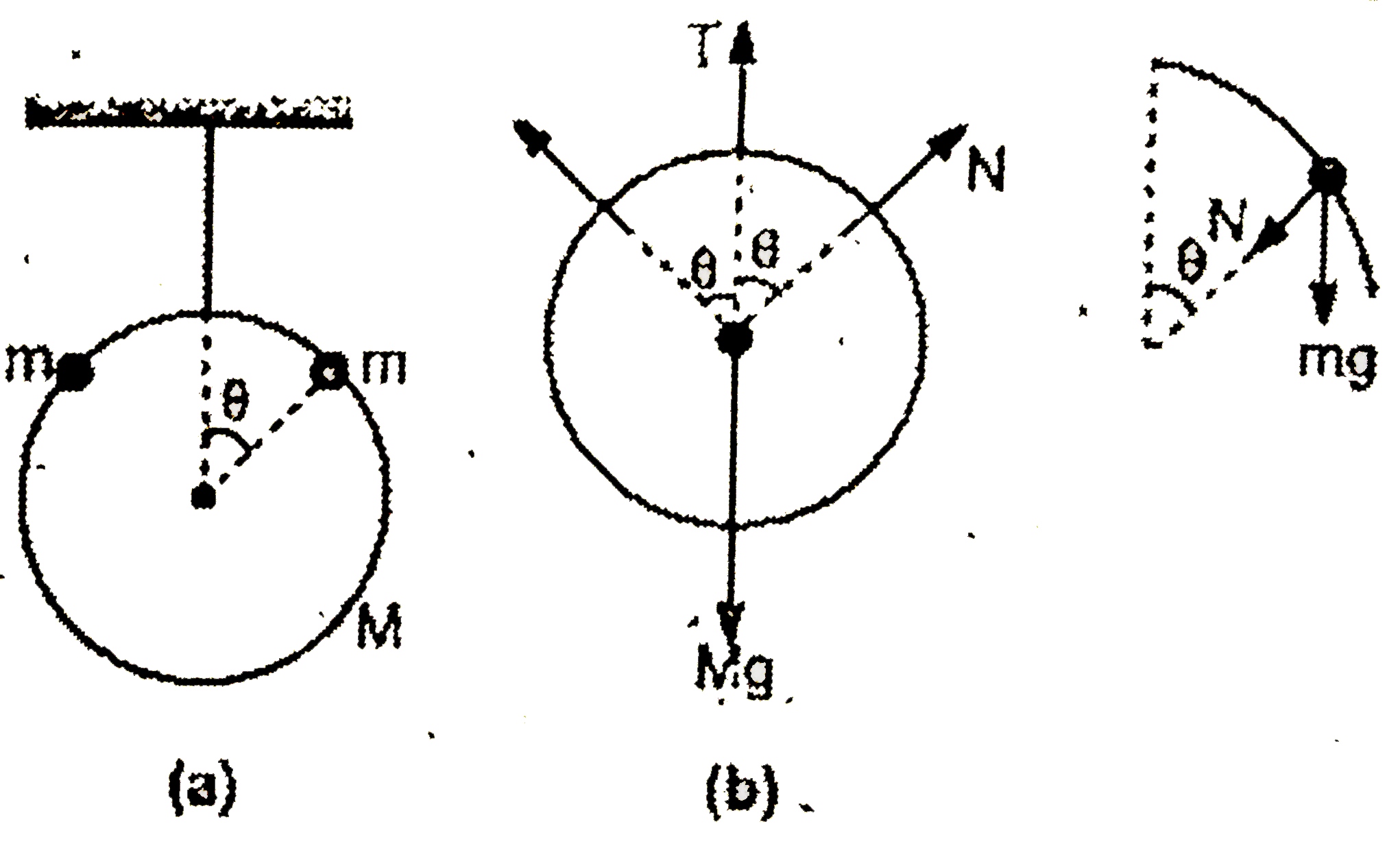
View SolutionA and B are two identical rings released from the top of an inclined plane . A slides down and B rolls down. Then which reaches the bottom first ?
View Solution
The figure shows a thin ring of mass M=1kg and radius R=0.4m spinning about a vertical diameter (take I=12MR2) A small beam of mass m=0.2kg can slide without friction along the ring When the bead is at the top of the ring the angular velocity is 5rad/s What is the angular velocity when the bead slips halfwat to θ=45∘?View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
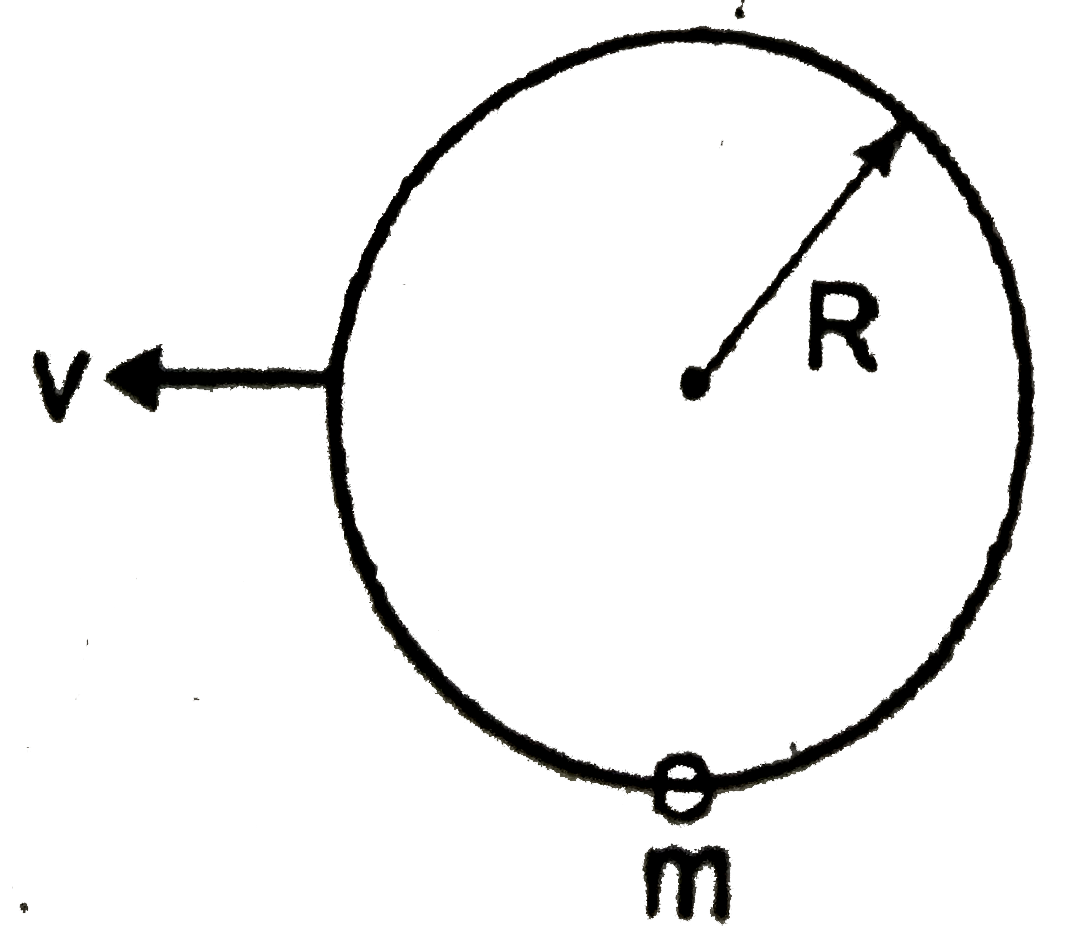View SolutionA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
View Solution