A spherical cavity is formed a solid sphere by removing mass from it. The resultant configuration is shown in figure. Find out the moment of inertia this configuration about the axis through centre of the solid sphere as shown . Take mass M( uniform ) for the configuration and radius R for solid sphere and radius R/2 for cavity.
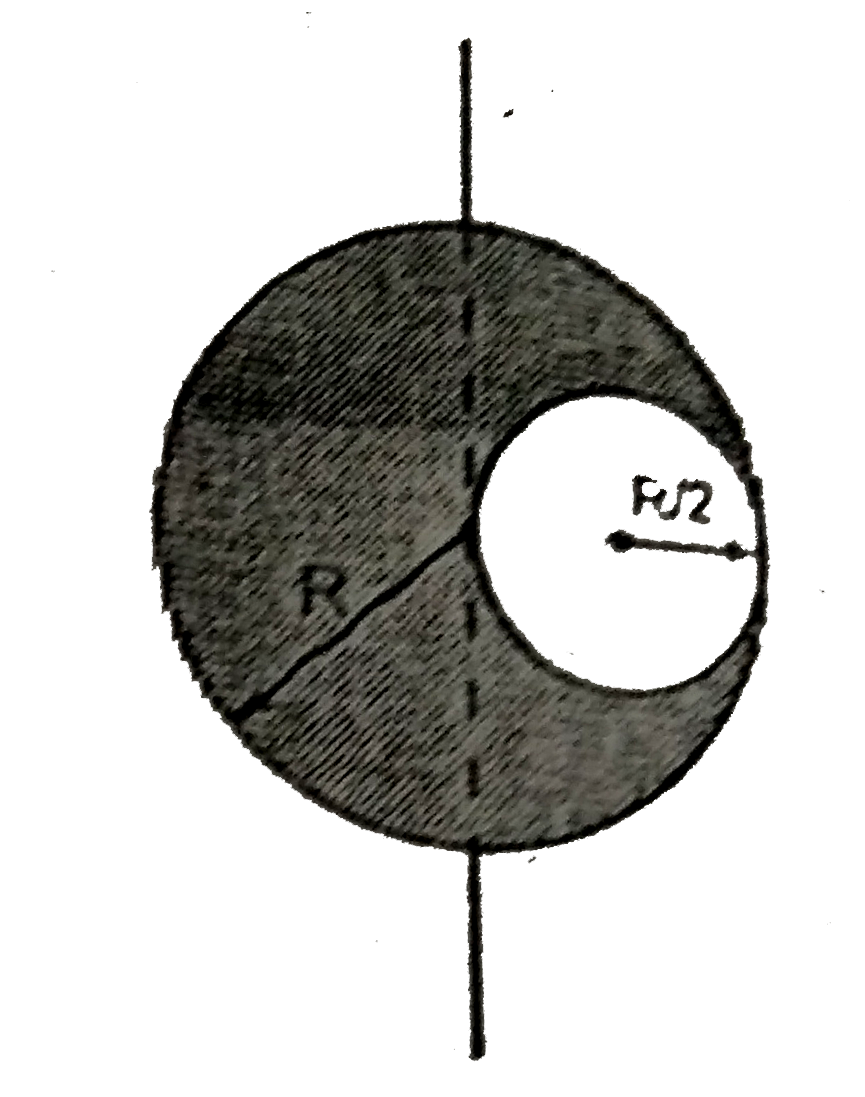
The correct Answer is:I=57140MR2

ρ=M(4/3)πR3−(4/3)π(R/2)3
I=25MR2−(25M2(R2)2+M2(R2)2)
,I=57140MR2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 59
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 60
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 57
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Knowledge Check
A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 Axcm=−R/15Bycm=−R40Czcm=zeroDNone of these
Axcm=−R/15Bycm=−R40Czcm=zeroDNone of theseThe moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
A25MR2B63MR2C45MR2D75MR2A solid sphere and a hollow sphere are identical in mass and radius. The ratio of their moment of inertia about diameter is :
A5:3B1:1C1:2D3:5
The moment of inertia of a sphere about its diameter is I. Four such spheres are arranged as shown in figure. Find the moment of inertia of the system about the axis XX'. (radius of each sphere is 2R).

View Solution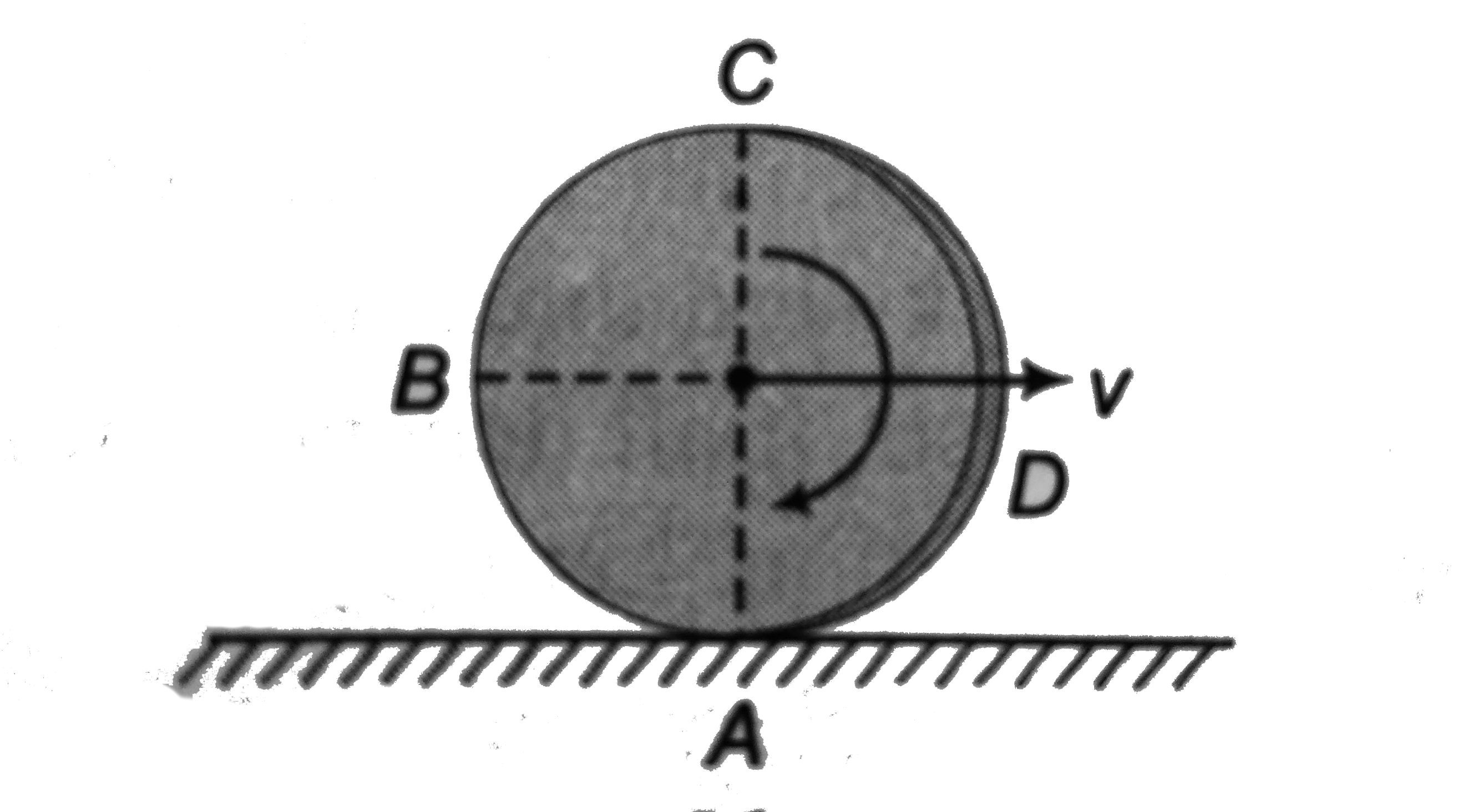
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

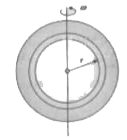
View SolutionFind the moment of inertia of solid sphere of mass M about a diameter as shown in Fig.
View SolutionThee spheres each of mass M and radius R are placed in contact with each other as shown in the figure here. Then the moment of inertia of the system about the axis CC' is

View Solution
