Two beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )
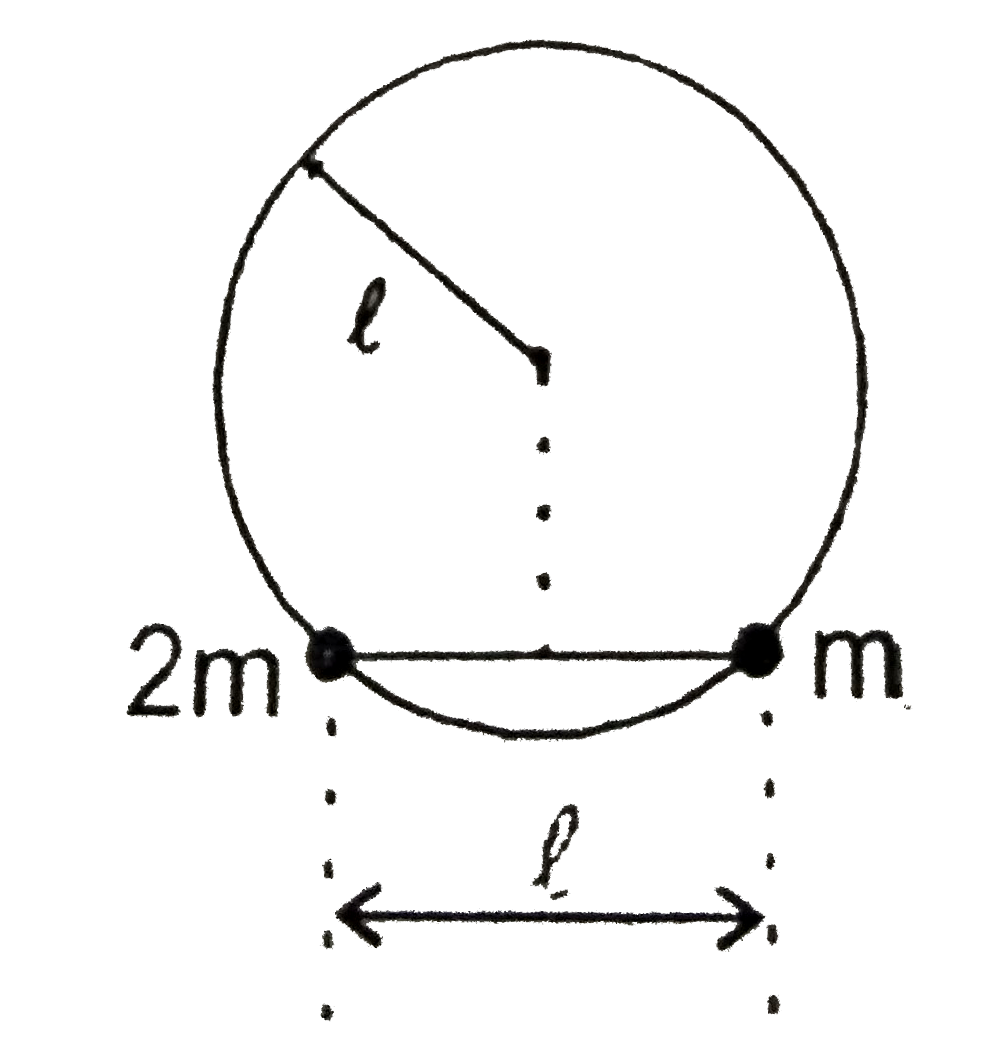
If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :
Mass 2m will arrive earlier at the bottom
Mass m will arrive earlier at the bottom.
Both the masses will arrive together but different speeds.
Both the masses will arrive together with same speeds.
The correct Answer is:D
The speeds given to 2m will also be possessed by m
∴KE in horizontal position gets converted in PE in vertical position.
122mv2+12mv2= change in PE in vertical position.

ΔPE=2mg[lcos30∘−lcos60∘]+mg[lcos30∘+l2]
2mg[l√32−l2]+mg[l√32+l2]
∴mgl[√3−1]−mgl[√3+12]
=mgl[√3−1+√32+12]=mgl[3√32−12]
K.E.=123mv2=mgl[3√3−12]
∴v=√3√3−13gl Ans.
Both the masses will have same magnitude of acceleration all the time.
∴ Their velocities and distance covered will same.
Hence (D).
Similar Questions
Two particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

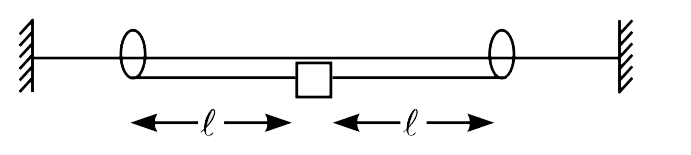
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
View Solution
Knowledge Check
Two beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )
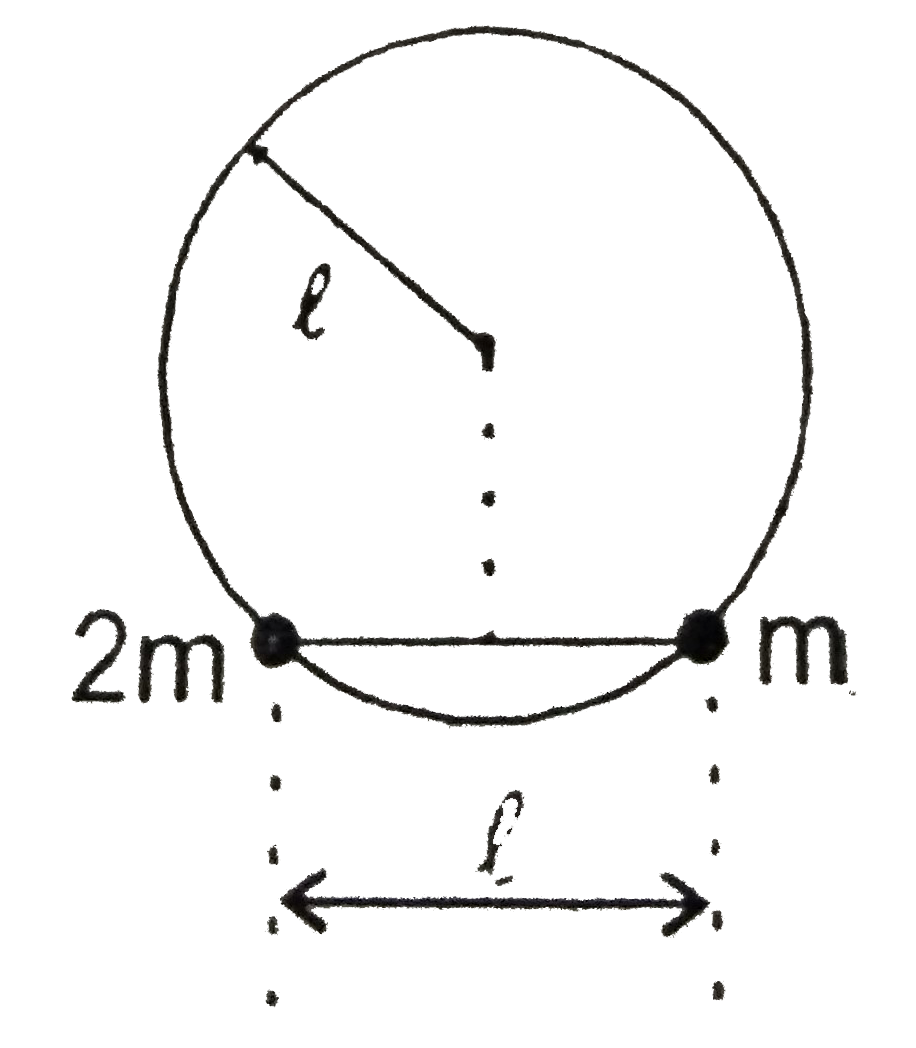
The minimum velocity that should be given to the mass 2m in clockwise direction to make it vertical is :A√5gl3B√7gl3C ⎷(3√3−13)glDnone of theseTwo beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )
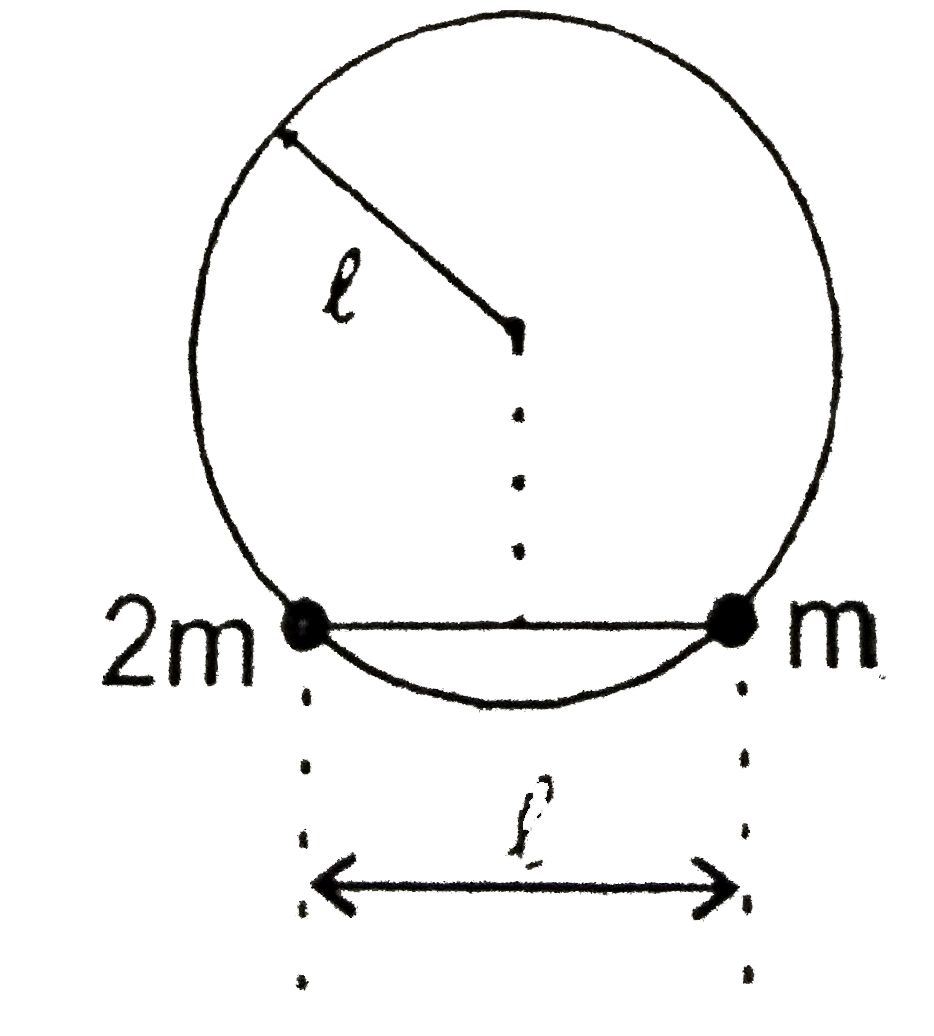
The velocity that should be given to mass 2m( when rod is in horizontal position ) in counter − clockwise direction so that the rod just becomes vertical is :A√5gl3B ⎷(3√3−13)glC√32glD√52glA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 A3g2lB3glCg2lD2gl
A3g2lB3glCg2lD2gl
Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
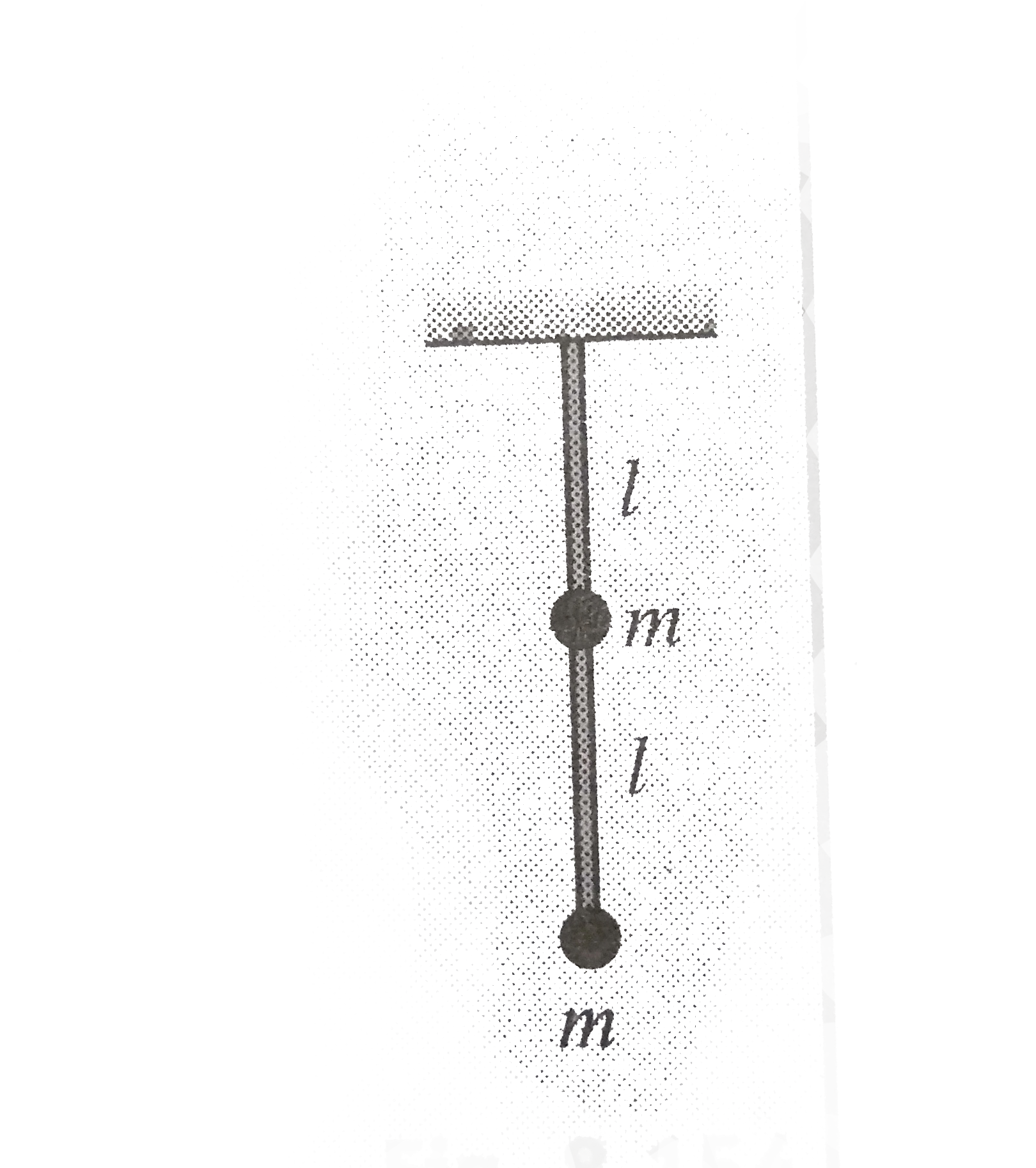
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
View Solution
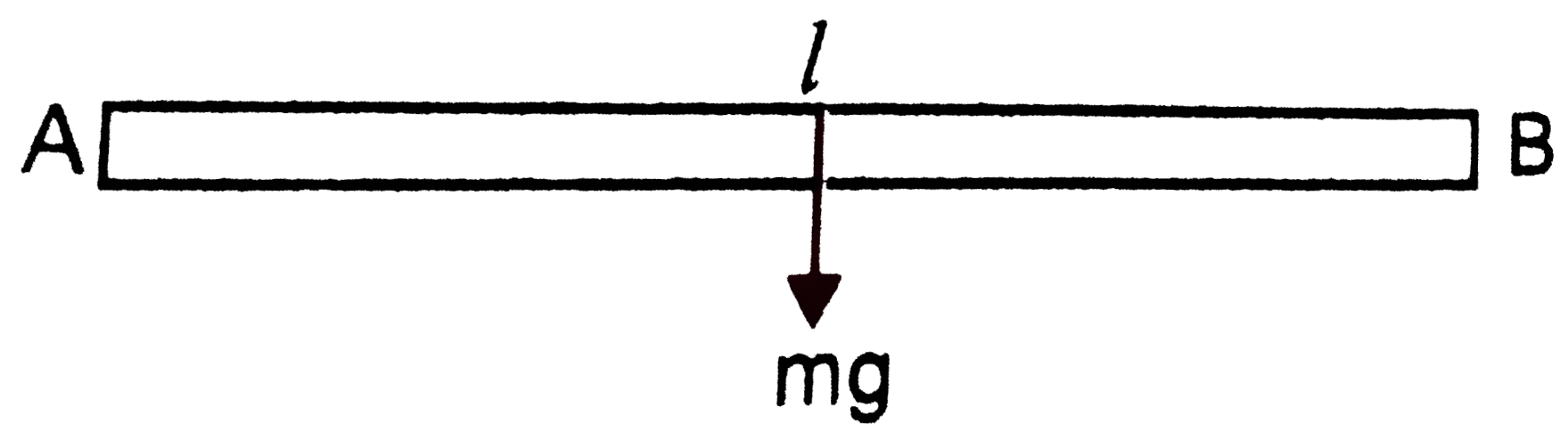
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionTwo small rings each of mass 'm' are connected to a block of same mass 'm' through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings make an angle of θ=60∘ with vertical is. (Take g=10m/s2)

View SolutionTwo blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.

View Solution
