A man of mass 60kg is standing on a platform executing SHM in the vertical plane. The displacement from the mean position varies as y=0.5sin(2πft). The value of f, for which the man will feel weightlessness at the highest point, is (y in metre)
g4π
4πg
√2g2π
2π√2g
The correct Answer is:C
If he feels weightlessness then at the highest point, acceleration must be g.
⇒g=ω2A
⇒ω=2πf=√2g
⇒f=√2g2π
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 71
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 72
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 69
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A horizontal platform with a mass of 100kg rotates at 10(r±) around a vertical axis passing through its centre. A man of mass 60kg is standing on its edge. The platform begins to rotaté with an angular velocity ω(r±), if the man "moves from the edge of the platform to its centre. Regard the platform as a circular homogeneous disk and the man as a point mass. Find the value of 3ω11.
View SolutionA body of mass 0.1 kg performing linear SHM experiences a restoring force of 1 N when its displacement from the mean position is 5 cm. Find (i) the force constant (ii) the period of SHM (iii) the acceleration of the body, when its displacement from the mean position is 1 cm./
View Solution
Knowledge Check
The equation for the displacement of a particle executing SHM is x=5sin(2πt)cm Then the velocity at 3cm from the mean position is( in cm//s)
A2πB3πC4πD8πThe displacement of a particle from its mean position (in metre) is given by
y=0.2sin(10πt+1.5π)cos(10πt+1.5π)
The motion of the particle isAperiodic but not simple harmonic motionBnon-periodicCsimple harmonic motion with period of 0.1 sDsimple harmonic motion with period of 0.2 sThe displacement of a particle from its mean position (in mean is given by y=0.2sin(10πt+1.5π)cos(10πt+1.5π). The motion but not S.H.M.
APeriodic but not S.H.MBNone-periodicCSimple harmonic motion with period 0.1sDSimple harmonic motion with period 0.2s
A man of mass 50 kg is standing on one end of a stationary wooden plank resting on a frictionless surface. The mass of the plank is 100 kg its length is 75 m and the coefficient of friction between the man the plank is 0.2 Find the least possible time (in sec) in which the man reach the other end starting from rest and stopping at the other end.
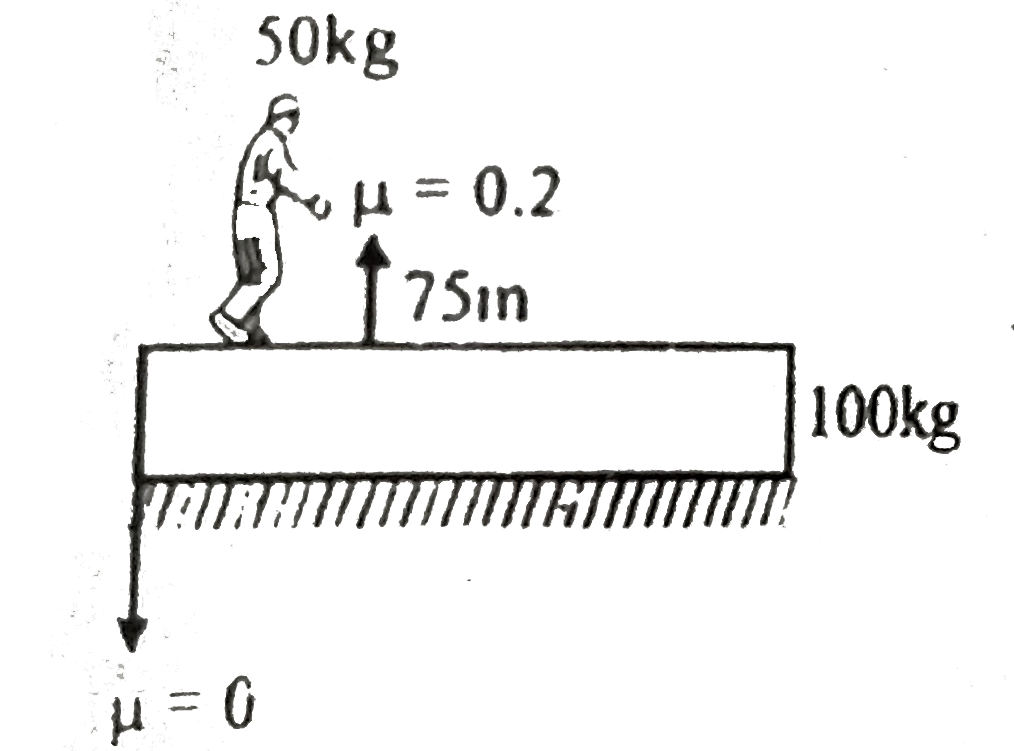
View SolutionA man of 80 kg mass is standing on the rim of a circular platform rotating about its axis. The platform with the man on it rotates at 12.0 r.p.m. How will the system rotate, if the man moves to the platform's centre? What work will the man perform in changing his position? The mass of the platform is 200 kg and its radius is 1.2 m.
View SolutionThe equation for the displacement of a particle executing SHM is y=5sin(2πt)cm. Find
(i) velocity at 3cm from the mean position
(ii) acceleration at 0.5s after having the mean position
View SolutionThe displacement of a particle from its mean position (in metre) is given by
y=0.2sin(10πt+1.5π)cos(10πt+0.5π).
The motion of particle is
View SolutionA man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is
View Solution
