
In given diagram what is the minimum value of a horizontal external force F on block A so that block B will slide on ground is .
30N
20N
10N
Not possible
The correct Answer is:D
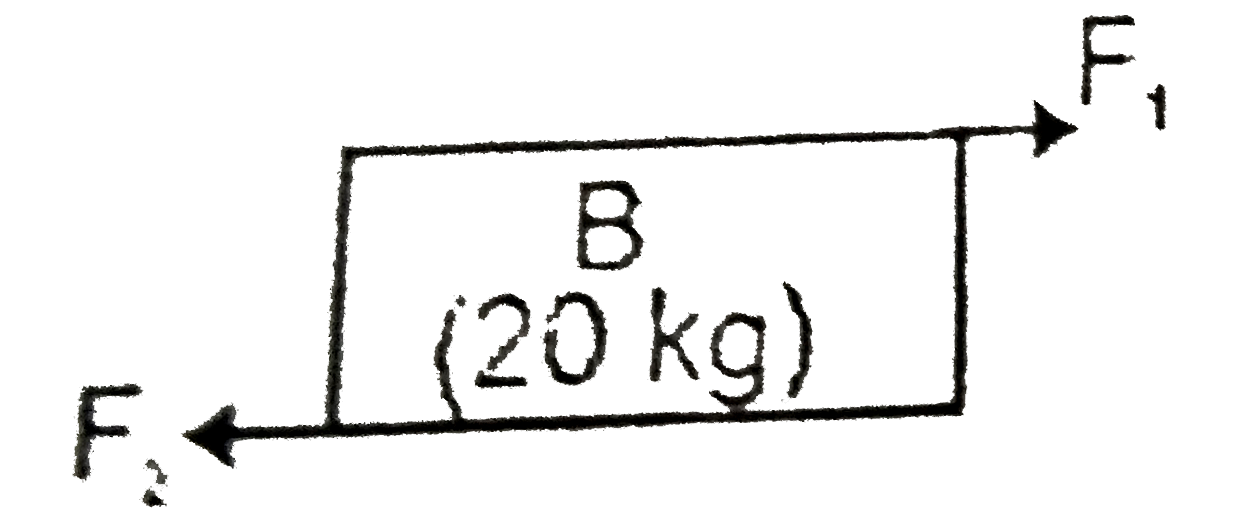
F1(max)=0.2×10×10=20N
F2(max)=0.1×30×10=30N
F1(max)<F2(max)
⇒'B' can never move.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 724videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp734videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 707videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
Four block are arranged on a smooth horizontal surface as shown in figure .The masses of the blocks are given (see the fig ) The coefficient of static friction between the top and the bottom blocks is μs What is the maximum value of the horizontal force F applied to one of the bottom blocks as shown that makes all four block with the same acceleration ?
 View Solution
View SolutionFour blocks are arranged on a smooth horizontal surface as shown. The masses of the blocks are given (see the diagram). The coefficient of static friction between the top and the bottom blocks is μs. What is the maximum value of the horizontal force F, applied to one of the bottom blocks as show, thilt makes all four blocks move with the same acceleration ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
Ag(cosθ+μsinθsinθ−μcosθ)Bg(sinθ+μcosθcosθ−μsinθ)Cg(sinθ−μcosθsinθ+μcosθ)Dg(cosθ−μsinθsinθ+μcosθ) - Question 2 - Select One
Two blocks A and B are as shown in figure. The minimum horizontal force F applied to the block B for which slipping behins between B and ground is :
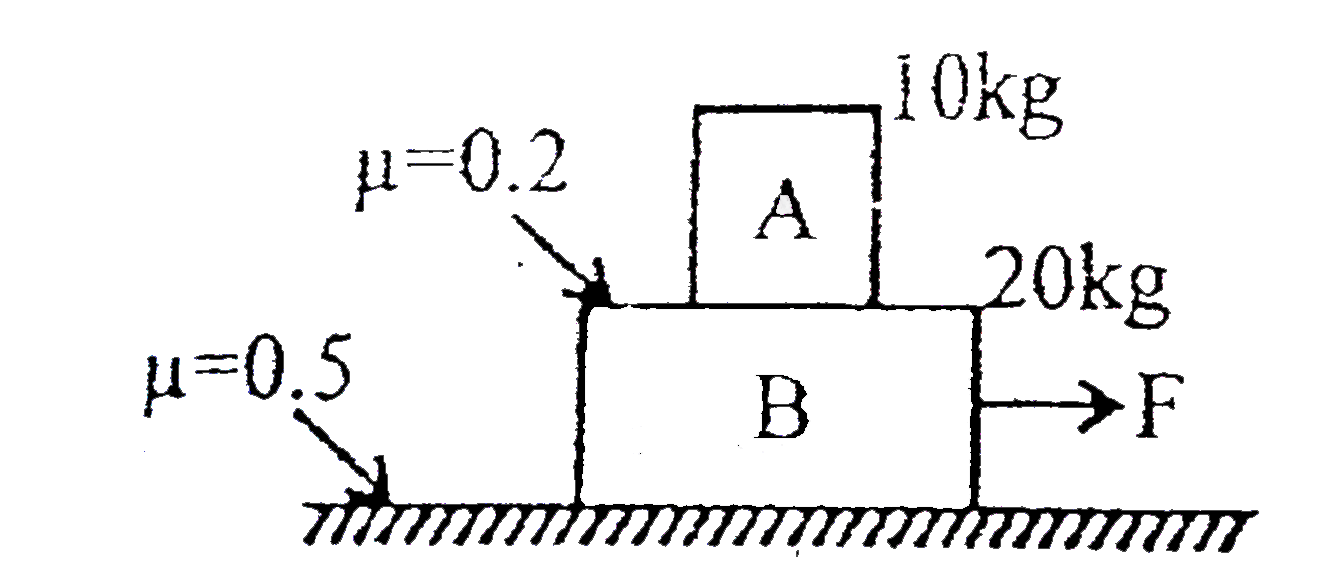 A20NB120NC150ND170N
A20NB120NC150ND170N - Question 3 - Select One
Two block A and B are as shown in figure. The minimum horizantal force F applied to the block B for which slipping begins between B and ground is :
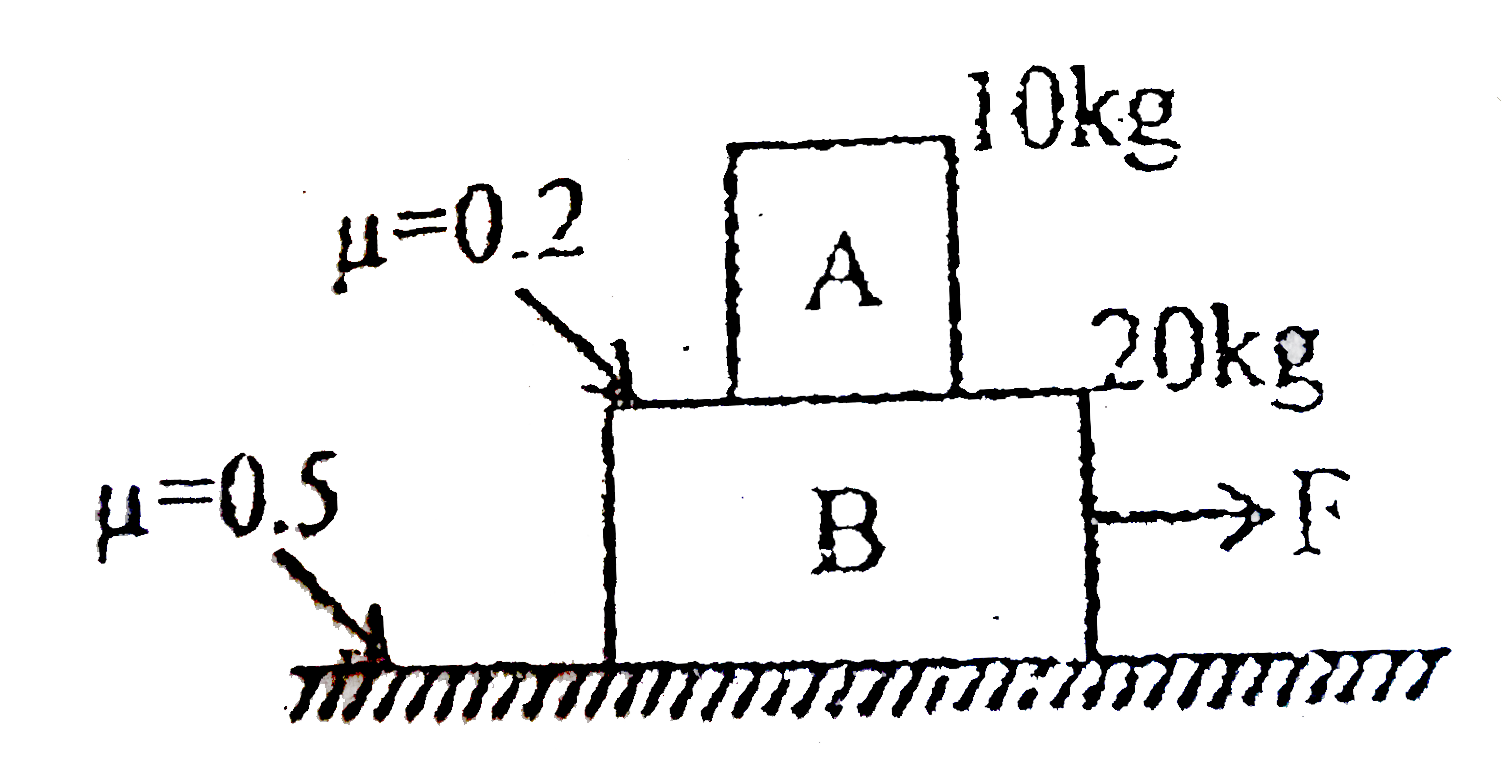 A20NB120NC150ND170N
A20NB120NC150ND170N
A bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block
 View Solution
View SolutionFigure-2.202 shows a two block constrained motion system. Block A has a mass M and B has a mass m. If block A is pulled toward right horizontally with an external force F, find the acceleration of the block B relative to ground.
 View Solution
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
 View Solution
View Solution
Two blocks A and B are shown in figure. The minimum horizontal force F applied on Blocks B for which slipping begins at B and ground isView SolutionIn the previous quiestion the minimum force F required so that block A will slip on block B is:
View Solution

