If a convex lens of refractive index μl is placed in a medium of refractive index μm Such that μl>μm>μair then
The nature of the lens is diverging
The nature of the lens is converging
The nalure of the lens may be converging or diverging
The nature of the lens can't be determined
The correct Answer is:B
To determine the nature of a convex lens placed in a medium with a higher refractive index than air, we can follow these steps:
Step 1: Understand the Properties of the Lens
A convex lens is characterized by its ability to converge light rays. The refractive index of the lens (μ_l) is greater than that of the medium (μ_m) in which it is placed, and both are greater than the refractive index of air (μ_air).
Step 2: Use the Lens Maker's Formula
The lens maker's formula relates the focal length (f) of a lens to its refractive indices and the radii of curvature of its surfaces. The formula is given by:
1f=(μlμm−1)(1R1−1R2)
Where:
- μl = refractive index of the lens
- μm = refractive index of the medium
- R1 and R2 = radii of curvature of the lens surfaces
Step 3: Analyze the Focal Length in Air
When the lens is in air, the focal length is positive since:
1f=(μlμair−1)(1R1−1R2)
Here, μl>μair implies that μlμair−1>0, leading to a positive focal length.
Step 4: Analyze the Focal Length in the Medium
Now, when the lens is placed in a medium with refractive index μm:
1f′=(μlμm−1)(1R1−1R2)
Given that μl>μm, we have μlμm−1>0. This means that f′ will also be positive.
Step 5: Conclusion
Since both focal lengths f and f′ are positive, the lens behaves as a converging lens in both cases. Therefore, the nature of the lens remains converging when placed in a medium with a refractive index lower than that of the lens.
Final Answer
The lens is a converging lens.
---
A convex lens is characterized by its ability to converge light rays. The refractive index of the lens (μ_l) is greater than that of the medium (μ_m) in which it is placed, and both are greater than the refractive index of air (μ_air).
The lens maker's formula relates the focal length (f) of a lens to its refractive indices and the radii of curvature of its surfaces. The formula is given by:
1f=(μlμm−1)(1R1−1R2)
Where:
- μl = refractive index of the lens
- μm = refractive index of the medium
- R1 and R2 = radii of curvature of the lens surfaces
When the lens is in air, the focal length is positive since:
1f=(μlμair−1)(1R1−1R2)
Here, μl>μair implies that μlμair−1>0, leading to a positive focal length.
Now, when the lens is placed in a medium with refractive index μm:
1f′=(μlμm−1)(1R1−1R2)
Given that μl>μm, we have μlμm−1>0. This means that f′ will also be positive.
Since both focal lengths f and f′ are positive, the lens behaves as a converging lens in both cases. Therefore, the nature of the lens remains converging when placed in a medium with a refractive index lower than that of the lens.
The lens is a converging lens.
Topper's Solved these Questions
Similar Questions
Knowledge Check
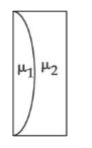
A thin symmettrical double convex lens of refractive index μ2−1.5 is placed between a medium of refractiv eindex μ1=1.4 to the left and another medium of refractive index μ3=1.6 to the right.Then the system behaves as
Aa convex lensBa concave lensCa glass plateDa convexo concave lensA double convex lens of glass of refraction index μ is immersed in a medium of refractive index μ1. If a parallel beam emerges undeviated through the lens, then
Aμ=μ1Bμ=1μ1Cμ>μ1Dμ<μ1A convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
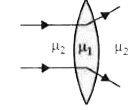 Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
A sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View SolutionA thin bi-convex lens made out of a material of refractive index μ1 is place in a medium of refractive index μ2. A paraxial beam of light, parallel to the principal axis of the lens, is shown in the figure. Based on the ray diagram, we can conclude that

View SolutionCurved surfaces of a plano-convex lens of refractive index μ1 and a plano-concave lens of refractive index μ2 have equal radius of curvature as shown in figure. Find the ratio of radius of curvature to the focal length of the combined lenses.
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View Solution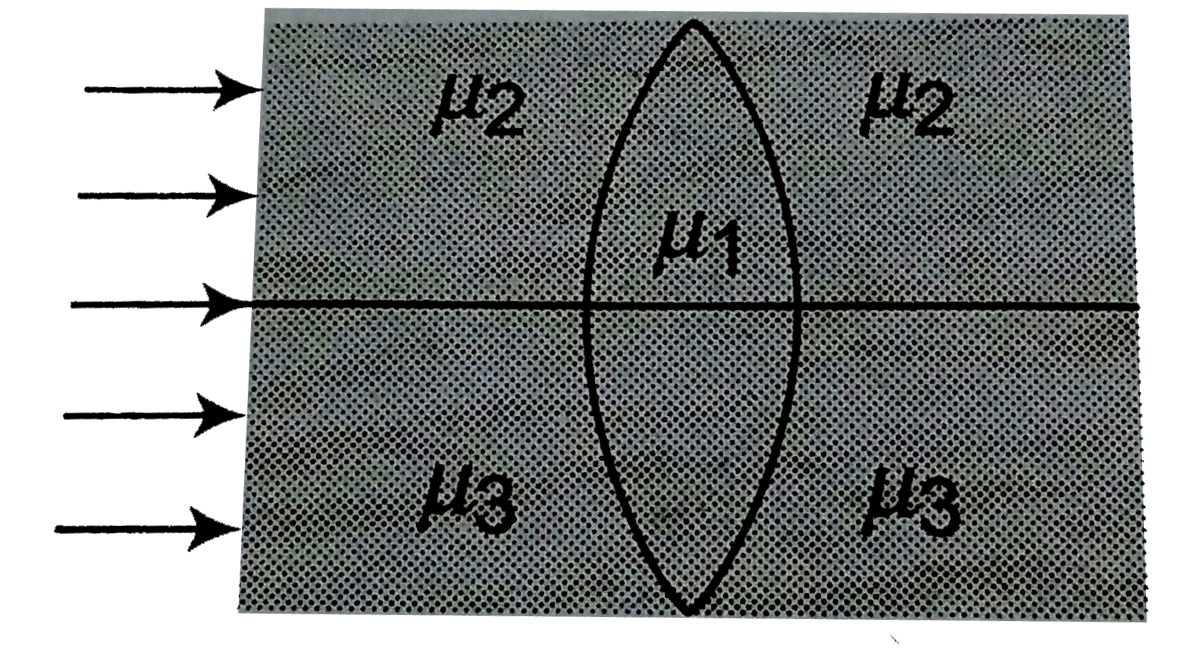
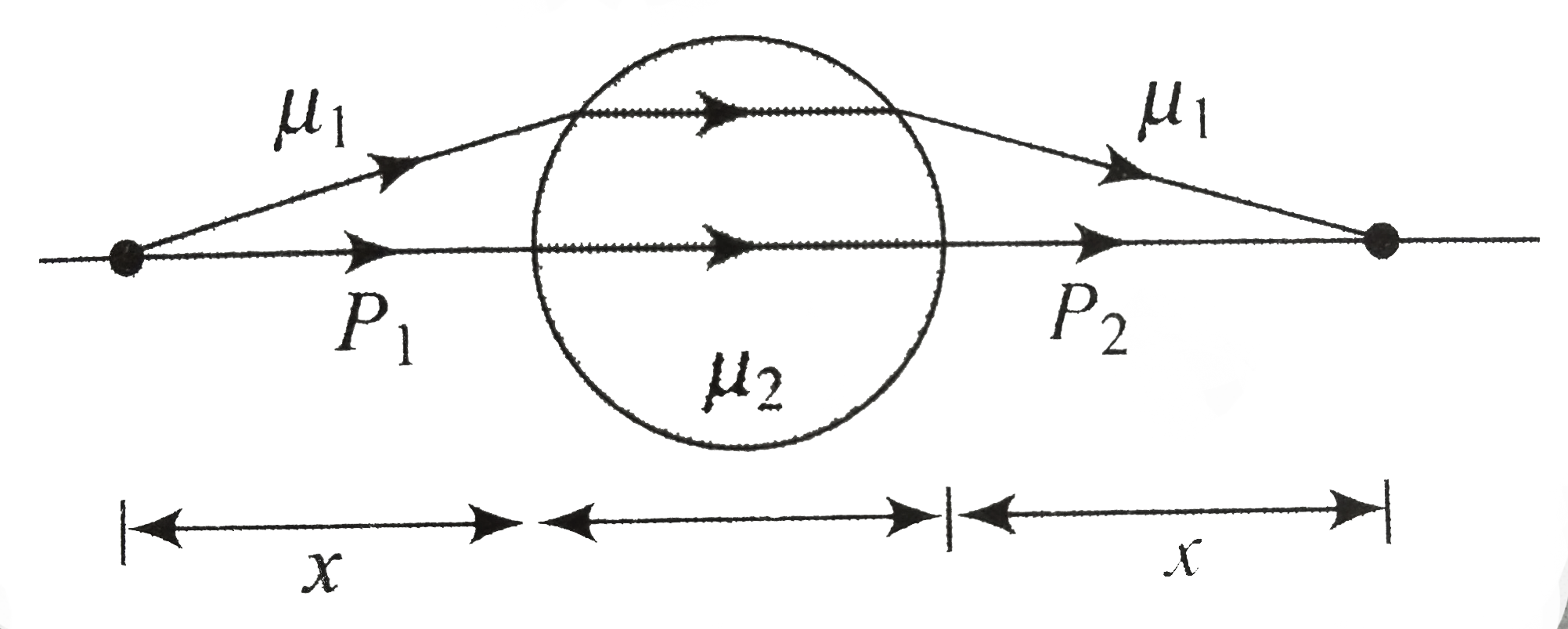
A double convex lens made of a material of refractive index μ1, is placed inside two liquids of refractive indices μ2 and μ3 as shown (μ1>μ2>μ3) A wide parallel beam of light is incident on the lens from the left. The lens will give rise to
View Solution

 .
.