A glass beaker has diameter 4cm wide at the bottom. An observer observes the edge of bottom when beaker is empty as shown in figure. When the beaker is completely filled with liquid of refractive index n=√5/2, he can just see the centre of bottom, then the height of glass beaker is :

4cm
√5/2cm
16cm
None of these
The correct Answer is:A
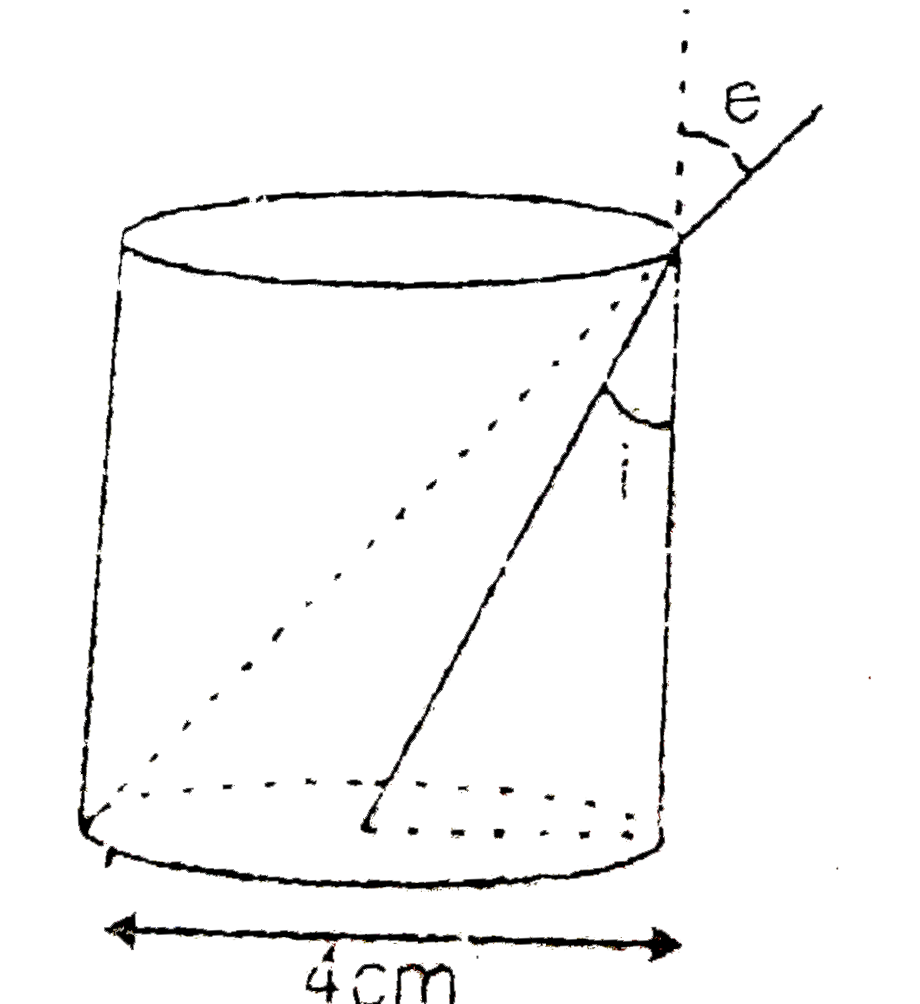
√52sini=1sine
⇒√522cm√4cm2+h2=1×4cm√16cm2+h2
⇒h=4cm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.14
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.15
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.12
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A rod of height h is palced in a beaker of same radius. The height of the beaker is 3 times its radius. An observer sees the top end of the rod through a pin hole. When the beaker is filled with a liquid of refractive index √μ upto a height 2h, he can see the lower end of the rod. Find the value of μ
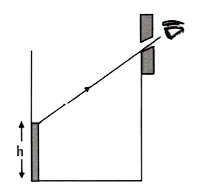
View SolutionIf an observer sees the bottom of the vessel shown in Figure., at 8cm, find the refractive index of the medium in which the observer is present.

View Solution
Knowledge Check

A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be movedAdownward by 2 cmBupward by 2 cmCdownward by 3 cmDupward by 3 cmA converging glass lens with a refractive index of 1.5 has a focal length of f in air. When it is completely immersed in a liquid of refractive index 2, its focal length and nature will be respectively
A2f and covergingB3f and convergingC2f and divergingD3f and divergingAn observer can see through a pin-hole the top end of a thin of height h, places as shown in figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 A52B√52C√32D32
A52B√52C√32D32
A person looking through a telescope T just sees the points on the rim at the bottom of a cylindrical vessel when the vessel is empty. When the vessel is completely filled with a liquid (μ,=1.5), he observes a mark at the centre B,of the bottom without moving the telescope or the vessel. What is the height of the vessel if the diameter of it scross section is 10cm.
View SolutionConsider a tin can of height h as shown in the figure. A coin lies on the botttom at the centre. From the position shown you can barely see the far side of the bottom of the can. When the can is slowly filled with water of refractive index μ, coin is just visible when the can is full. Show that the ratio of the height to radius is
hr=2√μ2−14−μ2

View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
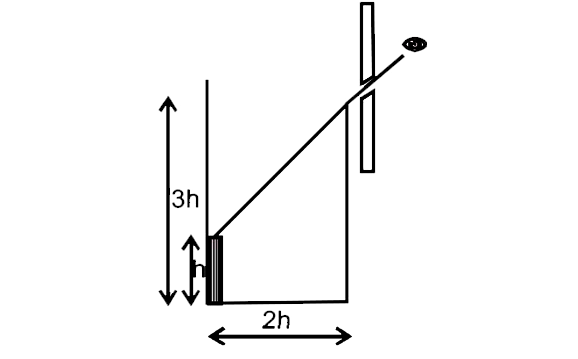
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
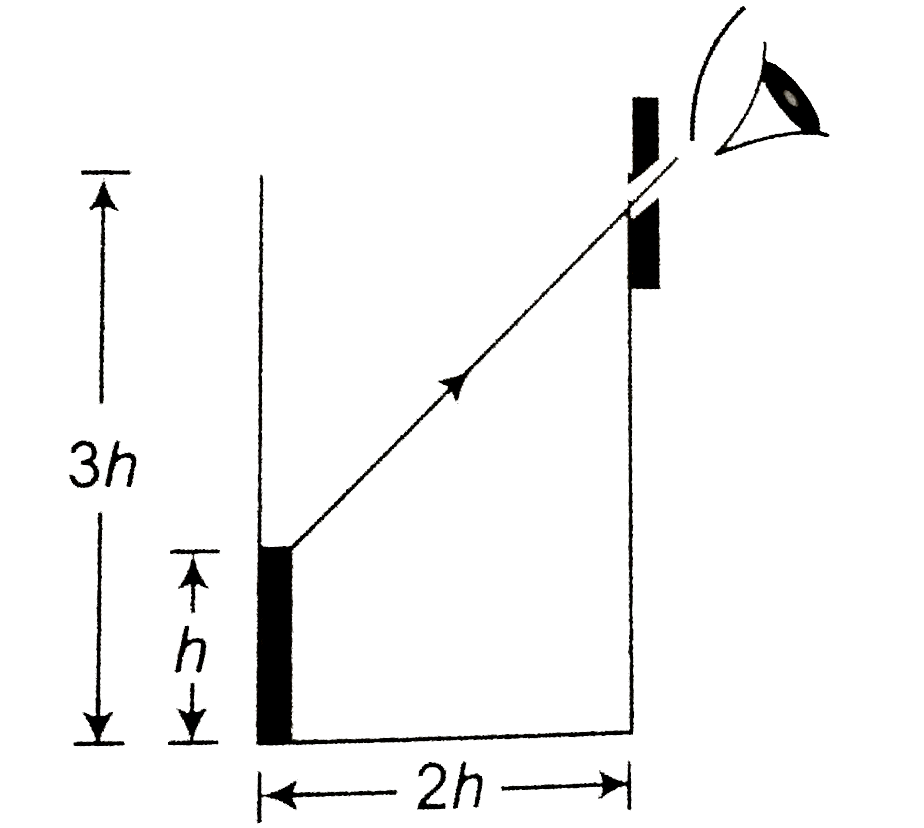
View Solution
