A horizontal cylinder is fixed, its inner surface is smooth and its radius is R. A small block is initially at the lowest point. The minimum velocity that should by given to the block at the lowest point, so that it can just cross the point P is u then
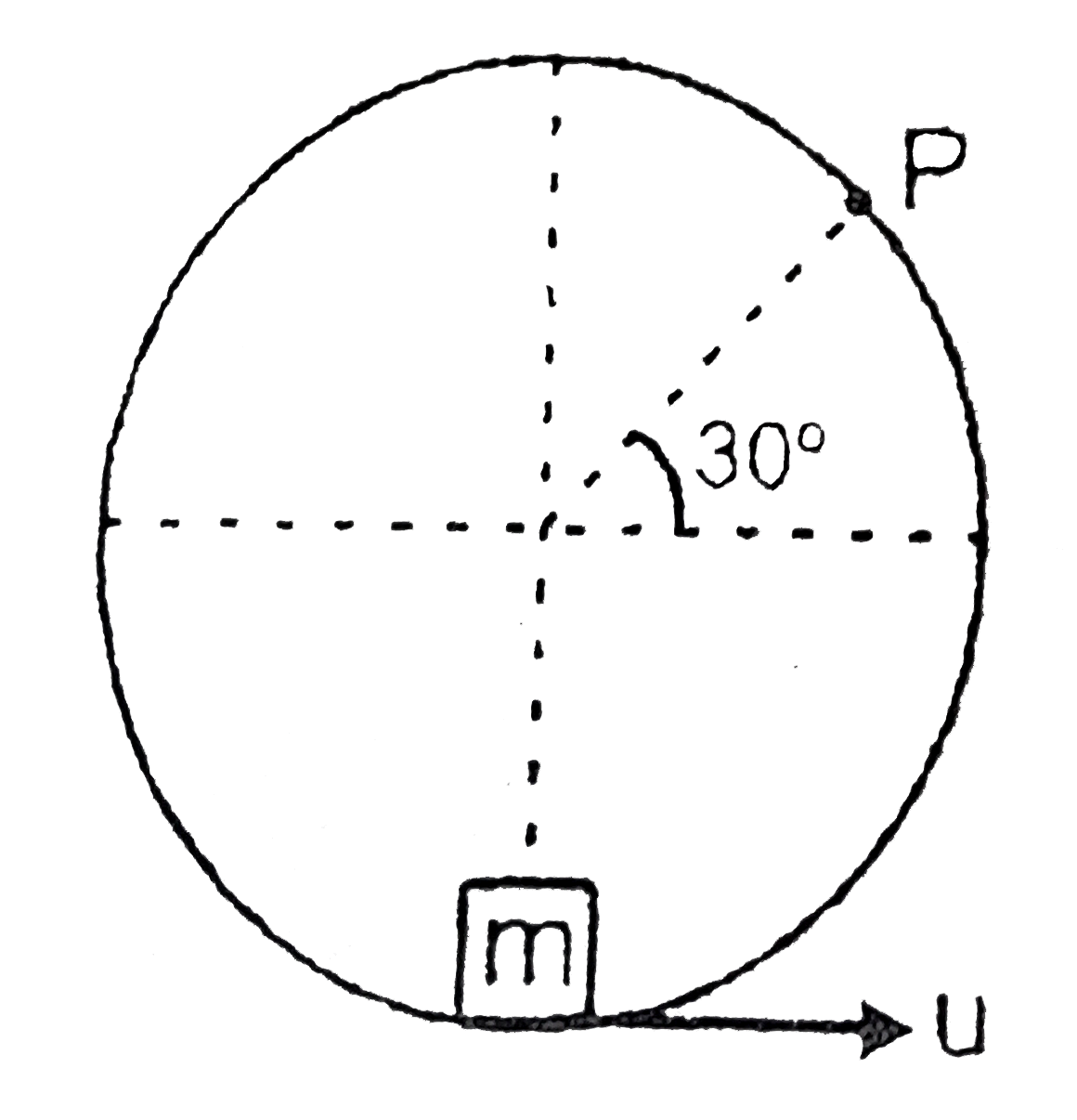
If the block moves anti clockwise then u=√3.5gR
If the block moves anti clockwise then u=√3gR
If the block moves clockwise then u=√3.5gR
If the block moves clockwise then u=√5gR
The correct Answer is:A, D
N=μ2R+mg(3cosθ−2), at θ=120∘N
=0⇒N=mu2R+mg(3cos120∘−2)=0
⇒u=√3.5gR
If the block is moving clockwise, then to cross the point P, the block has to cross the highest point, so to cross the highest point
=√5gR.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3320videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.349videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3120videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II
 View Solution
View SolutionA track (ACB) is in the shape of an arc of a circle. It is held fixed in vertical plane with its radius OA horizontal. A small block is released on the inner surface of the track from point A. It slides without friction and leaves the track at B. What should be value of q so that the block travels the largest horizontal distance by the time it returns to the horizontal plane passing through B?
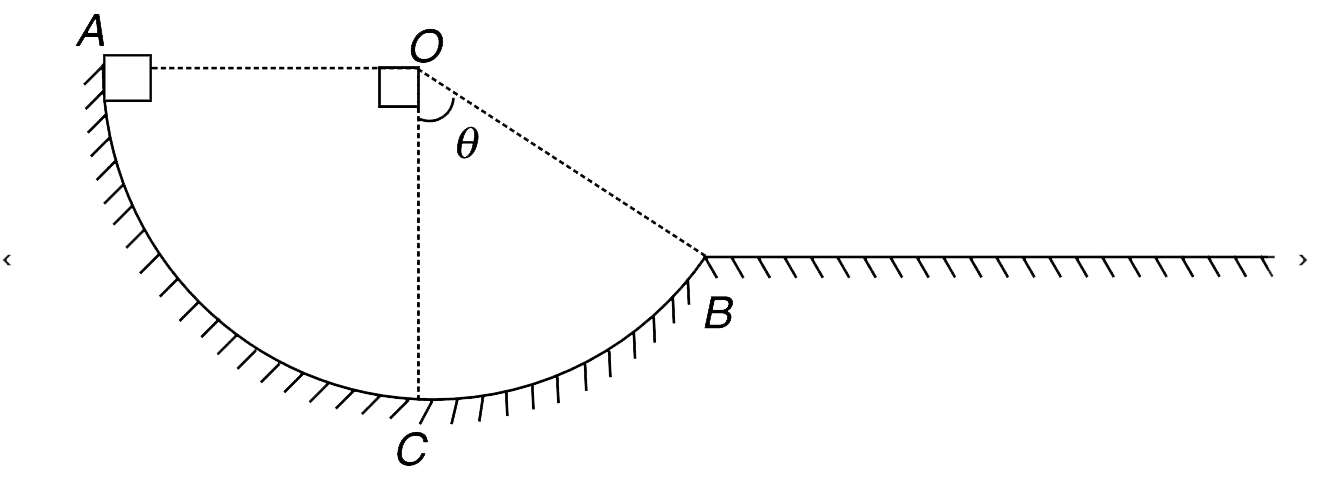 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
A√glB√3glC√5glD√7gl - Question 2 - Select One
Figure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
What minimum velocity should be imparted to a small block of same mass m so that it may each point B :
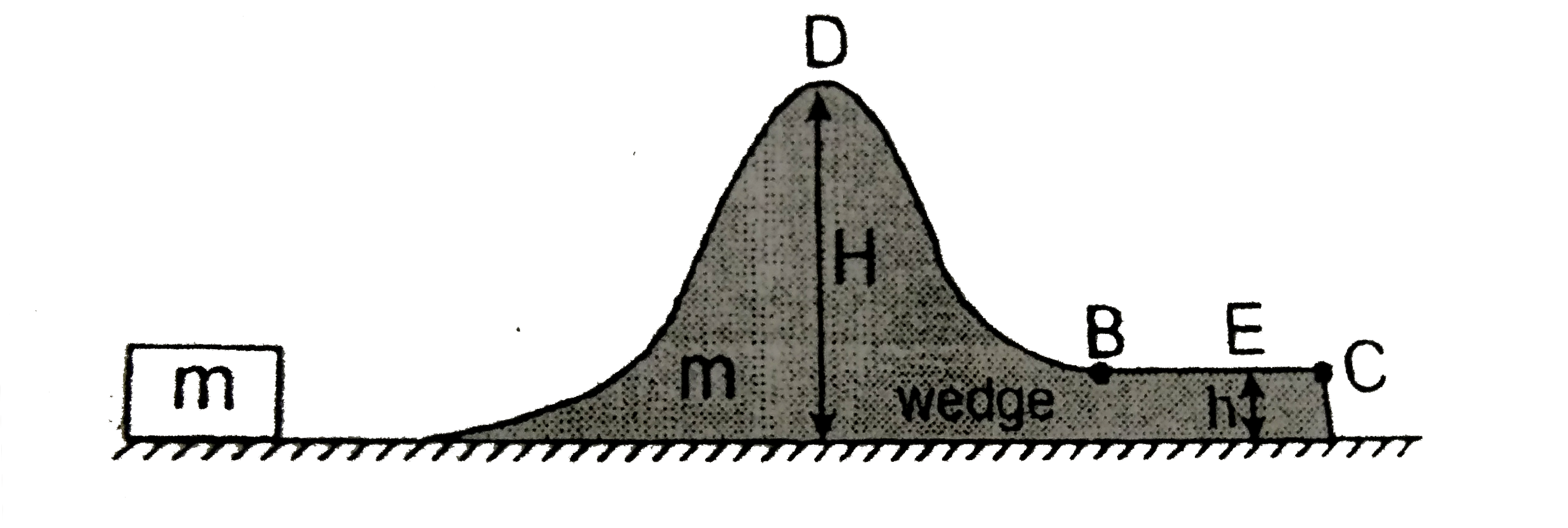 A2√gHB√2gHC2√g(H−h)D√gh
A2√gHB√2gHC2√g(H−h)D√gh - Question 3 - Select One
A point mass m is moved in vertical circle of radius r with help of string. Velocity of mass is 7gr√ at lowest point. Tension in string at lowest point is
A7 mgB8 mgC1 mgD6 mg
A particle is projected along the inner surface of a smooth vertical circle of radius R, its velocity at the lowest point being (1/5)(√95gR). If the particle leaves the circle at an angular distance cos−1(x/5) from the highest point, the value of x is.
View SolutionA small ball of mass m having charge q is suspended by a string of length L. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity which should be imparted to ball at lowest point so that it can make complete revolution.
View SolutionParticle slides down the surface of a smooth fixed sphere of radius r starting from rest at the highest point. Find where it will leave the sphere. Show that it strike the horizontal plane through the lowest point of the sphere at a distance equal to 5[√5+4√2](r/27) from the vertical diameter.
View SolutionIn the above question, the velocity of the image of Q in plane mirror of block P with respect to ground when Q is at the lowest point first time is:
View Solution
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?View Solution

