A cylindrical wooden float whose base area S and the height H drift on the water surface. Density of wood d and density of water is ρ. What minimum work must be performed to take the float out of the water ?
The correct Answer is:Sgd2H2
Applying Newton's law vertical direction

mg=FB
⇒dSH×g=ρwSh×g
⇒h=dHρ
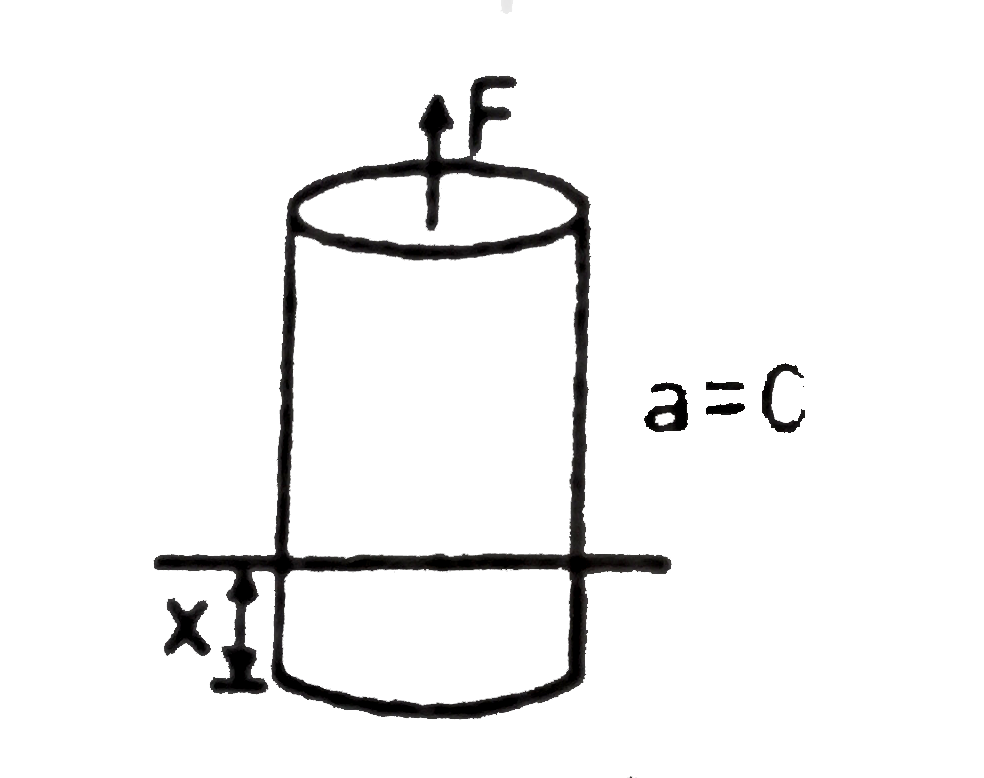
Now when force F is applied, for minimum work a
= 0 (∵ for a =0, F is minimum)
F−mg+ρS×g=0
F=mg−ρS×g
W=∫Fdx=∫(mg−ρS×g)dx
=mg∫dx−ρSg∫xdx
W=mgh−ρSgh22=(ρSh)gh−ρSgh22
=ρSgh22=ρSg2(dHρ)2=Sgd2H22ρ
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.42
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.43
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.40
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A cylinder wooden float whose base area S=4000cm2 & the altitude H=50cm drifts on the water surface specific weight of wood d=0.8gf/cm3
(i). What work must be performed to take the float out of the water?
(ii). Compoute the work to be performed to submerged completely the float into the water.
View SolutionA solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water).

(a) Find tension in the string.
(b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p0.
View Solution
Knowledge Check
A solid floats such that its 1/3 part is above the water surface. Then, the density of solid is
A744kgm−3B10003kgm−3C20003kgm−3D910kgm−3A wooden sylinder floats vertically in water with half of its length immersed. The density of wood is:
Aequal to that of waterBhalf the density of waterCdouble the density of waterDthe quiestion is incomplete.A block of wood floats with 1//4 of its volume under water. What is he density of wood? (Density of water =1000kg/m3)
A750kg/m3B250kg/m3C300kg/m3D260kg/m3
A log of wood floats in water with 15 of its volume above the surface. What is the density of wood?
View SolutionA block of ice with an area A and a height h floats in water of density ρ0. What work should be performed to submerge the ice block completely into water if density of ice is ρ1 ?
View SolutionA body is floating in water with 3/5th of its volume below the water surface. What will be density of the body?
View SolutionA cylindrical body floats in water such that one-fourth of its volume lies above the surface of water. Find the density of the meterial with which the body is made of.
View SolutionA block of wood floats with34th of its volume submerged in water. The density of wood is ________
View Solution
