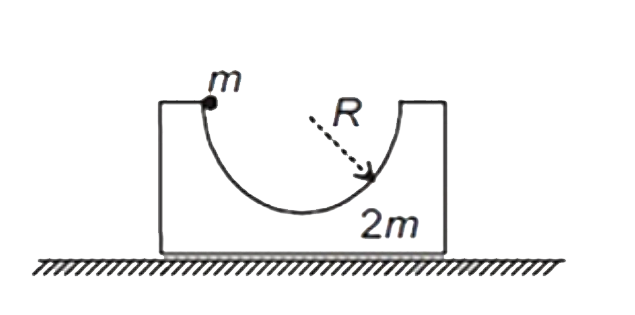
A solid ball of mass m and radius R is released from the position shown in a large hollow shell of same mass m and radius 3R as shown in figure. The displacement of the centre of mass of the system from its initial position when the solid ball ball touches the lower surface of the hollow shell is : (centres of both the spheres coincide intially) :

0
3R
2R
R
The correct Answer is:D
Initially coordinate of centre of mass is (0,0)
When solid ball touches the lower surface of hollow surface
VCm=M(2R)+mx0m+m=R
So finally coordinate of COM (0,R) displacement is (R-0) = R.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.599videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.609videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.579videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Three solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
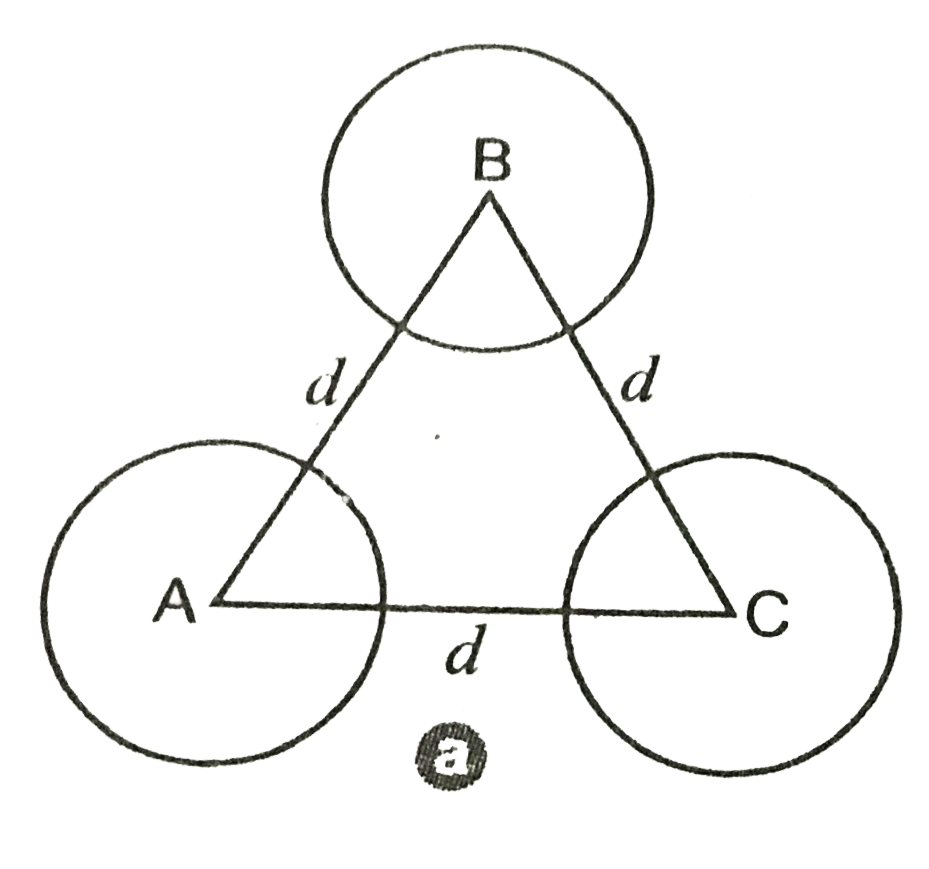 View Solution
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View Solution
Knowledge Check
- Question 1 - Select One
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3 - Question 2 - Select One
Three solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
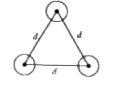 A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d) - Question 3 - Select One
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
Three solid spheres of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionLocate the position of the centre of mass of a hemisphere of radius R as shown in the following figure:
 View Solution
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
 View Solution
View SolutionA ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .View Solution
.View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2rView Solution

