A solid cylindrical pulley of mass m and radius R=10cm is hinged about its horizontal axis of symmetry. A light spring is wrapped around it, and small block of mass 'm' is suspended from the string. Now the block is lefted vertically by a distance h = 1.8 m and released. Just after the string becomes taut again, find the angular velocity of the cylinder in rad/s (Take g=10m/sec2)

The correct Answer is:40
Applying angular momentum conservation about the hinge point, between just before and just after the jerk
Li=Lf
(m)(√2gh)(R)=(m)(ωR)(R)+(mR22)ω
ω=23√2ghR→ω=23√2×10×1.80.1
ω=40rad/sec
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.639videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6420videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6120videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A horizontal, homogeneous cylinder of mass M and radius R is pivoted about its axis of symmetry. A string is wrapped several times around the cylinder and tied to a body of mass m resting on a support positioned so that the string has no slack. The body of mass m is then lifted vertically to a distance h, and then released.
(a) Evaluate the angular velocity ω0 of the cylinder, the speed v0 of the falling body of mass m, and the kinetic energy K0 of the system, just before the string becomes taut.
(b) Evaluate the corresponding quantities, ω1,v1,andK1, for the instant just after the string becomes taut.View SolutionA string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
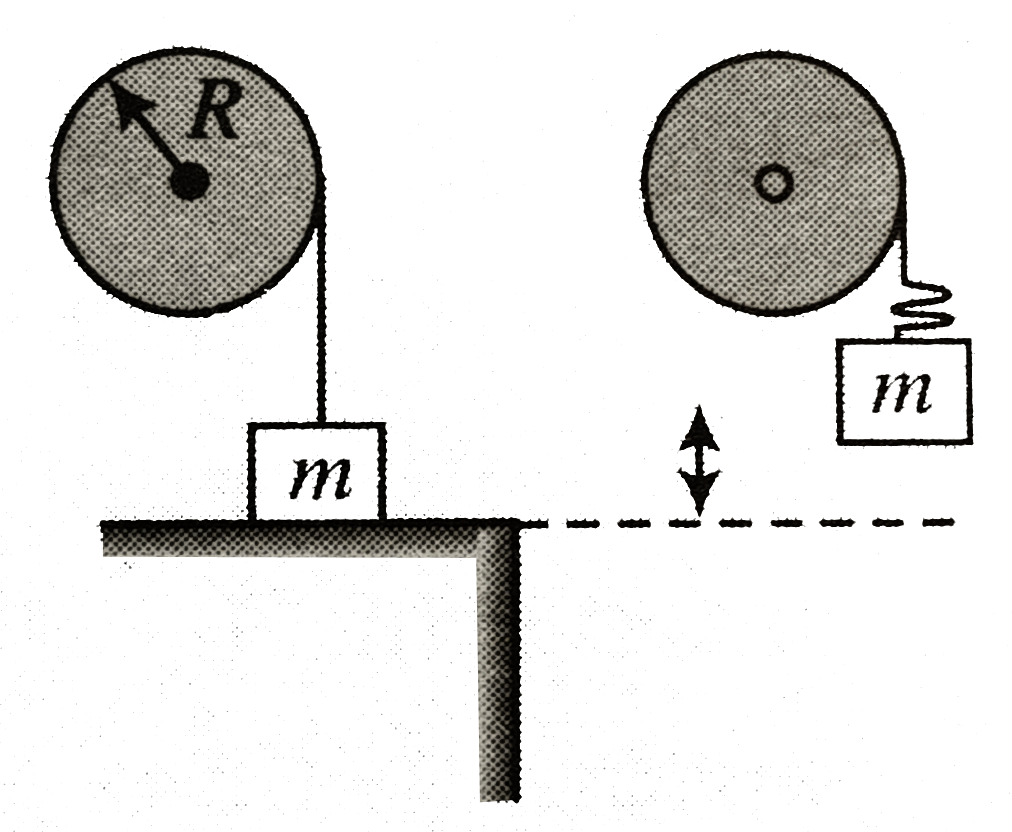 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
A2MM+2mgB2mM+2mgCM+2m2MgD2M+m2Mg - Question 2 - Select One
A block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is 1. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
 A√glR3B√gl2R2C√2gl3R2D√3gl2R2
A√glR3B√gl2R2C√2gl3R2D√3gl2R2 - Question 3 - Select One
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A2Mg/3BMg/2CMg/3DMg/6
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
 View Solution
View SolutionA 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m/s2)
 View Solution
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
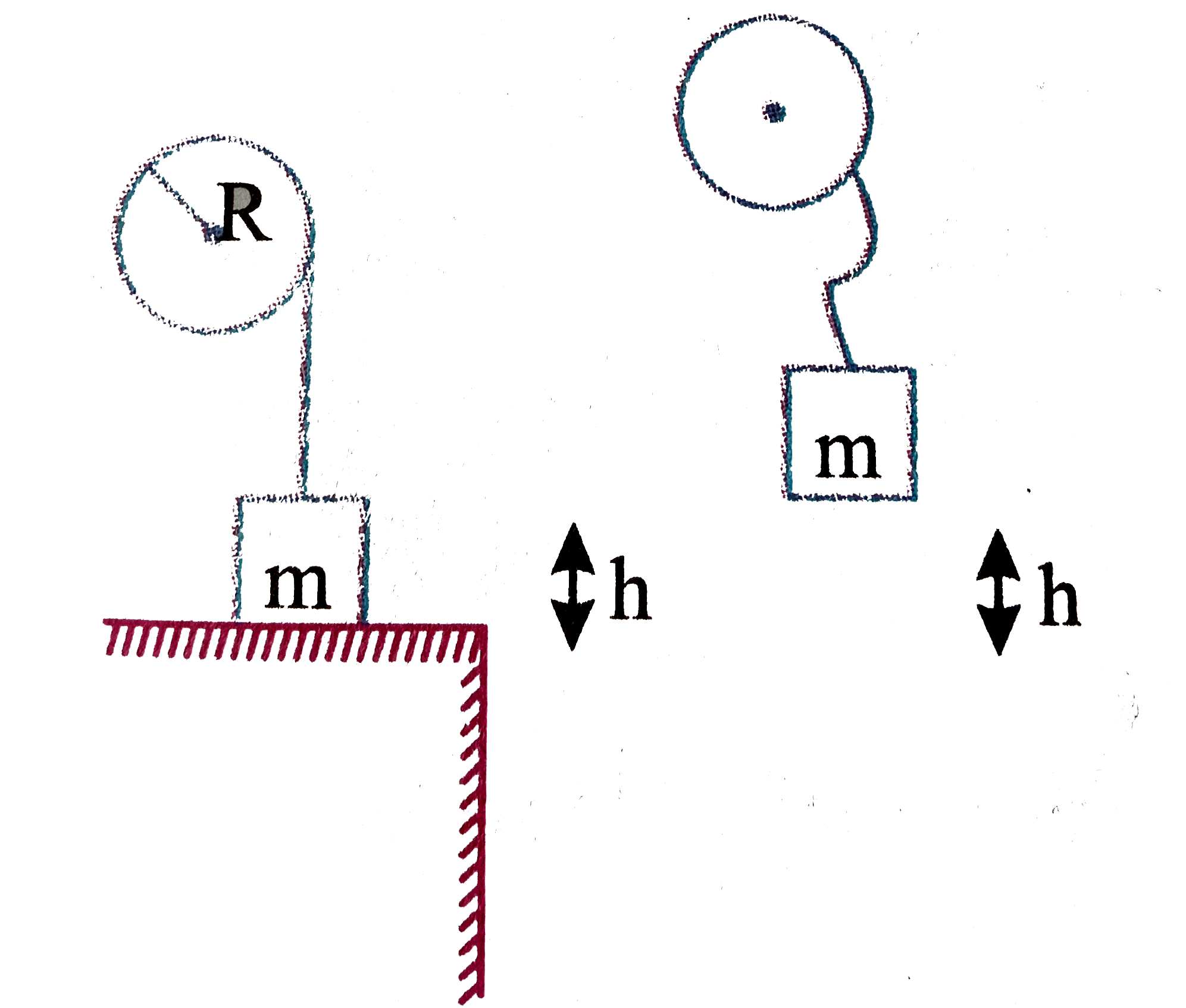
What is the angular velocity of cylinder just before the string becomes tautView Solution

