S2 is a fixed rough sphere and S1 is a uniform solid sphere S1 is given a negligible velocity, So that at starts moving on the sphere S2, It rolls without slipping. Find the angle formed with the vertical, by the line joining the centres of S1 and S2 when S1 leaves S2
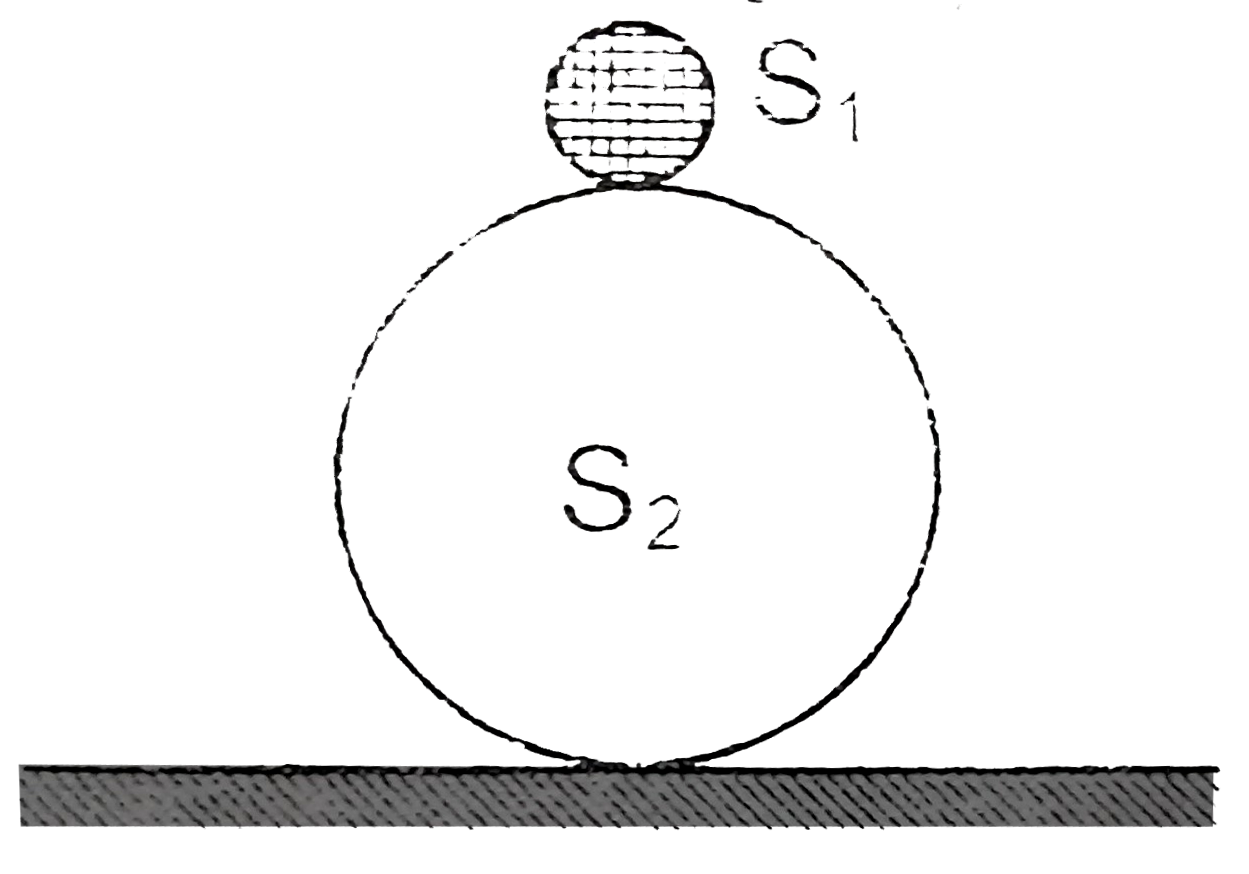
The correct Answer is:θ=cos−1(1017)
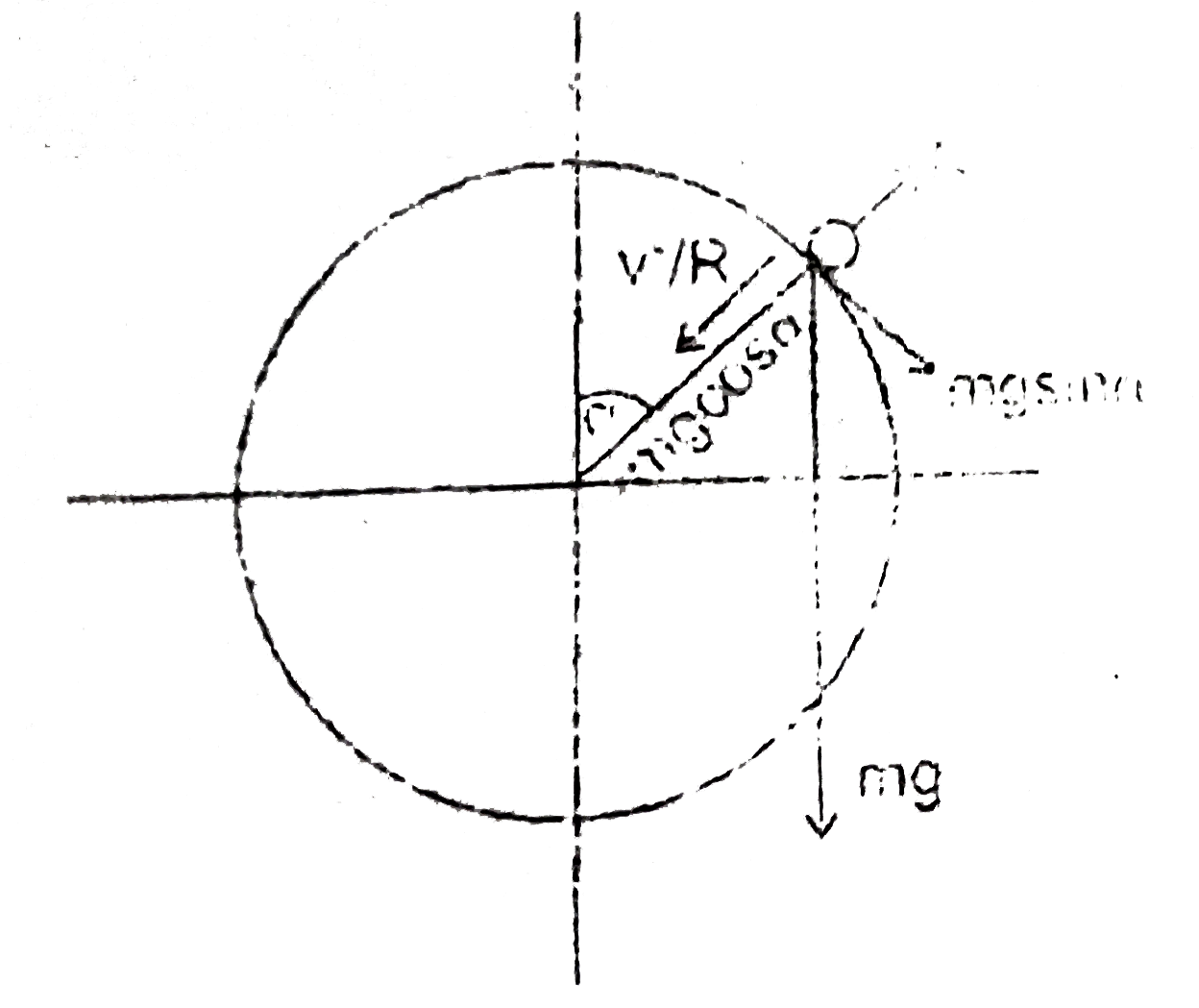
When sphere leaves constant N=0
Mgcosα−N=mv2R
⇒mgcosα=mv2R ….(i)
By energy conservation
Ki+U=K+Uf
0+mgR(1−cosα)=12mv2+12tω2
⇒MgR(1−cosα)=710mv2
(∴T+2/5mR2andv=ω)
⇒mgR=1710mgRcosα
⇒cosα=1017⇒α=cos−1(1017)
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.639videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6420videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6120videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ration of electric flux through S1andS2,
View SolutionS1andS2 are two concentric sphere enclosing charges 2Q and 3Q respectively as shown in the figure. What is the ratio of the electric flux through S1andS2?
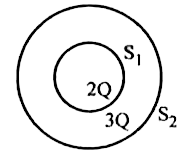 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If a solid sphere of mass 500 gram rolls without slipping with a velocity of 20 cm/s, then the rolling kinetic energy of the sphere will be
A140 JB280 JC0.014 JD0.028 J - Question 2 - Select One
A solid sphere of mass 500 gm and radius 10 cm rolls without slipping with the velocity 20cm/s. The total kinetic energy of the sphere will be
A0.028 JB280 JC140 JD0.014 J - Question 3 - Select One
If a solid sphere of mass 1 kg and radius 0.1 m rolls without slipping at a uniform velocity of 1 m/s along a straight line on a horizontal floor, the kinetic energy is
A75JB25JC710JD1 J
The sets S1 and S2 are given by
View SolutionA solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
View SolutionA solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
View SolutionA square S1 encloses another square S2 in such a manner that each corner of S2 is at the mid-point of the side of S1 . If A1 is the area of S1 and A2 is the area of S2 , then A1=4 A2 (b) A1=2 A2 (c) A2=2 A1 (d) A1=A2
View SolutionCharge q on a small conducting sphere S1 is placed inside a large hollow metallic sphere S2 having a charge Q as shown in figure. The sphere is connected to shell by a conducting wire. The charge on S1 will then be
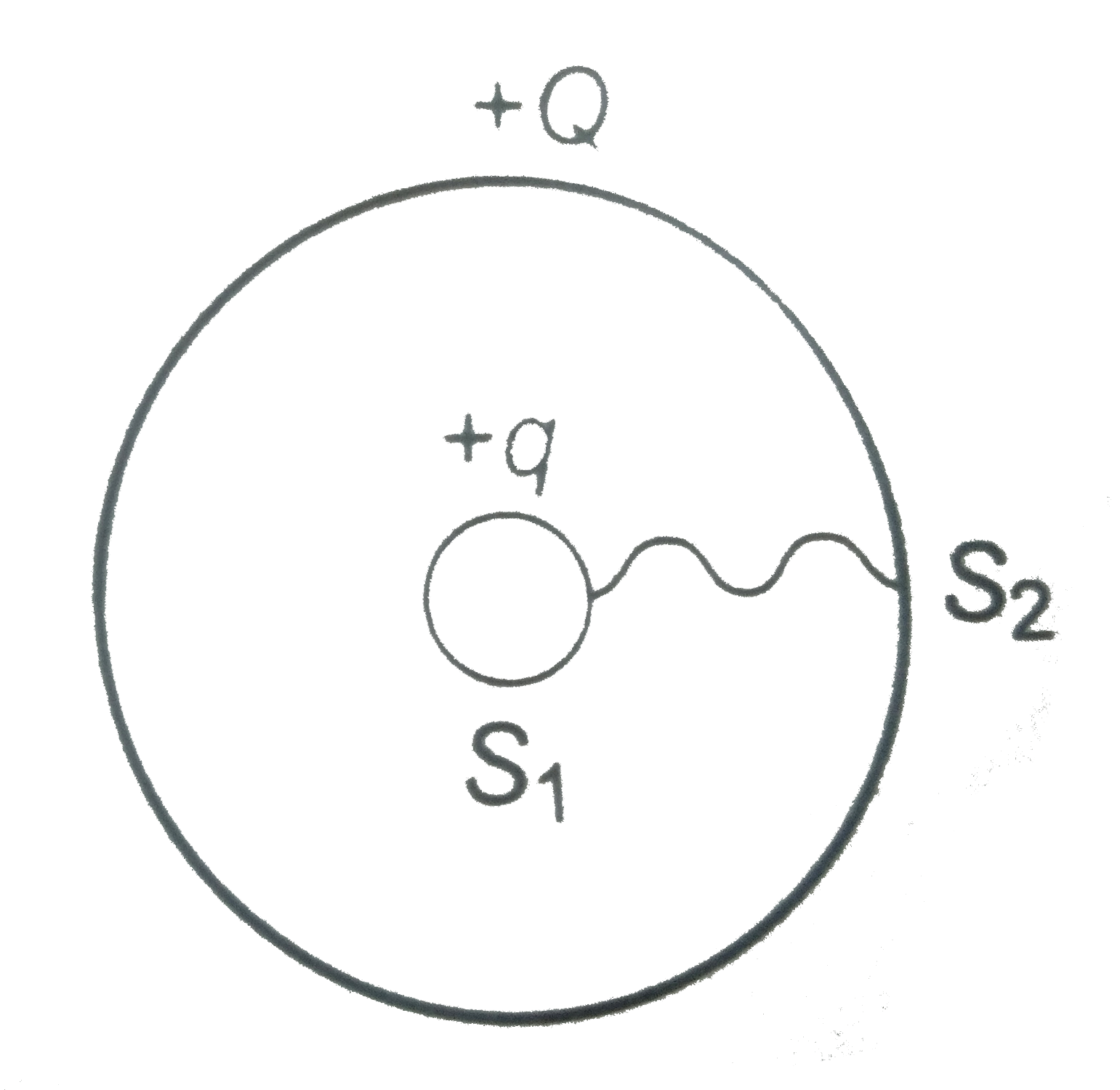 View Solution
View Solution

