Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
103m/s
107m/s
112m/s
123m/s
The correct Answer is:A
To find the speed of the center of mass of the system consisting of two particles, we can use the formula for the speed of the center of mass (V_cm) given by:
Vcm=m1v1+m2v2m1+m2
where:
- m1 is the mass of the first particle,
- v1 is the speed of the first particle,
- m2 is the mass of the second particle,
- v2 is the speed of the second particle.
1. Identify the masses and velocities:
- Mass of the first particle, m1=1kg
- Velocity of the first particle, v1=2m/s
- Mass of the second particle, m2=0.5kg
- Velocity of the second particle, v2=6m/s
2. Substitute the values into the formula:
Vcm=(1kg⋅2m/s)+(0.5kg⋅6m/s)1kg+0.5kg
3. Calculate the numerator:
- For the first particle: 1⋅2=2kg m/s
- For the second particle: 0.5⋅6=3kg m/s
- Total: 2+3=5kg m/s
4. Calculate the denominator:
1+0.5=1.5kg
5. Calculate the speed of the center of mass:
Vcm=5kg m/s1.5kg=103m/s≈3.33m/s
Final Answer:
The speed of the center of mass of the system is 103m/s or approximately 3.33m/s.
---
- m1 is the mass of the first particle,
- v1 is the speed of the first particle,
- m2 is the mass of the second particle,
- v2 is the speed of the second particle.
- Mass of the first particle, m1=1kg
- Velocity of the first particle, v1=2m/s
- Mass of the second particle, m2=0.5kg
- Velocity of the second particle, v2=6m/s
Vcm=(1kg⋅2m/s)+(0.5kg⋅6m/s)1kg+0.5kg
- For the first particle: 1⋅2=2kg m/s
- For the second particle: 0.5⋅6=3kg m/s
- Total: 2+3=5kg m/s
1+0.5=1.5kg
Vcm=5kg m/s1.5kg=103m/s≈3.33m/s
The speed of the center of mass of the system is 103m/s or approximately 3.33m/s.
Topper's Solved these Questions
Similar Questions
Two particle of mass 2kgand1kg are moving along the same straight line with speeds 2m/sand5m/s respectively. What is the speed of the centre of mass of the system if both the particles are moving (a) in same direction (b) in opposite direction ?
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View Solution
Knowledge Check
Two particles of masses 2 kg and 4 kg are approaching each other with acceleration 1ms−2 and 2ms−2, respectively, on a smooth horizontal surface. Find the magnitude of acceleration of center of mass of the system.
A1B2C3D4Two bodies of masses 1kgand2kg are moving in two perpendicular direction with velocities 1m/sand2m/s as shown in figure. The velocity of the centre of mass (in magnitide) of the system will be :
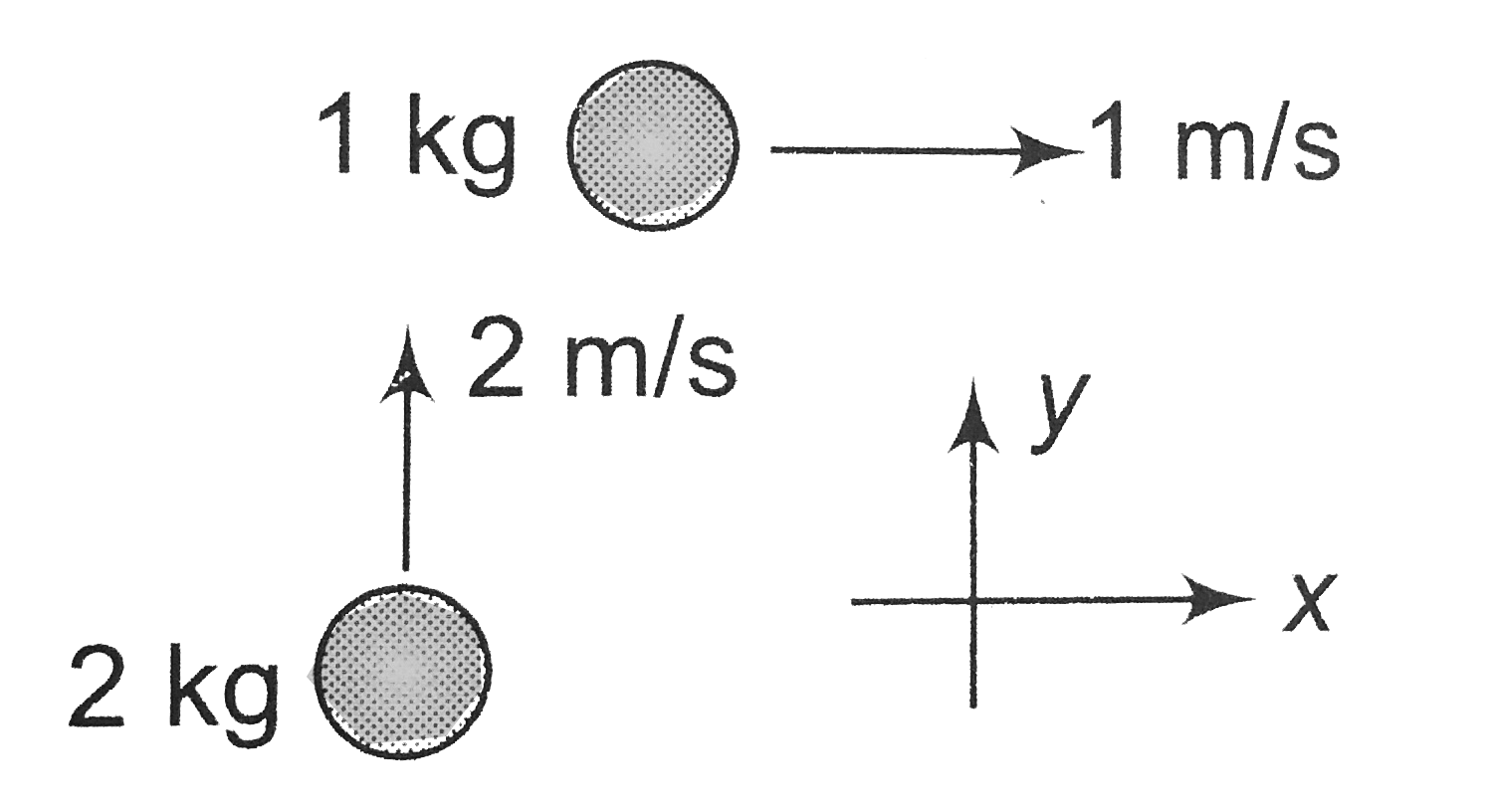 A3m/sB1.67m/sC1.5m/sD1.37m/s
A3m/sB1.67m/sC1.5m/sD1.37m/sThree bodies having masses 5 kg, 4 kg and 2 kg is moving at the speed of 5 m/sand2m//s respectively along X-axis.The magnitude of velocity of centre of mass is
A1.0m/sB4m/sC0.9m/sD1.3m/s
Two particles having masses of 2 kg and 3 kg are moving along the same straight line with velocities of 3ms−1and6ms−1 respectively. Calculate the speed of centre of mass of system if particles are moving in
(a) same direction. (b) in opposite direction.
View SolutionTwo bodies of masses 2 kg and 1 kg are moving along the same line with speeds 2ms−1 and 5ms−1 respectively. What is the speed of the centre of mass of the system if the two bodies are moving (i) in same direction and (ii) in opposite directions?
View SolutionTwo particles of masses 2kg and 4kg are approaching towards each other with accelerations 1m/s2 and 2m/s2, respectively, on a smooth horizontal surface. Then find the acceleration of centre of mass of the system and direction of acceleration of CM.
View SolutionTwo bodies of masses 2 kg and 4 kg are moving with velocities 2 m/s and 10 m/s respectively along same direction. Then the velocity of their centre of mass will be
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then

View Solution
