A hole of radius R/2 is cut from a thin circular plate of raduis R as shown in the figure. If the mass of the remaining plate is M, then find moment of inertia of the plate about an axis through O perpendicular to plane

1325MR2
1324MR2
1124MR2
1125MR2
The correct Answer is:B
Let the mass of disc without hole =m
The mass of cut out hole of radius R2 is m4
∴m−m4=M or m=43M
Moment of inertia of given body about axis passing through O
=MI of complete disc -MI of cut out hole .
=12(4M3)R2−[12(M3)(R2)2+M3(R2)2]=1324MR2
Topper's Solved these Questions
Similar Questions
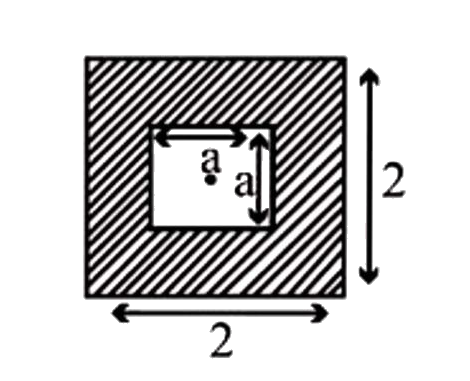
A square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
View SolutionA circular hole of radius r/2 is cut from a circular disc of radius 'r'. The disc lies in the xy plane. Determine the moment of inertia about an axis passing through the centre and perpendicular to the plane of the disc.
View Solution
Knowledge Check
An isosceles triangular piece is cut a square plate of side l. The piece is one-fourth of the square and mass of the remaining plate is M. The moment of inertia of the plate about an axis passing through O and perpendicular to its plane is
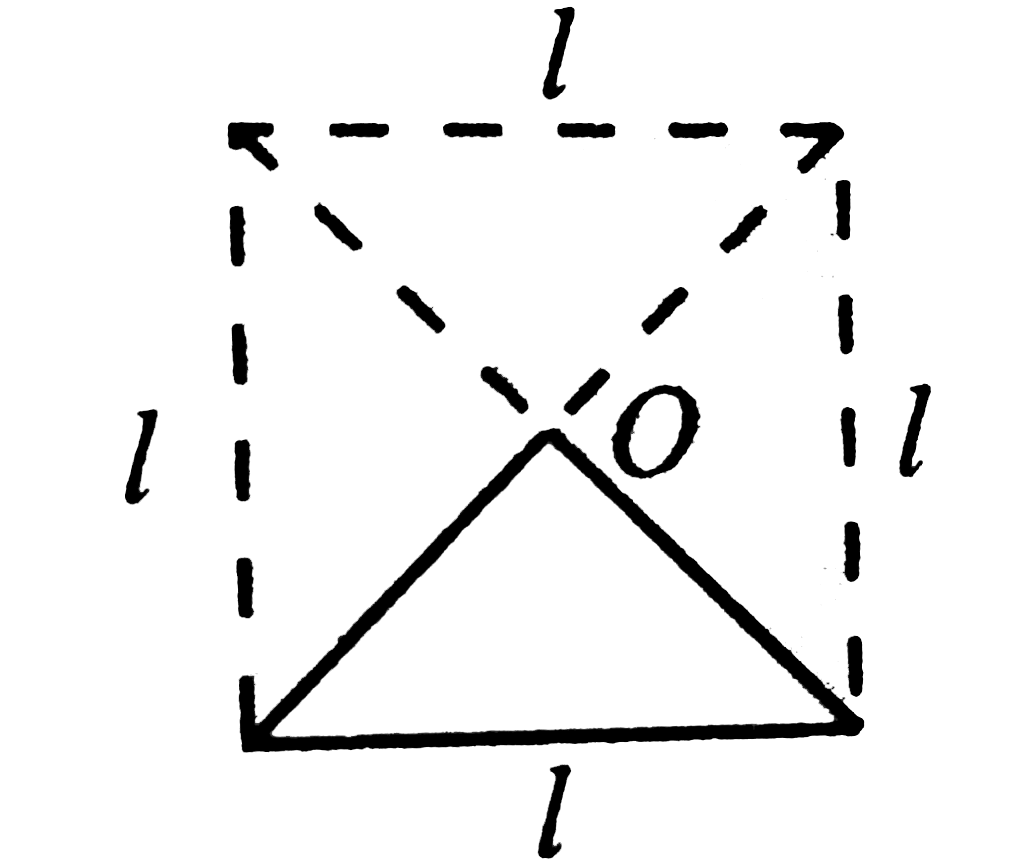 AMl26BMl212CMl224DMl23
AMl26BMl212CMl224DMl23A square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :
 A964Ma2B316Ma2C512Ma2DMa26
A964Ma2B316Ma2C512Ma2DMa26A concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
A1324MR2B1124MR2C1332MR2D1532MR2
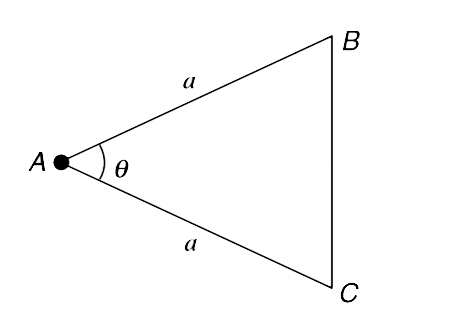
The triangular plate described in the last question has angle <A=θ. Now find its moment of inertia about an axis through A perpendicular to the plane of the plate.
View SolutionA hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionIf I moment of inertia of a thin circular plate about an axis passing through tangent of plate in its plane. The moment of inertia of same circular plate about an axis perpendicular to its plane and passing through its centre is
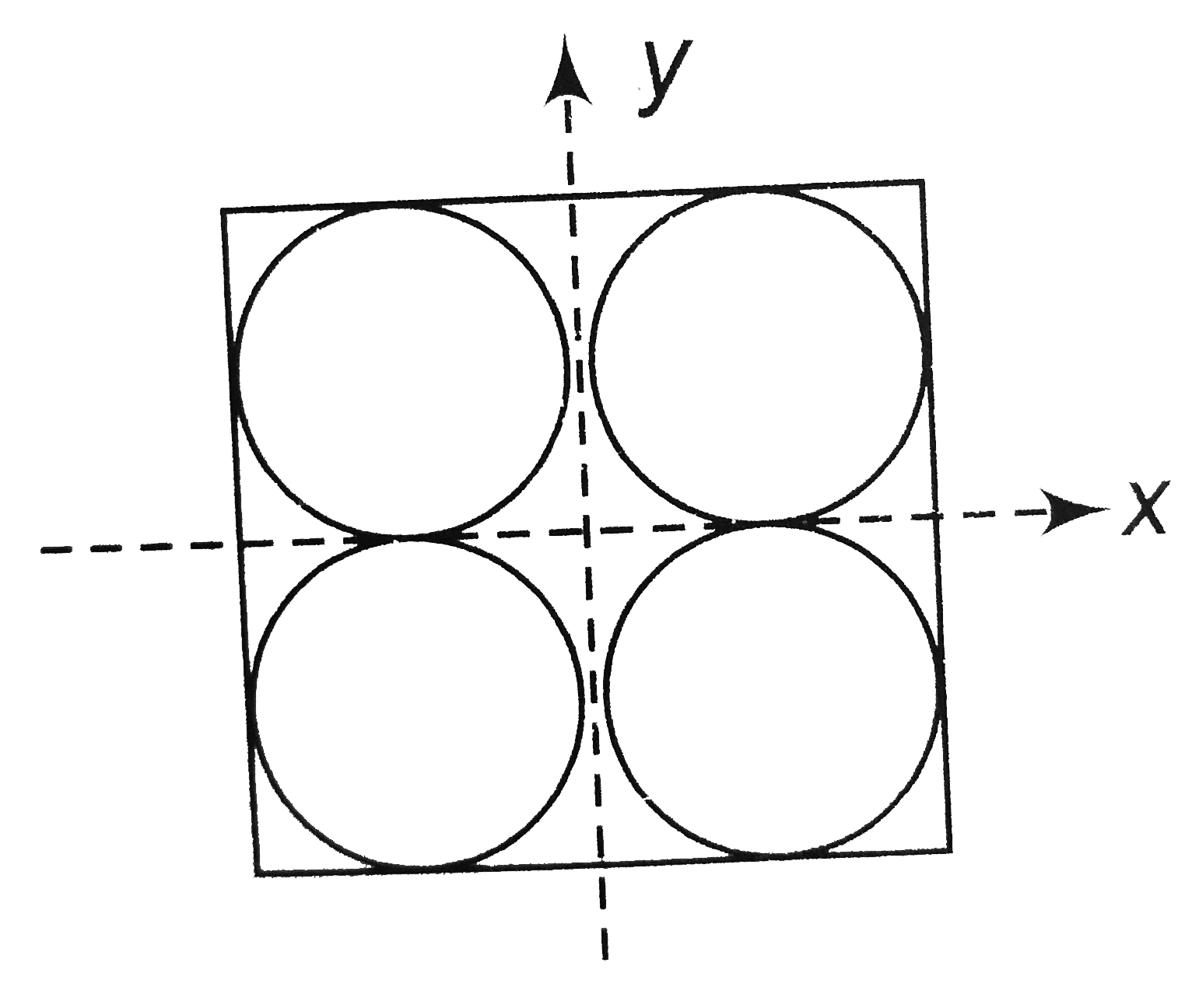
View SolutionFour holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is :
 .
.
View Solution
