Consider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
K1=K2
K1S1=K2S2
K1A1S1=K2A2S2
K1A1=K2A2
The correct Answer is:D
Thermal resistance should be equal, to lK1A1=lK2A2⇒K1A1=K2A2
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Exercise-31videos
HEAT TRANSFER
- BOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Advancel Level Problems17videos
HEAT TRANSFER
- BOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Exercise-21videos
HEAT TRANSFER
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - Exercise21videos
GRAVITATION
- BOOK - RESONANCECHAPTER - KINEMATICSEXERCISE - Exercise65videos
KINEMATICS
Similar Questions
Two metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View Solution
Knowledge Check
- Question 1 - Select One
Condider two rods of same length and different specific heats (s1,s2), thermal conductivities (K1,K2) and areas of cross-section (A1,A2) and both having temperatures (T1,T2) at their ends. If their rate of loss of heat due to conduction are equal, then
AK1A1=K2A2BK1A1s1=K2A2s2CK2A1=K1A2DK2A1s2=K1A2s1 - Question 2 - Select One
Two rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oil - Question 3 - Select One
All the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
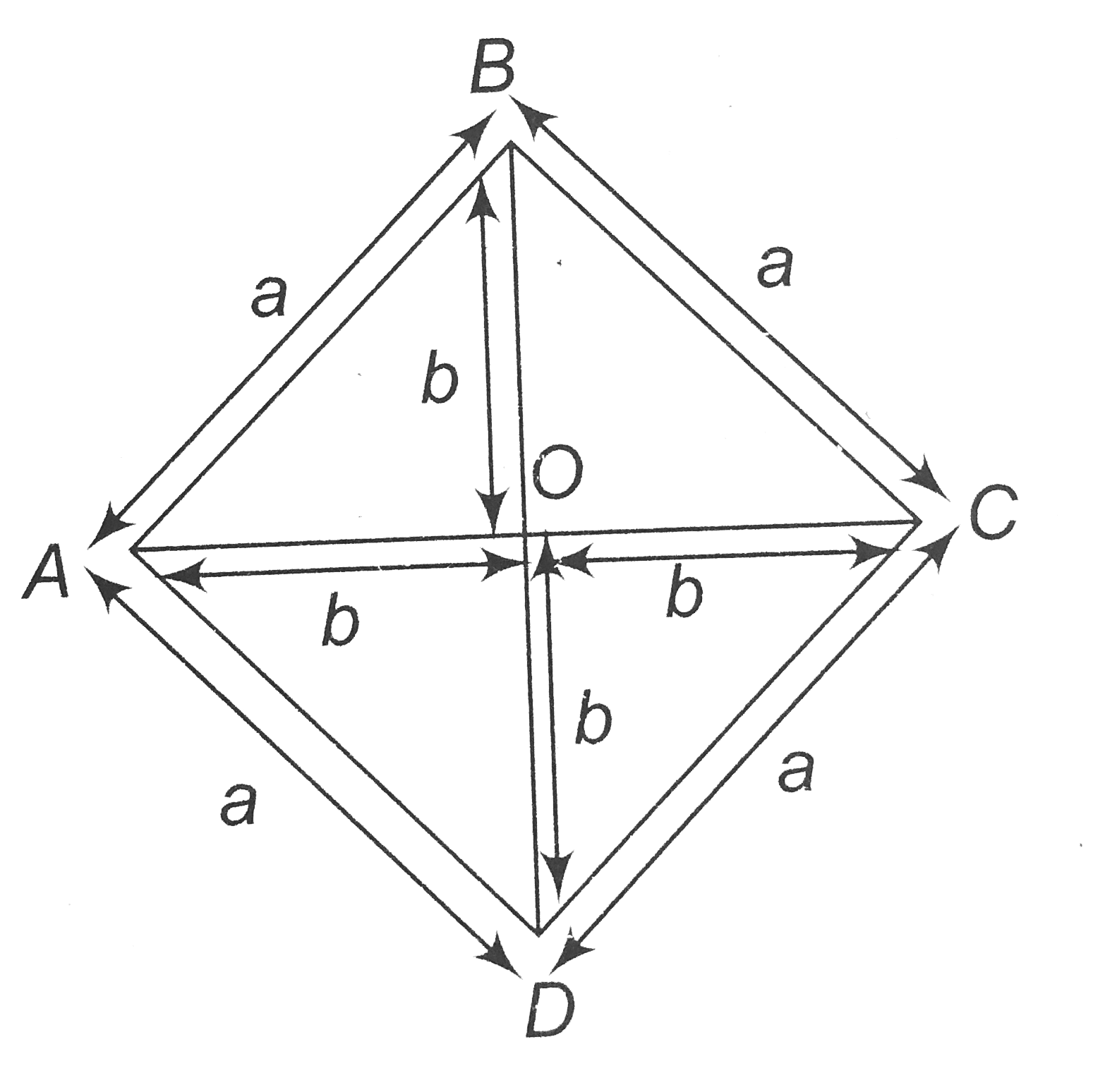 ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
A cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T1 and the other end in surrounding at temperature T2. Surface of the rod exposed to the surrounding has emissivity e. Also T2=Ts+ΔTandTs>>ΔT. If T1−Ts∝ΔT,find the proportionality constant.
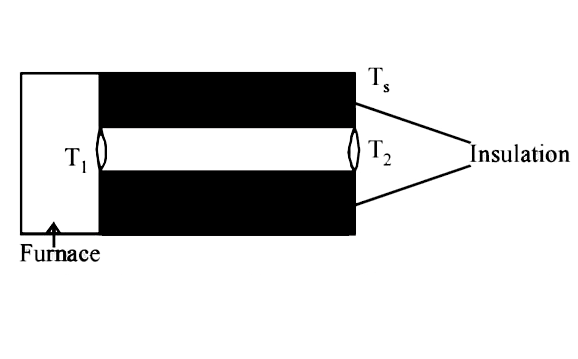 View Solution
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionActivation energy (Ea) and rate constants (k1andk2) of a chemical reaction at two different temperature (T1andT2) are related by
View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View Solution

