A simple pendulum long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration . The period of small oscillations of the pendulum about its equilibrium position is ltbRgt 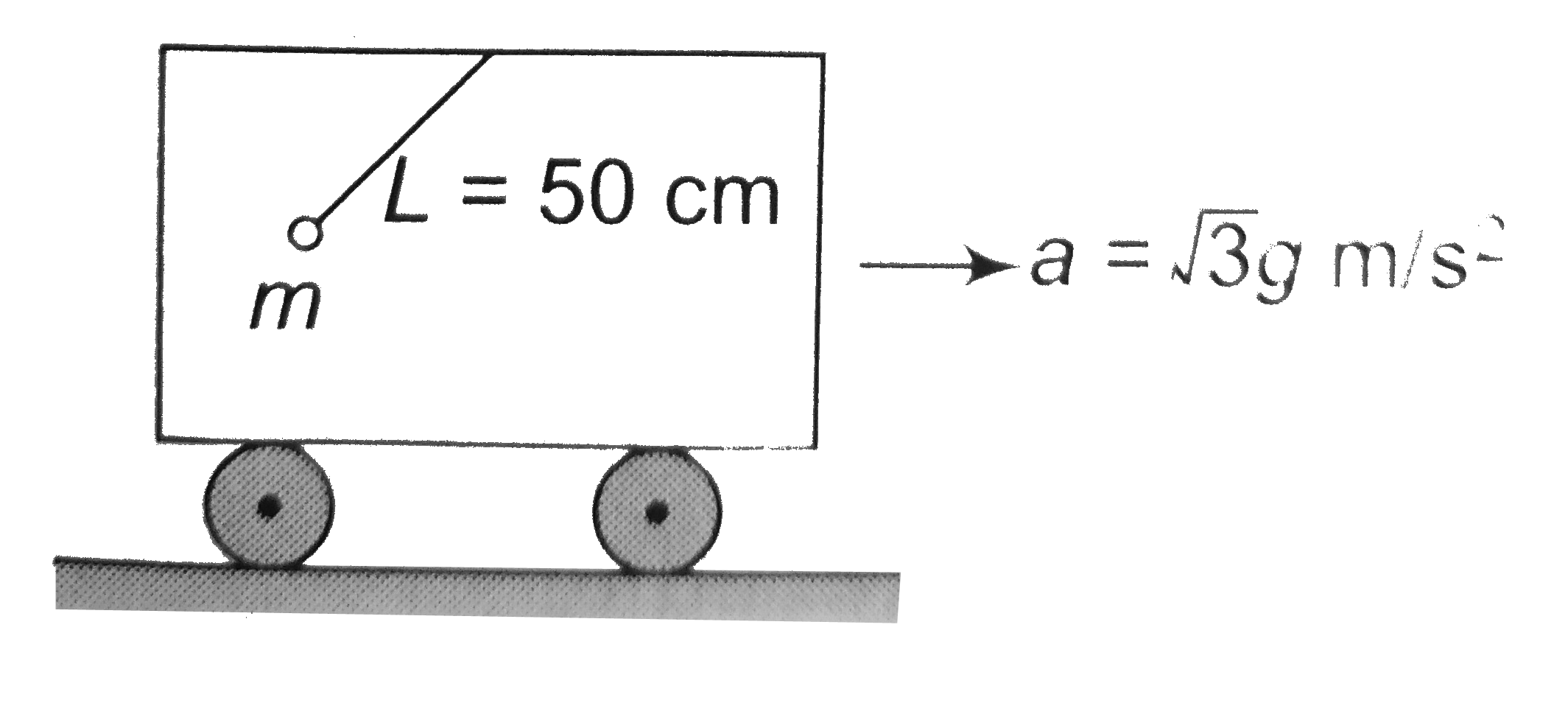
1.0 sec
1.53 sec
1.68 sec
The correct Answer is:A
With respect to the cart, equilibrium position of the pendulum is shown.
If displaced by small angle from this positon, then it will execute SHM about this equilibrium position, time period of which is given by
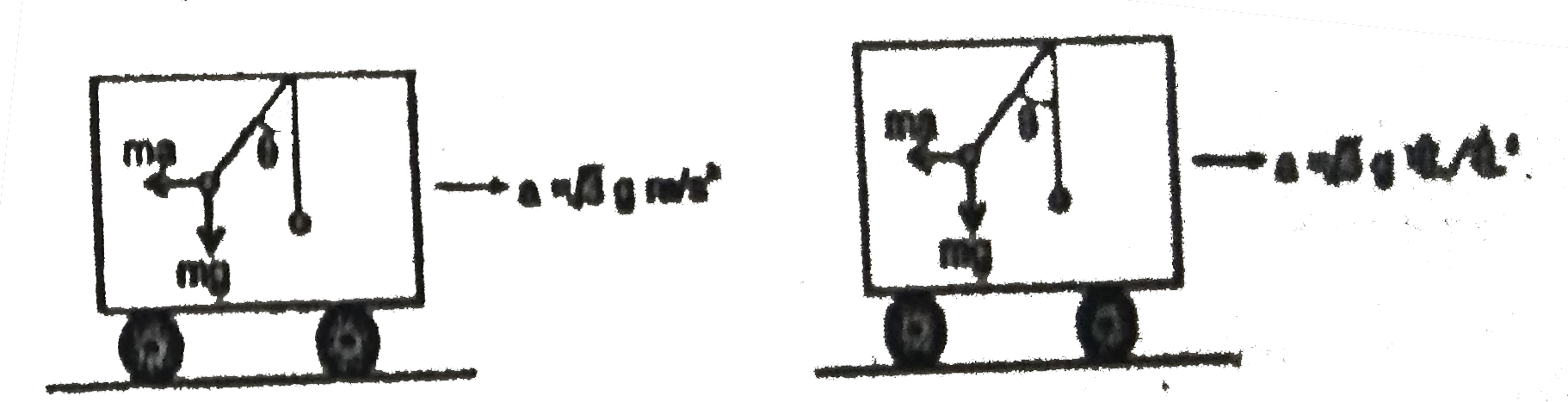
second
Topper's Solved these Questions
Similar Questions
A simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionA 60cm pendulum is fixed in an aeroplane taking off at an angle α=30∘ to the horizontal with an acceleration a=4.0ms−2. Determine the period of oscillation of the pendulum.
View Solution
Knowledge Check
- Question 1 - Select One or More
A simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of sin−1(ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2 - Question 2 - Select One
A simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
AT=2π√lgBT=2π√lg+aCT=2π√l(g2+a2)DT=2π√lg−a - Question 3 - Select One or More
A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of tan−1(1−ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2
A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
View SolutionA simple pendulum is suspended from the roof of a train. If the train is moving with an acceleration 49cm/s2. Then the angle of inclination of the string about the vertical will be
View SolutionA simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration α, then the time period is given by T=2π√(IT) where g is equal to
View SolutionA seconds pendulum is suspended form the roof of a lift. If the lift is moving up with an acceleration 9.8m/s2, its time period is
View SolutionThe path length of oscillation of simple pendulum of length 1 m is 16 cm. Its maximum velocity is (take, g=π2m/s2)
View Solution

