Two particles of charge $q_{1}$ and $q_{2}$ are separated by distance $d$ as shown in figure. Chrage $q_{1}$ is situarted at the origin. The net electirc field due to the particles is zero at $x = d / 4$ . With $V = 0$ at infinity, the location of a point in terms of $d$ on the $x$ axis (other at infinfity) at which the elctrical potential due to the two particles is zero, is given by:

A

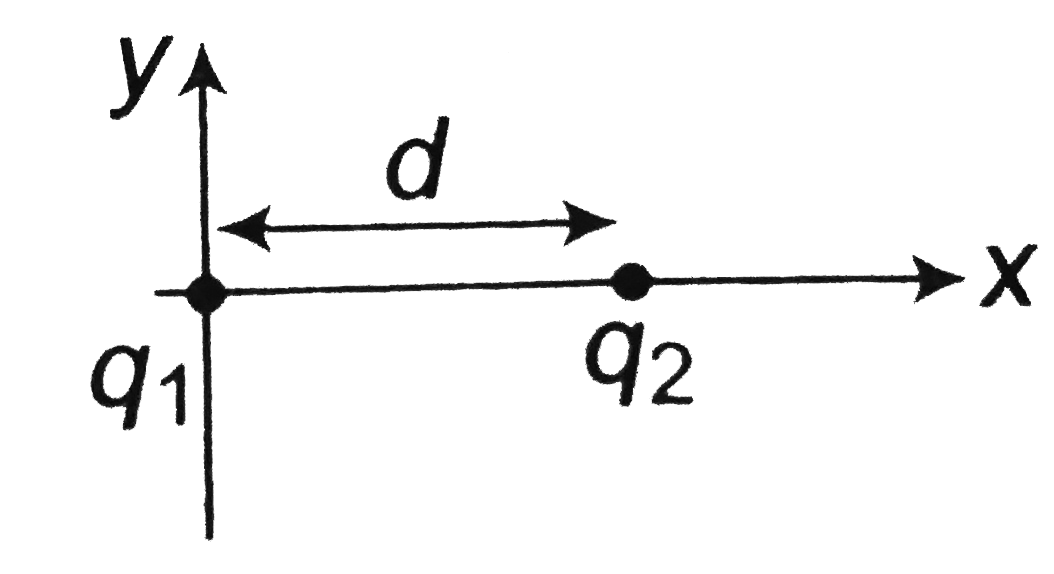
d/4

B

16d

C

$- 16 d$

D

no point on the axis

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$\to E$ is zero in between the two charges. So both charges must have the same sign.
Therefore, electric potential cannot be zero anywhere on the axis.

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Two point charges Q and $- Q / 4$ are separated by a distance $X$ . Then .
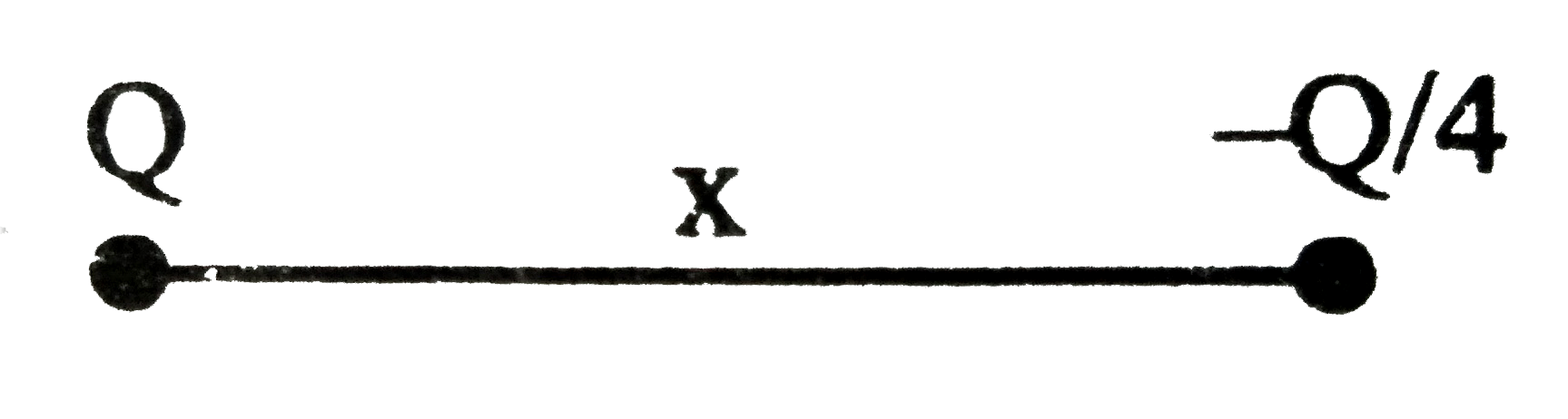Apotential is zero at a point on the axis which is $x / 3$ on the right side of the cahrge $- q / 4$
Bpotential is zero at a point on the axis which is $x / 5$ on the left side fo the charge $- Q / 4$
Celectric field is zero at a point on the axis which is at a distance $x$ on the right side fo the charge $- Q / 4$
Dthere exist two points on the axis where electric field is zero.
Question 2 - Select One
Two charge $Q_{1} = 18 μ C$ and $Q_{2} = - 2 μ C$ are separted by a distance R, and $Q_{1}$ is on the left off $Q_{2}$ . The distance of the point where the net electric field is zero is
Abetween $Q_{1}$ and $Q_{2}$
Bleft of $Q_{1} a t R / 2$
Cright of $Q_{2}$ at R
Dright of $Q_{2}$ at $R / 2$
Question 3 - Select One
two point charges + 16 q and -4q located at x=0 and x=L respectively. the location of a point on the x-axis from x=0, at which the net electric field due to these two charges is zero is
AL
B2L
C $\frac{L}{2}$
D $\frac{L}{4}$

RESONANCE-PART TEST 5-Exercise

Home
Ask Doubt
Profile