Figure shows a plot of potential energy function U(x)=kx2 where x=displacement and k=constant. Identify the correct conservative force function F(x)





The correct Answer is:A
F=−dUdx
∵U(x)=kx2
f=−2kx

Topper's Solved these Questions
Similar Questions
Figure (A) shows potential energy as a function of x for a particle that is moving in the x-direction under a coriservative force.
Figure (B) shows potential energy as a function of x for another particle that is moving in the x-direction under a conservative force.
Figure (C ) shows interaction potential energy as a system of two particles that could move in the x-direction under the mutual conservative force.
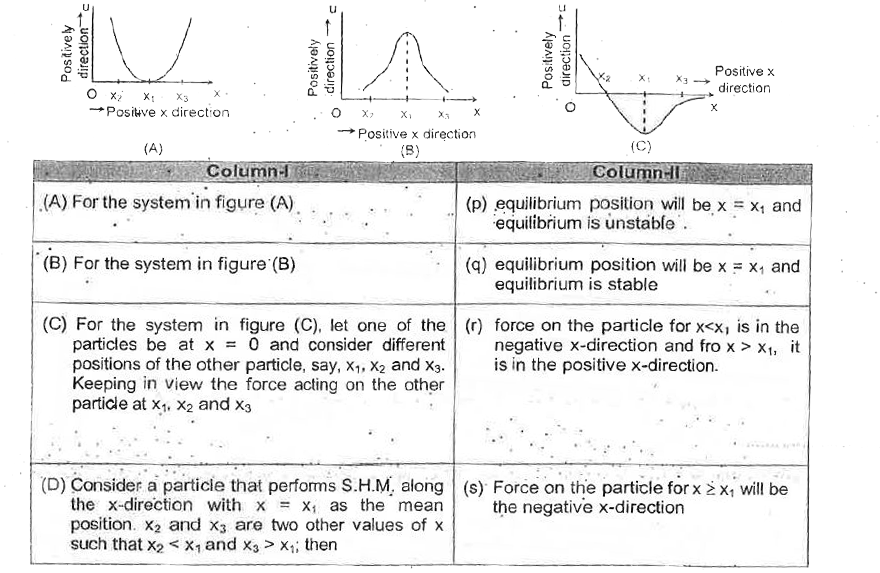
View SolutionCheck the points where the constant function f(x)=kis continuous.
View Solution
Knowledge Check
Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose tha Emech=8 J, the incorrect statement for this system is :
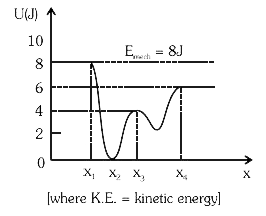 Aat x>x4, K.E. is constant throughout the region.Bat x<x1 K.E. is smallest and the particle is moving at the slowest speed.Cat x=x2 , K.E is greatest and the particle is moving at the fastest speed.Dat x=x3, K.E. = 4 J
Aat x>x4, K.E. is constant throughout the region.Bat x<x1 K.E. is smallest and the particle is moving at the slowest speed.Cat x=x2 , K.E is greatest and the particle is moving at the fastest speed.Dat x=x3, K.E. = 4 JFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
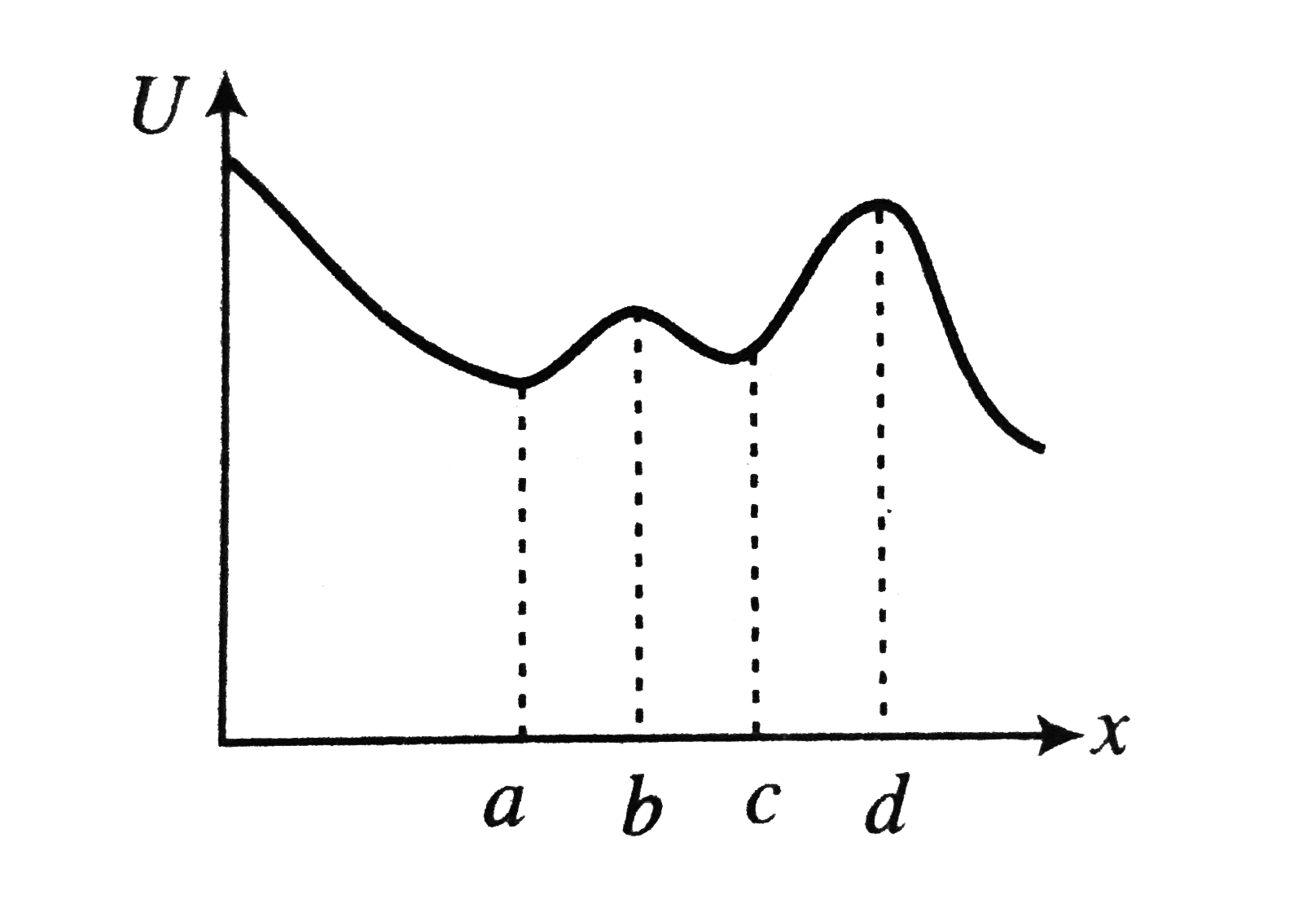 Aa, c, and d are points of equilibriumBa is a point of stable equilibriumCb is a unstable equilibrium pointDAll of the above
Aa, c, and d are points of equilibriumBa is a point of stable equilibriumCb is a unstable equilibrium pointDAll of the aboveThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
A−3kB+3kCkDNone of these
A particle is moving on frictionless XY-plane. It is acted on by a conservative force described by the potential-energy function.
U(x,y,z)=12k(x2+y2+z2)
where , k=constant
Derive an expression for the force an the particle.
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
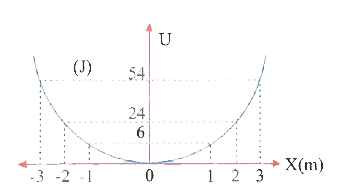
View SolutionA particle located in one dimensional potential field has potential energy functionU(x)=ax2−bx3, where a and b are positive constants. The position of equilibrium corresponds to x equal to
View SolutionThe potential energy U for a force field →F is such that U=−kxy where K is a constant . Then
View SolutionA particle located in a one-dimensional potential field has its potential energy function as U(x)=ax4−bx2, where a and b are positive constants. The position of equilibrium x corresponds to
View Solution
