A 1000m long rod of density 10.0×104kg/m3 and having young's modulus Y=1011Pa, is clamped at one end. It is hammered at the other free end as shown in the figure. The logitudinal pulse goes to right end, gets reflected and again returns to the left end. How much time (in sec) the pulse take to go back to initial point ?
_S01_029_Q01.png) .
.
The correct Answer is:2
Velocity of longitudinal u=√Yρ=√101110×104=103ms−1
Required time 2lv=2×1000103=2s.
Topper's Solved these Questions
Similar Questions
A string that is 10 cm long is fixed at both ends. At t=0, a pulse travelling from left to right at 1cm/sis4.0cm from the right end as shown in figure. Determine the next two times when the pulse will be at that point again. State in each case whether the pulse is upright or inverted .
 .
.
View SolutionA 100 g wire is held under a tension of 220 N with one end at x=0 and the other x=10.0m. At time t=0 pulse 2 is sent along the wire from the end at x=0. What position x do the pulses begin to meet?
View Solution
Knowledge Check
A 100−m long rod of density 10.0×104kg/m3 and having Young's modulus Y=1011Pa, is clamped at one end . It is hammered at the other free end. The longitudinal pulse goes to right end , gets reflected and again returns to the left end . How much time the pulse take to go back to initial point.
 A0.1sB0.2sC0.3sD2s
A0.1sB0.2sC0.3sD2sA string of length 0.4 m and mass 10−2 kg is clamped at its ends. The tension in the string is 1.6 N. When a pulse travels along the string the shape of the string is found to be the same at times t and t+△t. The value △t is
A0.05sB0.1sC0.2sD0.4sA string of length 0.4m and mass 10−2kg is clamped at one end . The tension in the string is 1.6N. The identical wave pulses are generated at the free end after regular interval of time , Δt . The minimum value of Δt , so that a constructive interference takes place between successive pulses is
A0.1sB0.05sC0.2sDconstructive interference cannot take place
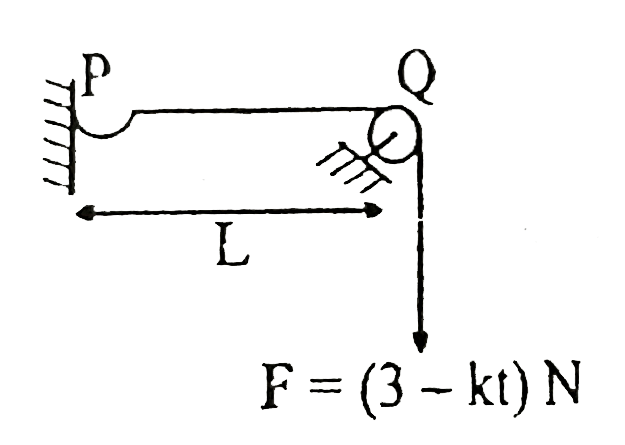
In the given figure a string of linear mass density 3×10−2 kg//m and length L=1 m, is stretched by a froce F=(3−kt)N, where k is a constant and t is time in sec. At the time t=0, a pulse is generated at the end P of the string Find the value of k (in N//s) if the value of force becomes zero as the pulse reaches point Q.
View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1-0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA rod of length 1.0m and mass 0.5kg fixed at ond is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required?
View SolutionA ball of mass 10−2kg and having charge +3×10−6C is tied at one end of a 1m along thread. The other end of the thread is fixed and a charge −3×10−6C is placed at this end. The ball can move in the circulr orbit of radius 1m in the vertical plane. Initially, the ball is at the bottom. Find the monimum initial horizontal velocity of the ball, so that it will be able to complete the full circle.
View SolutionTwo men are standing on opposite ends of a bridge 1200 metres long. If they walk towards each other at the rate of 5m/minute and 10m/minute respectively in how much time will they meet each other ?
View Solution
