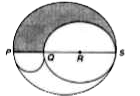
PS is the diameter of a circle of radius 6 cm. The points Q and R cts the diameter Ps. Semi circles are drawn on PQ and Qs as diameters. Find the area of the shaded region.
Area of semicircle(A1)=πr22=π2⋅62
=18πcm2
Area of semicircle(A2)=πr212=2πcm2
Area of semicircle(A3)=πr222=π2⋅16
=8πcm2
Area of shaded region=(A1+A2+A3)
=(18π+2π−8π)
=12πcm2.
Similar Questions
PS is the diameter of a circle of radius 6 cm. The points Q and R cts the diameter Ps. Semi circles are drawn on PQ and Qs as diameters. Find the area of the shaded region.
View SolutionPQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal Semicircle are drawn on PQ and QS as diameters. Find the area of the shaded region. Find also the length of boundaries of shaded portion.
View Solution
Knowledge Check
PQRS is the diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semi-circles are drawn with PQ and QS as diameters as shown in the figure alongside. Find the ratio of the area of the shaded region to that of the unshaded region.
 A1:2B25:121C5:18D5:13
A1:2B25:121C5:18D5:13
PQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal Semicircle are drawn on PQ and QS as diameters. Find the area of the shaded region. Find also the length of boundaries of shaded portion.
View SolutionPQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semi-circles are drawn on PQ and QS as diameters as shown in figure. Find the perimeter of the shaded region.
View SolutionCircle inside a Circle : PQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal. Semi circles are drawn on PQ and QS as diameters, as shown in Figure. Find the perimeter and area of shaded Region.
View SolutionCircle inside a Circle : PQRS is a diameter of a circle of radius 6 cm. The length PQ;QR and RS are equal. Semi circles are drawn on PQ and QS as diameters as shown in Figure. Find the perimeter and area of shaded Region.
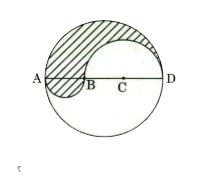
View SolutionABCD is a diameter of a circle of radius 6 cm such that AB = BC = CD. Semicircles are drawn on AB and BD as diameters, as shown in the given figure. Find the area of the shaded region.

View SolutionIn the figure given below, ABCD is the diameter of a circle of radius 9 cm. The lengths AB, BC and CD are equal. Semicircles are drawn on AB and BD as diameters as shown in the figure. What is the area of the shaded region ?
View SolutionPQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semi-circles are drawn on PQ and QS as diameters as shown in Fig.17. Find the perimeter of the shaded region.
View Solution
