Circle inside a Circle : PQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal. Semi circles are drawn on PQ and QS as diameters, as shown in Figure. Find the perimeter and area of shaded Region.
To solve the problem, we will follow these steps:
Step 1: Understand the Circle and its Diameter
Given that PQRS is a diameter of a circle with a radius of 6 cm, we can determine the diameter of the circle.
Hint: Remember that the diameter is twice the radius.
Solution:
Diameter (PS) = 2 × Radius = 2 × 6 cm = 12 cm.
Step 2: Determine the Lengths of PQ, QR, and RS
Since the lengths PQ, QR, and RS are equal, we can find the length of each segment.
Hint: If the total length is divided into equal parts, divide the total length by the number of parts.
Solution:
Length of each segment (PQ, QR, RS) = Total Diameter / 3 = 12 cm / 3 = 4 cm.
Step 3: Calculate the Length of QS
Now, we can find the length of QS, which is the sum of QR and RS.
Hint: Add the lengths of QR and RS together.
Solution:
Length of QS = QR + RS = 4 cm + 4 cm = 8 cm.
Step 4: Calculate the Perimeter of the Shaded Region
The perimeter consists of the arcs of the semicircles drawn on PQ and QS. We will calculate the perimeter using the formula for the arc length of a semicircle.
Hint: The perimeter of a semicircle is given by the formula πr.
Solution:
1. Arc of semicircle with diameter PS (radius = 6 cm):
Perimeter=π×6
2. Arc of semicircle with diameter PQ (radius = 2 cm):
Perimeter=π×2
3. Arc of semicircle with diameter QS (radius = 4 cm):
Perimeter=π×4
Total Perimeter = π×6+π×2+π×4=π(6+2+4)=12π.
Using π≈227:
Total Perimeter = 12×227=2647≈37.71 cm.
Step 5: Calculate the Area of the Shaded Region
The area of the shaded region can be found by subtracting the area of the semicircle with QS as the diameter from the sum of the areas of the semicircles with PS and PQ as diameters.
Hint: The area of a semicircle is given by the formula 12πr2.
Solution:
1. Area of semicircle with diameter PS (radius = 6 cm):
Area=12π(62)=12π(36)=18π
2. Area of semicircle with diameter PQ (radius = 2 cm):
Area=12π(22)=12π(4)=2π
3. Area of semicircle with diameter QS (radius = 4 cm):
Area=12π(42)=12π(16)=8π
Total Area = Area of PS + Area of PQ - Area of QS:
=18π+2π−8π=12π
Using π≈227:
Total Area = 12×227=2647≈37.71 cm².
Final Answers:
- Perimeter of the shaded region = 37.71 cm
- Area of the shaded region = 37.71 cm²
Given that PQRS is a diameter of a circle with a radius of 6 cm, we can determine the diameter of the circle.
Diameter (PS) = 2 × Radius = 2 × 6 cm = 12 cm.
Since the lengths PQ, QR, and RS are equal, we can find the length of each segment.
Length of each segment (PQ, QR, RS) = Total Diameter / 3 = 12 cm / 3 = 4 cm.
Now, we can find the length of QS, which is the sum of QR and RS.
Length of QS = QR + RS = 4 cm + 4 cm = 8 cm.
The perimeter consists of the arcs of the semicircles drawn on PQ and QS. We will calculate the perimeter using the formula for the arc length of a semicircle.
1. Arc of semicircle with diameter PS (radius = 6 cm):
Perimeter=π×6
2. Arc of semicircle with diameter PQ (radius = 2 cm):
Perimeter=π×2
Perimeter=π×4
Total Perimeter = 12×227=2647≈37.71 cm.
The area of the shaded region can be found by subtracting the area of the semicircle with QS as the diameter from the sum of the areas of the semicircles with PS and PQ as diameters.
1. Area of semicircle with diameter PS (radius = 6 cm):
Area=12π(62)=12π(36)=18π
Area=12π(22)=12π(4)=2π
Area=12π(42)=12π(16)=8π
=18π+2π−8π=12π
Total Area = 12×227=2647≈37.71 cm².
- Perimeter of the shaded region = 37.71 cm
- Area of the shaded region = 37.71 cm²
Topper's Solved these Questions
Similar Questions
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semi-circles are drawn on PQ and QS as diameters as shown in Fig.17. Find the perimeter of the shaded region.
View SolutionPQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal Semicircle are drawn on PQ and QS as diameters. Find the area of the shaded region. Find also the length of boundaries of shaded portion.
View Solution
Knowledge Check
What will be 4 times the diameter of a circle . If the radius of the circle is 2cm?
A12cmB14cmC16cmD18cm
The diameter of a circle is 28 cm. Find its :
area
View SolutionFind the area of a circle of diameter 7 cm.
View SolutionThe diameter of a circle is 9 cm, find its radius.
View SolutionThe diameter of a circle is 14 cm, find its radius.
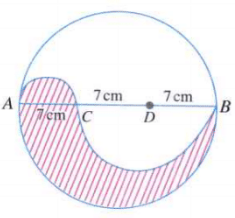
View SolutionGiven is a circle with AB as a diameter of 21 cm. Points C and D lie on the diameter such that AC=7cm,CD=DB=7cm. Semicircles are drawn on the diameter as shown. Find the area of the shaded region.
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
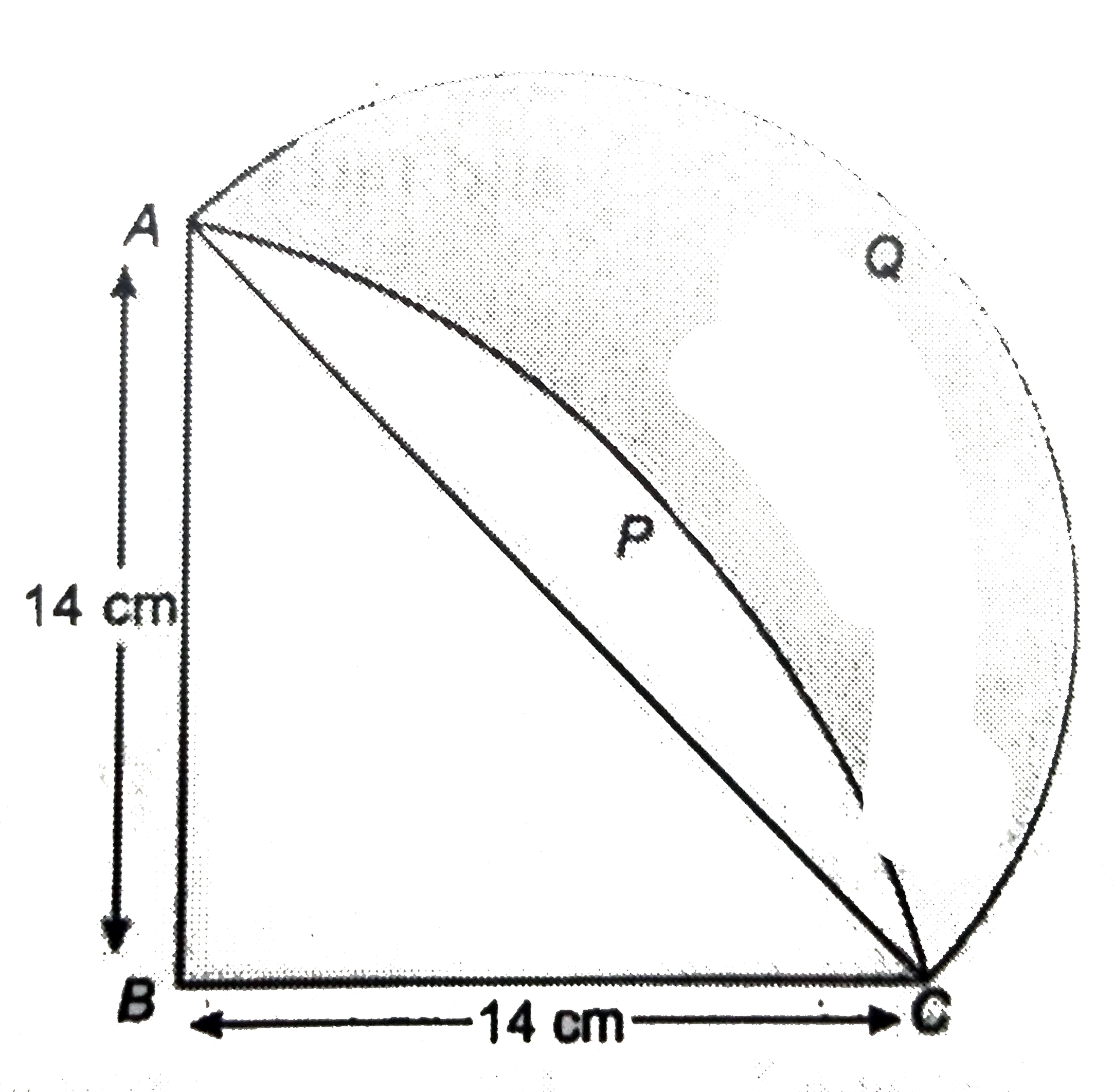
View Solution
