An ideal gas expands from V to $2 V$ in 4 separate processes. Where process 1 is isothermal process 2 is adiabatic, process 3 is free expansion and process 4 is isobaric. If $E_{1}, E_{2}, E_{3}$ and $E_{4}$ are the changes in average kinetic energy of the molecules in the isothermal, adiabatic free expansion and isobaric process respectively then choose the correct options.

A

$E_{2} = E_{3}$

B

$E_{1} = E_{3}$

C

$E_{1} > E_{4}$

D

$E_{4} > E_{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, D

Ave $K e \propto$ temperature.
In isothermal and free expansion there is no temperature change hence $E_{1} = E_{3}$ . In isobaric expansion process, the temperature of gas increases hence average KE of molecules increases.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A gas is expanded from volume $V_{0}$ to $2 V_{0}$ under three different processes, as shown in the figure. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let $Δ U_{1}, Δ U_{2}$ and $Δ U_{3}$ be the change in internal energy of the gas in these three processes. Then

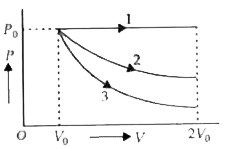A $Δ U_{1} > Δ U_{2} > Δ U_{3}$
B $Δ U_{1} < Δ U_{2} < Δ U_{3}$
C $Δ U_{2} < Δ U_{1} < Δ U_{3}$
D $Δ U_{2} < Δ U_{3} < Δ U_{1}$
Question 2 - Select One
A gas is expanded form volume $V_{0} \to 2 V_{0}$ under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let $Δ U_{1}, Δ U_{2} and Δ U_{3}$ be the change in internal energy of the gs in these three processes then

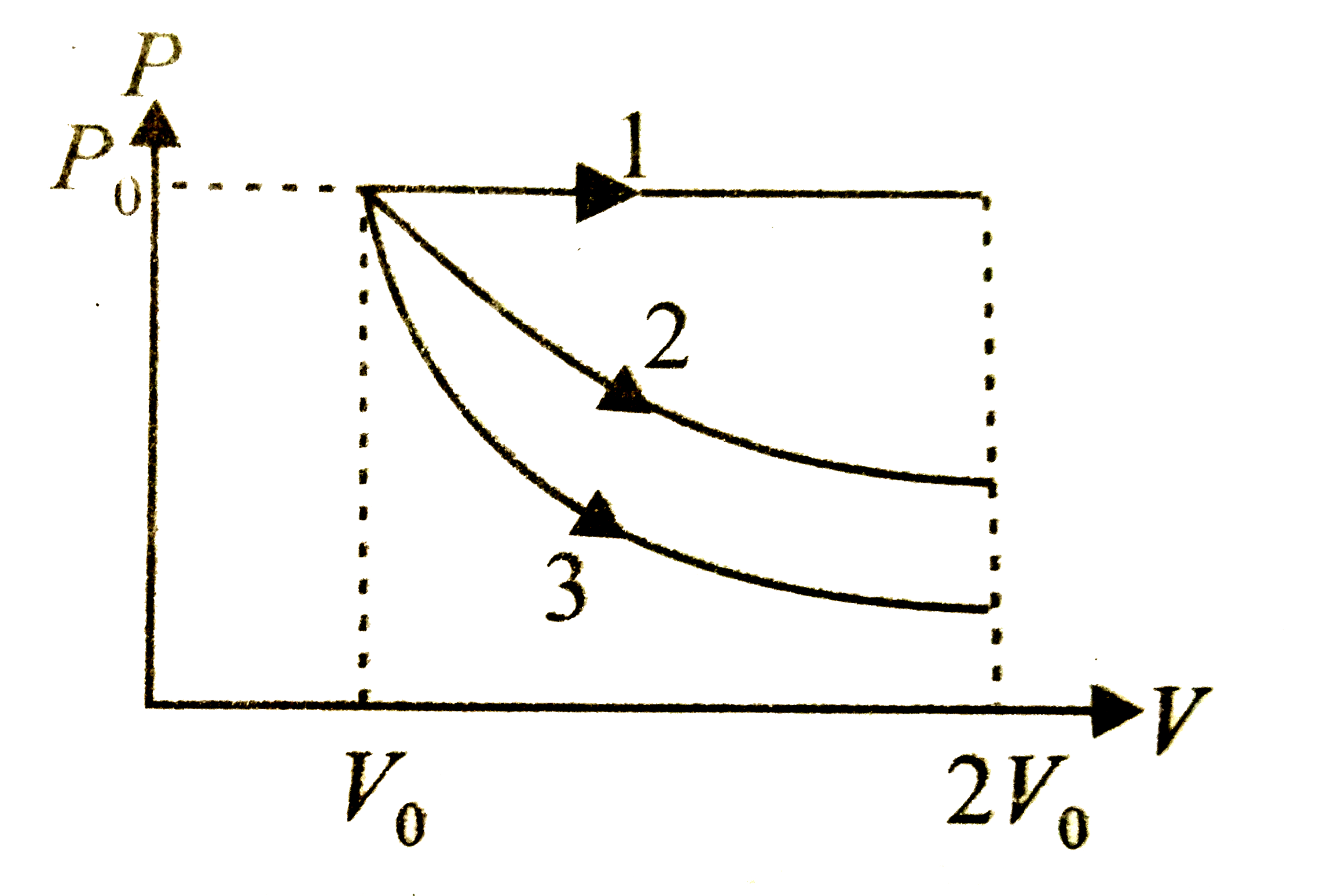A $Δ U_{1} > Δ U_{2} > Δ U_{3}$
B $Δ U_{1} < Δ U_{2} < Δ U_{3}$
C $Δ U_{1} < Δ U_{2} < Δ U_{3}$
D $Δ U_{1} < Δ U_{2} < Δ U_{3}$
Question 3 - Select One
Suppose that the voulme of a certain ideal gas is to be doubled by one the following processes :
(1) isothermal expansion
(2) adiabatic expansion
(3) free expansion in isulated condition
(4) expansion at constant pressure .
If $E_{1}, E_{2}, E_{3} and E_{4}$ respectively are the changes in average kinetic energy of the molecules for the four processes, them :
A $E_{2} = E_{3}$
B $E_{1} = E_{3}$
C $E_{1} > E_{4}$
D $E_{4} > E_{3}$

RESONANCE-TEST PAPERS-Physics

Home
Ask Doubt
Profile