A box of mass m is initially at rest on a horizontal surface. A constant horizontal force of mg/2 is applied to the box directed to the right. The coefficient of friction of the surface changes with the distance pushed as μ=μ0x where x is the distance fr4om the initial location . For what distance is the box pushed until it comes to rest again?
2μ0
1μ0
12μ0
14μ0
The correct Answer is:B
Net change in kinetic energy =0 ⇒ net work W=0

w=∫dW=∫Fdx−∫μNdx=mg2×0mg10∫x0xdx=0⇒x=1μ0
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 260videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3100videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS45videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
 View Solution
View SolutionA horizontal force of 129.4 N is applied on a 10 kg block which rests on a horizontal surface. If the coefficient of friction is 0.3, the acceleration should be
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
A5NB10NC8NDzero - Question 2 - Select One
A block of mass 5kg is initially at rest on a rough horizontal surface. A force of 45N acts over a distance of 2m. The force of friction acting on the block is 25N. The final kinetic energy of the block is
A40 JB90 JC50 JD140 J - Question 3 - Select One
A block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθ
A 10kg mass is resting on a horizontal surface and horizontal force of 80N is applied. If μ=0.2, the ratio of acceleration without and with friction is (g=10ms−2).
View SolutionA homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
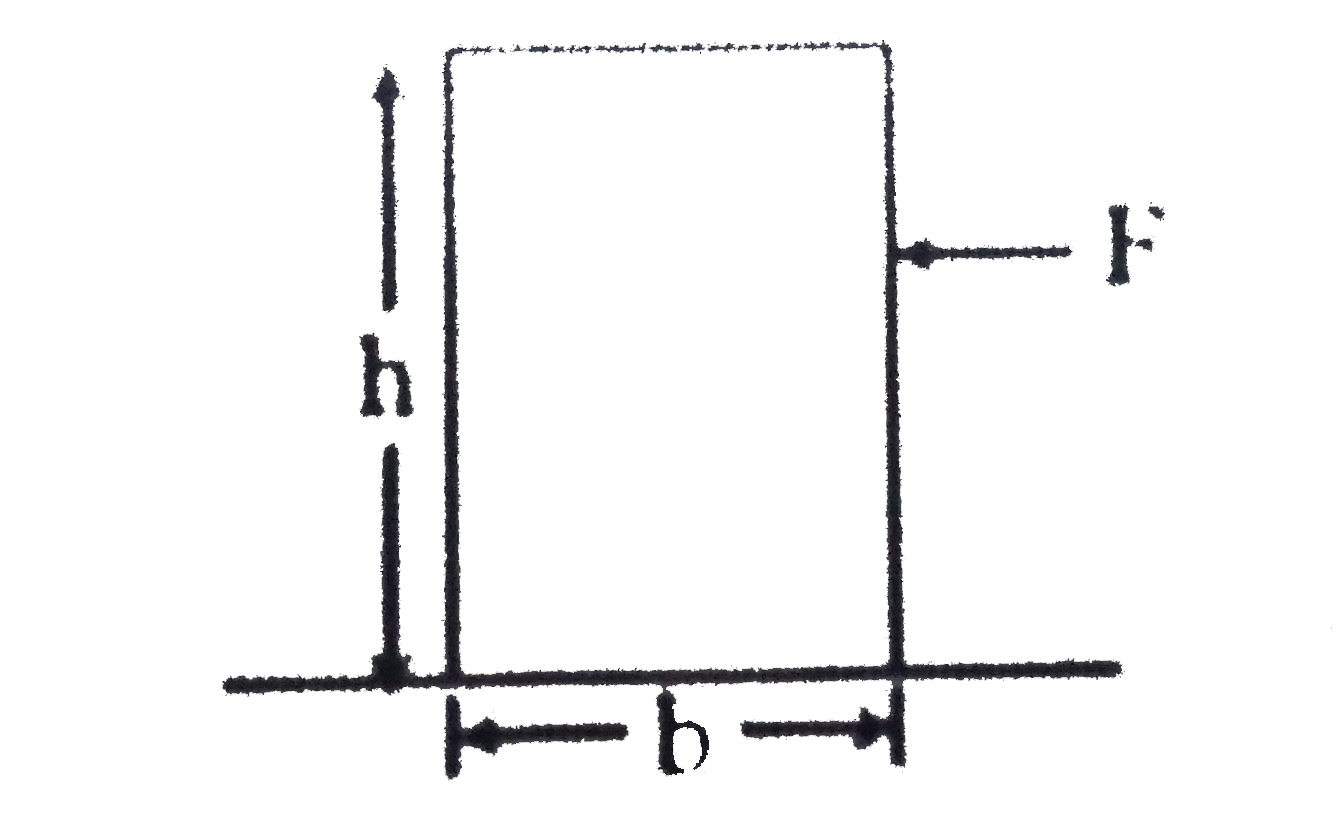 View Solution
View SolutionThe block of mass 'm' initially at x=0 is acted upon by a horizontal force F=a−bx as shown in the figure. The coefficient of friction between the surfaces of contact is μ. The net work done on the block is zero if the block travels a distance of ________ .
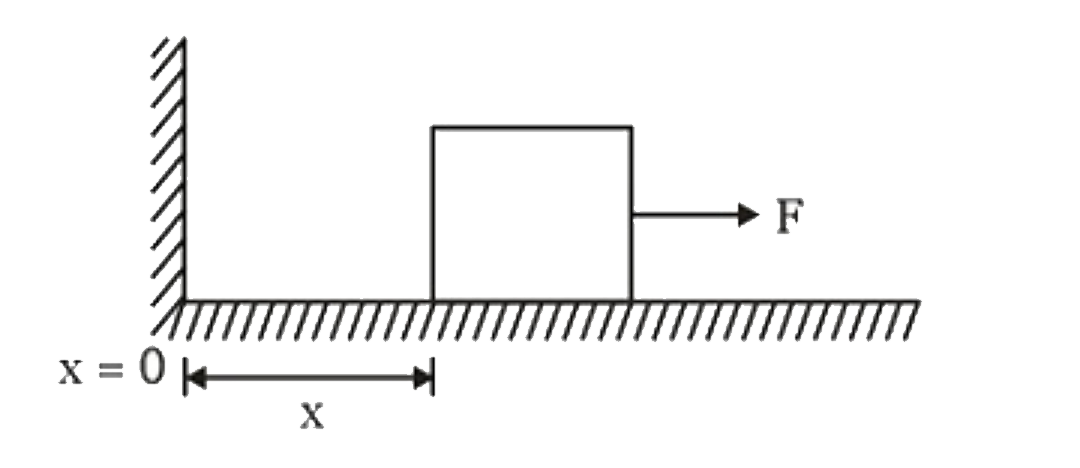 View Solution
View SolutionA small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
View SolutionA block of mass 2 kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between block and surface is 0.1. The work done by the applied force in 10 s is (Take g=10ms−2)
View Solution

