Mass center of a system of a segment of a uniform circular rod(arc)
Find location of mass center of a thin uniform rod bent into shape of an arc.
Consider a thin rod of uniform line mass density lambda(mass per unit length) and radius r subtending angle 2theta on its center 0.
The angle bisector OP is the line of symmetry, and mass center lies on it. Therefore if we assume the angle bisector as one of the coordinate axes say x-axis, y-coordinate of mass center becomes zero. Let two very small segments A and B located to the line of symmetry (x-axis). Mass center of these two segments is on P at a distance x=rcos∝ from center O.Total mass of these two elements is dm=2lambdardprop. Now using eq., we havexc=∫xdm−−−→M xc∫00(rcosα)(2λraα)λrθ=rsinθθ
Mass center of a thin uniform are shaped rod of radius r subtending angle 2theta at the center lies on its angle bisector at distance OC from the center. OC=rsinθθ
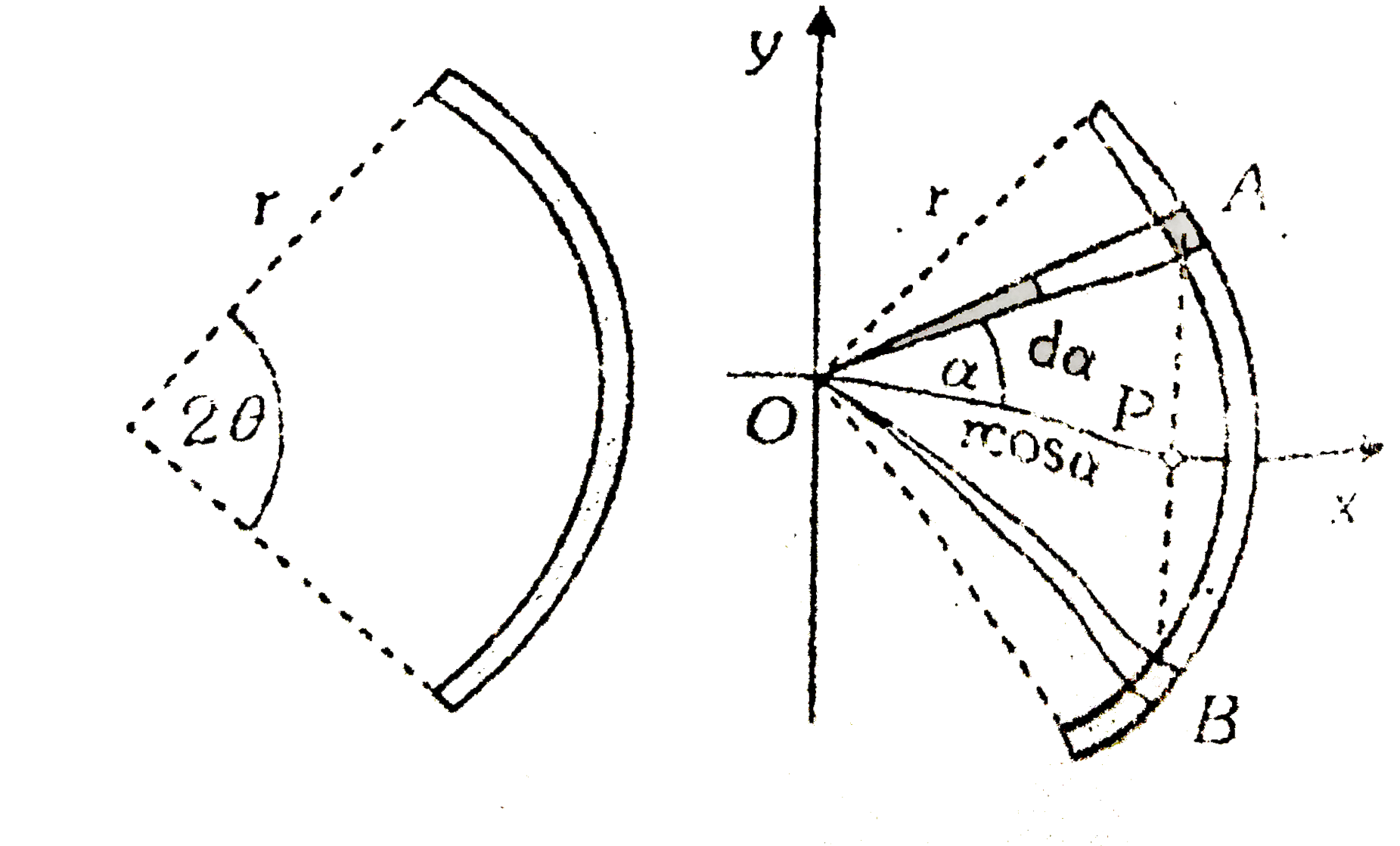
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Knowledge Check
A baseball bat of uniform density is cut at the location of its center of mass as shown in figure. The piece with the smaller mass is
 Athe piece on the rightBthe piece on the leftCBoth pieces have the same massDimpossible to determine.
Athe piece on the rightBthe piece on the leftCBoth pieces have the same massDimpossible to determine.The coordinates of the center of mass of the following quarter circular arc are
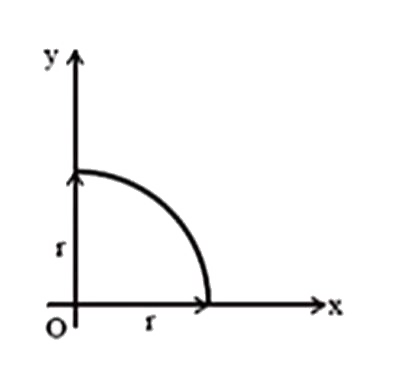 A(r2,r2)B(2r3,2r3)C(2rπ,2rπ)D(4rπ,4rπ)
A(r2,r2)B(2r3,2r3)C(2rπ,2rπ)D(4rπ,4rπ)A thick uniform wire is bent into the shape of the letter "U" as shown. Which point indicates the location of the center of mass of this wire ? A is the midpoint of the line joining mid points of two parallel sides of 'U' shaped wire.
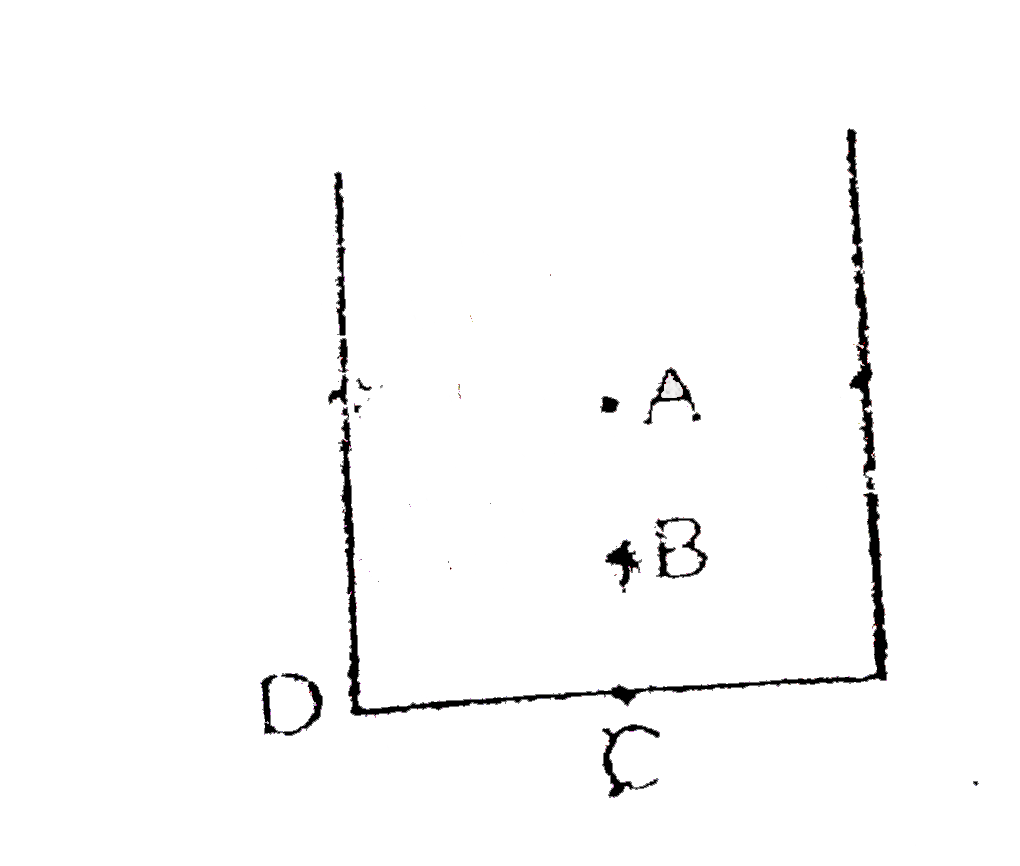 AABBCCDD
AABBCCDD
Find the center of mass of a uniform plate shown in Fig. 7.10a.
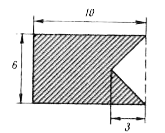
View SolutionThe coordinates of centre of mass of the following quarter circular arc is -

View SolutionLocate the center of mass.

View SolutionFind the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
View SolutionFigure shows a charge rod, bent in the from of an arc of a circle. The charge distribution on the rod is shown in figuire. The assembly is kept in a uniform electric field.

(a) Find the dipole moment of the rod.
(b) For small angular displacement the system find the time period of oscillation of the system.
View Solution
