As shown, a big box of mass M is resting on a horziontal smooth florr. On the bottom of the box there is a small block of mass m. The block is given an intial speed $v_{0}$ relative to the floor, and starts to bounce back and forth between the two walls of the box. Find the final speed of the box when the block has finally come to rest in the box :-

A

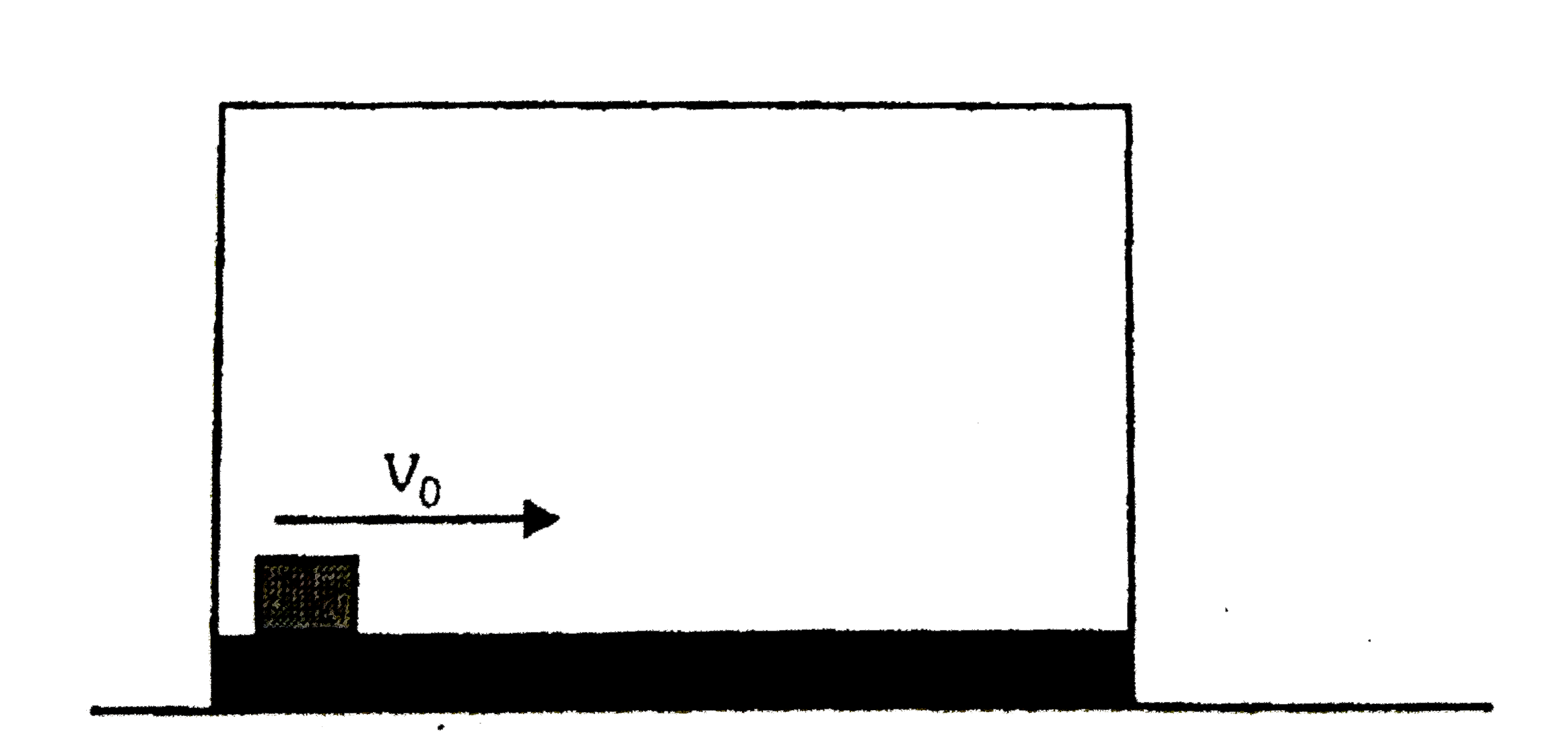
0

B

$v_{0}$

C

$\frac{m}{M} v_{0}$

D

$\frac{m}{m + M} v_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$F_{e x t} =$ zero,
$\to P =$ constant
$P_{i} = P_{f}$
Finally moving together with velocity v
$m v_{0} = (m + M) v$
$v = \frac{m v_{0}}{(m + M)}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block of mass $1 k g$ moving with a speed of $4 m s^{- 1}$ , collides with another block of mass $2 k g$ which is at rest. If the lighter block comes to rest after collision, then the speed of the heavier body is
A $2 m s^{- 1}$
B $1 m s^{- 1}$
C $1.5 m s^{- 1}$
D $0.5 m s^{- 1}$
Question 2 - Select One
The block of mass m is at rest. Find the tension in the string A .

Amg
B2 mg
C3 mg
D4 mg
Question 3 - Select One
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A $\sqrt{\frac{M}{M + n}} V$
B $\sqrt{\frac{m}{M + n}} V$
C $\frac{m}{M + n} V$
D $\frac{V}{2}$

ALLEN-CENTRE OF MASS-EXERCISE-I

Home
Ask Doubt
Profile