A particle of mass is connected by an inextensible string of length to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
0
The correct Answer is:C
Let distance moved by ring

Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-II
Explore 43 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-III
Explore 42 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V B
Explore 19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
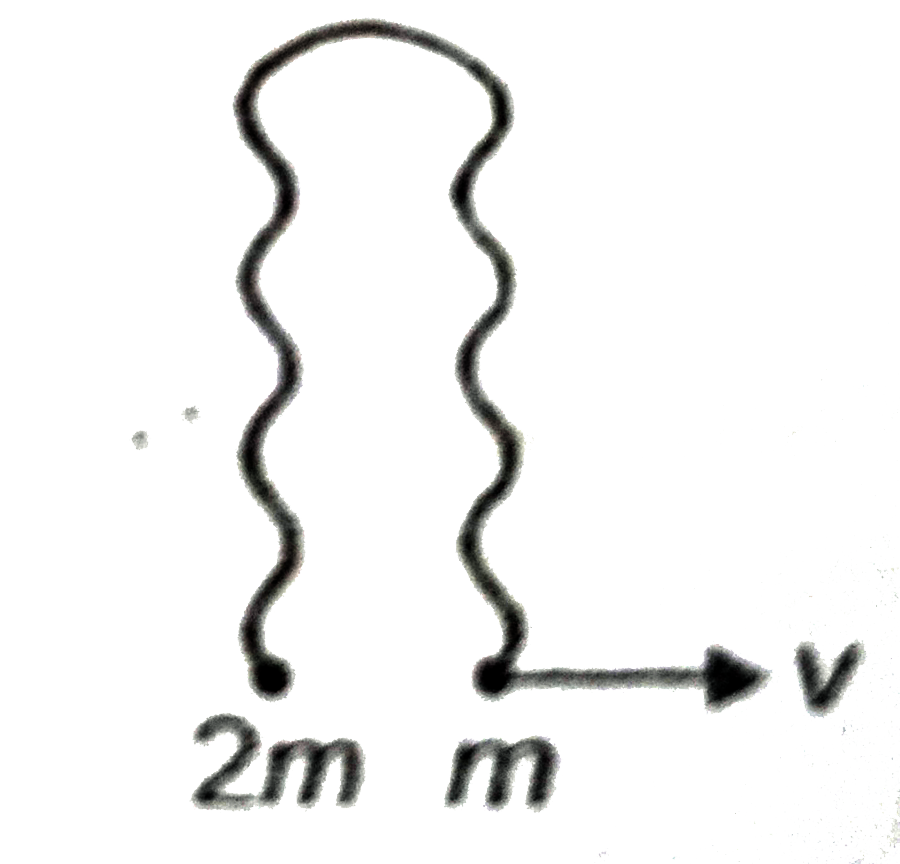
Two particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
View SolutionA pillar having square cross section of side length L is fixed on a smooth floor. A particle of mass m is connected to a corner A of the pillar using an inextensible string of length 3.5 L. With the string just taut along the line BA, the particle is given a velocity v perpendicular to the string. The particle slides on the smooth floor and the string wraps around the pillar.
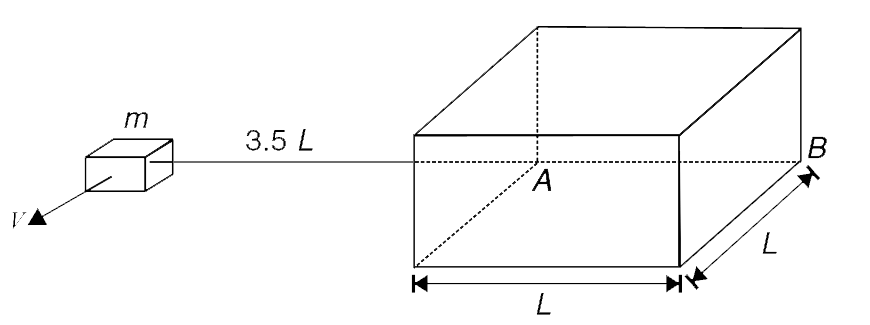
(a) Find the time in which the particle will hit the pillar. (b) Find the tension in the string just before the particle hits the pillar. Neglect any energy loss of the particle.
View Solution
Knowledge Check
A mass m connected to inextensible string of length l lie on a horizontal smooth ground. Other end of string is fixed. Mass m is imparted a velocity v such that string remains taut & motion occurs in horizontal providely stirng during the time string turns through 90∘
 A2mvBmvC√2mvDm√2v2−2gl
A2mvBmvC√2mvDm√2v2−2glA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√Tml
Two particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionA uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v0 parallel to the initial position of the rod.
(a) Calculate the acceleration of the centre of the rod immediately after the particle is projected.
(b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.

View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

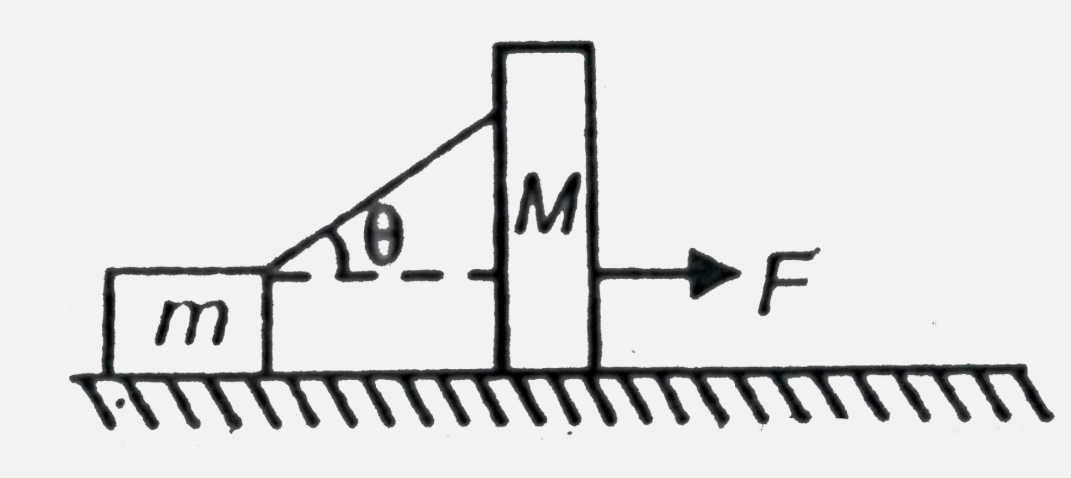
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
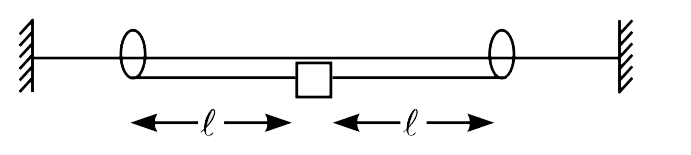
View SolutionA particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.
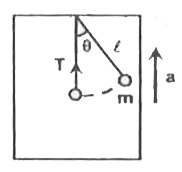
View Solution
