Two particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.

(i) COLM⇒(m+m)×0+Mv=(M+2m)v1v1=(MM+2m)v
(ii) COME⇒12MV2=[12m(v21+v22)]×2+12mv21
Net velocity v0=√v01+v22=v(√2M(M+m)(M+2m))
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
Two particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
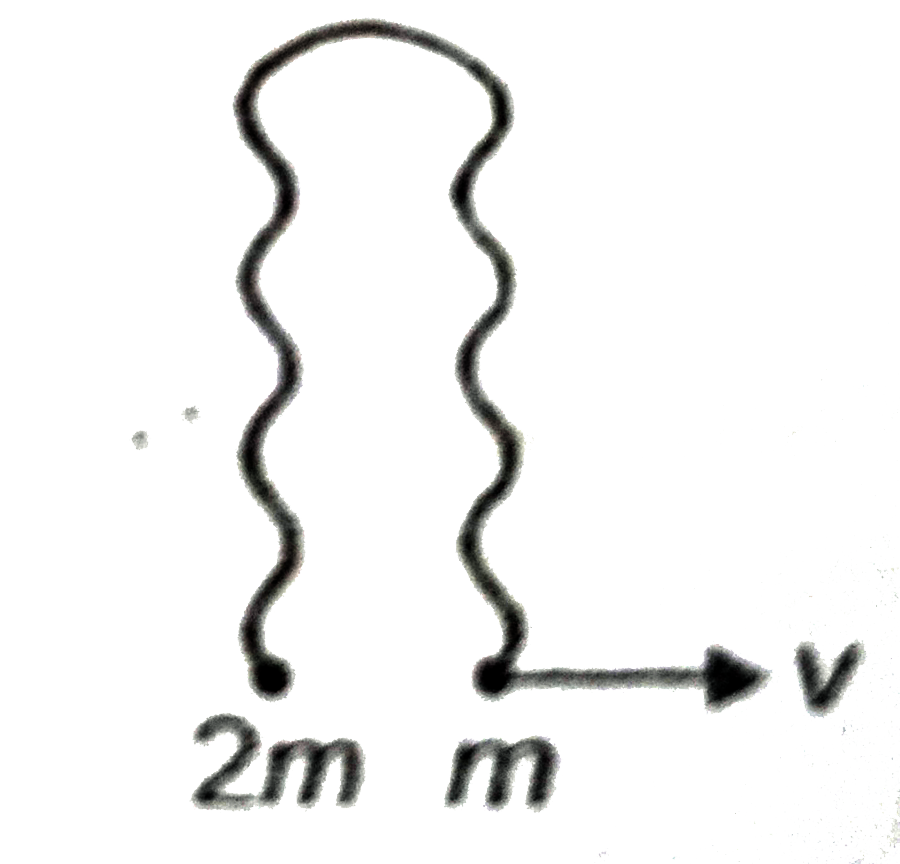 View Solution
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
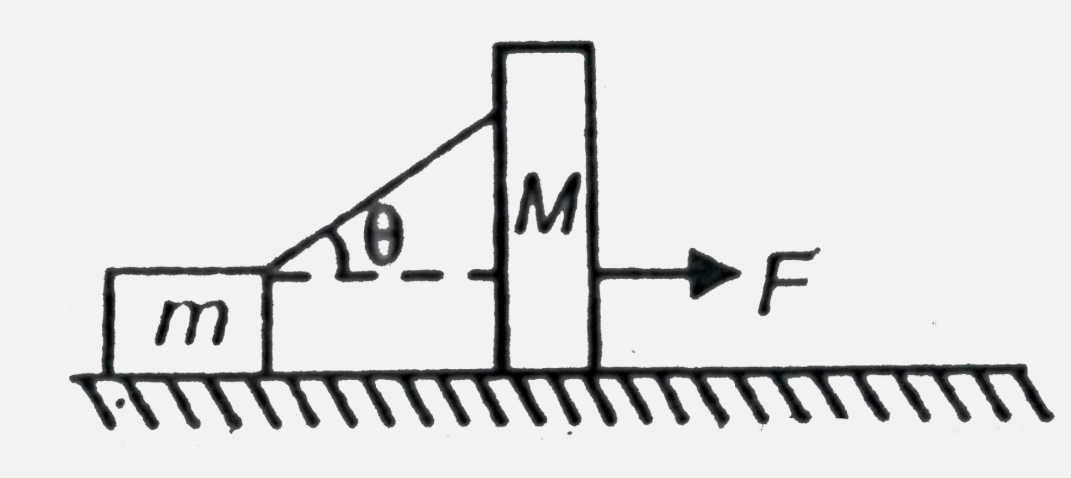 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A mass M is hung with a light inextensible string. Tension in horizontal part of string is.
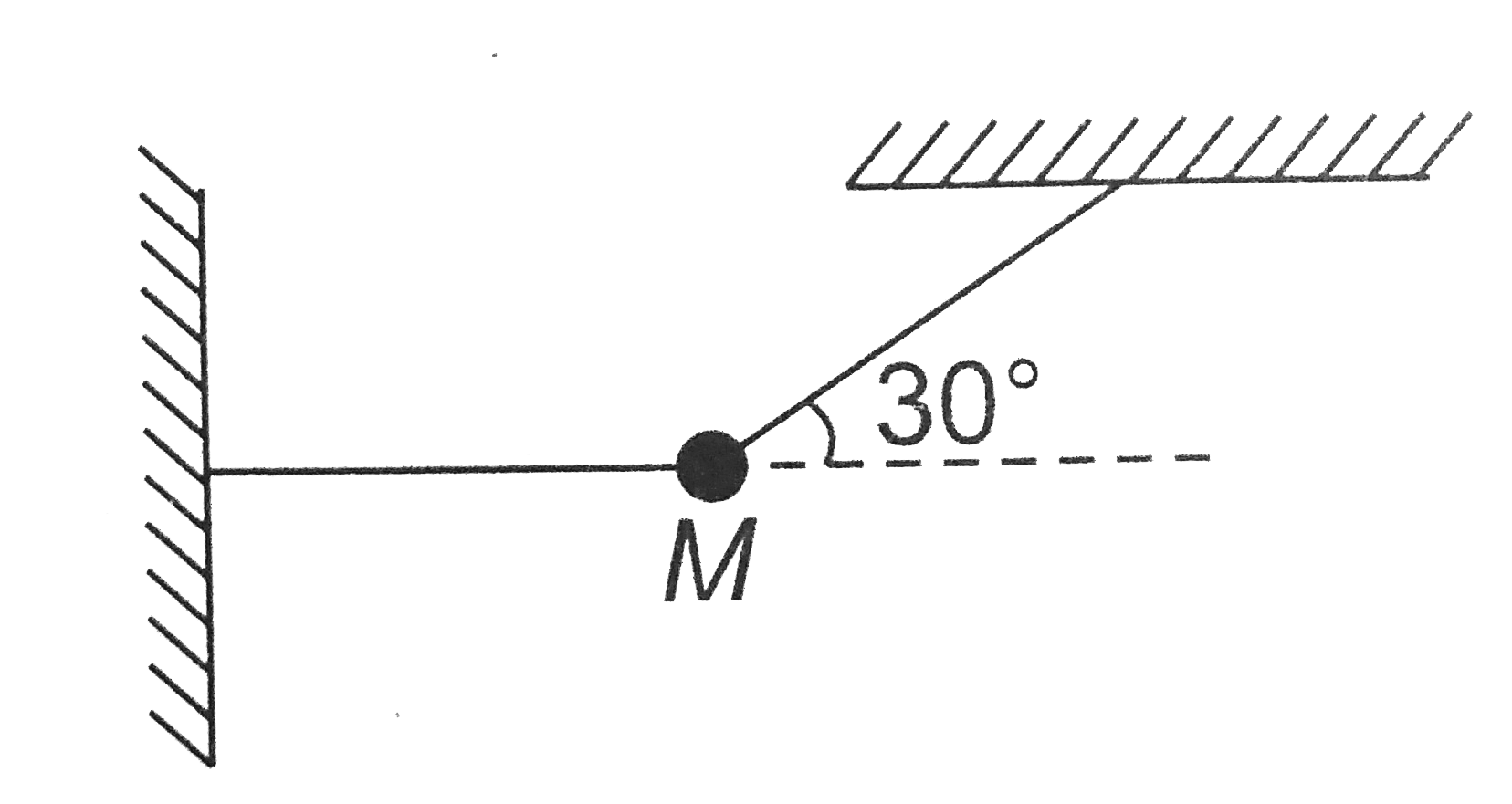 A√3MgB√2MgCmg√3Dmg2
A√3MgB√2MgCmg√3Dmg2 - Question 2 - Select One or More
A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
AThe string becomes slack when the partice reaches its highest pointBThe velocity of the particle becomes zero at the highest point.CThe kinetic energy of the ball in initial position was 12mv2=mgDThe particle again passes through the initial position. - Question 3 - Select One
A particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
A0B0.4C0.8D1.2
Three identical particles are placed on a horizontal smooth table, connected with strings as shown. The particle B is imparted a velocity V0=9m/s in horizontal direction perpendicular to the line ABC. Find speed of particle A when it is about to collide with C.
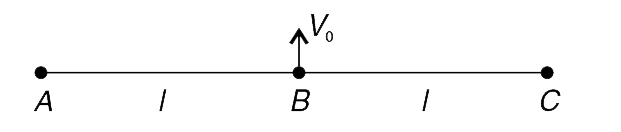 View Solution
View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
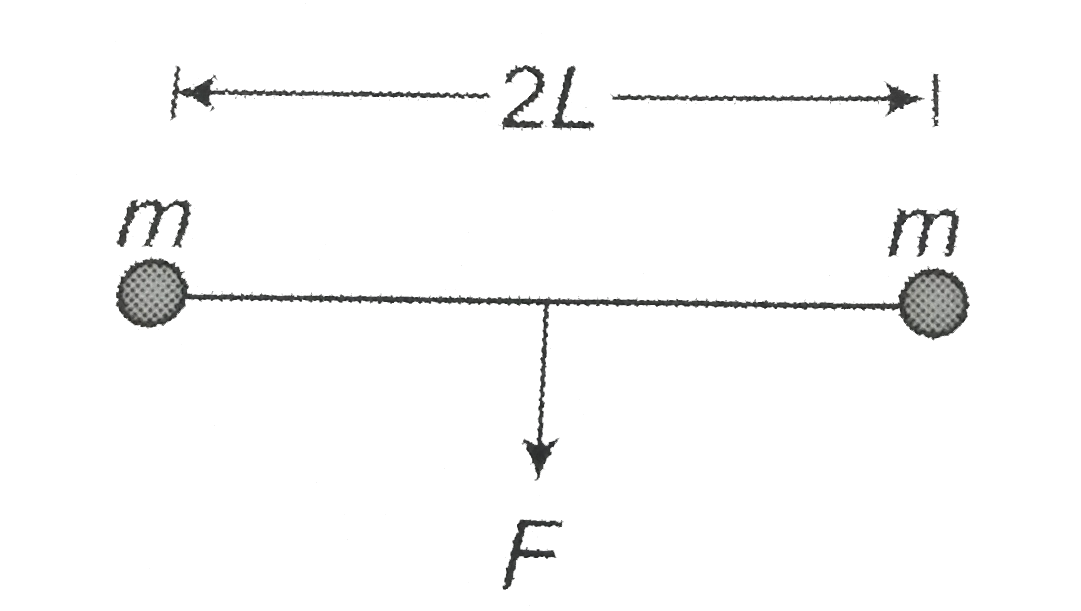 View Solution
View SolutionTwo particles, each of mass m, are connected by a light inextensible string of lenthe 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is :-
(i) along BA.
(ii) at an angle of 120∘ with AB
(iii) perpendicular to AB. In each case calculate (in teerms of m and u) the impulsive tension in the string.View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
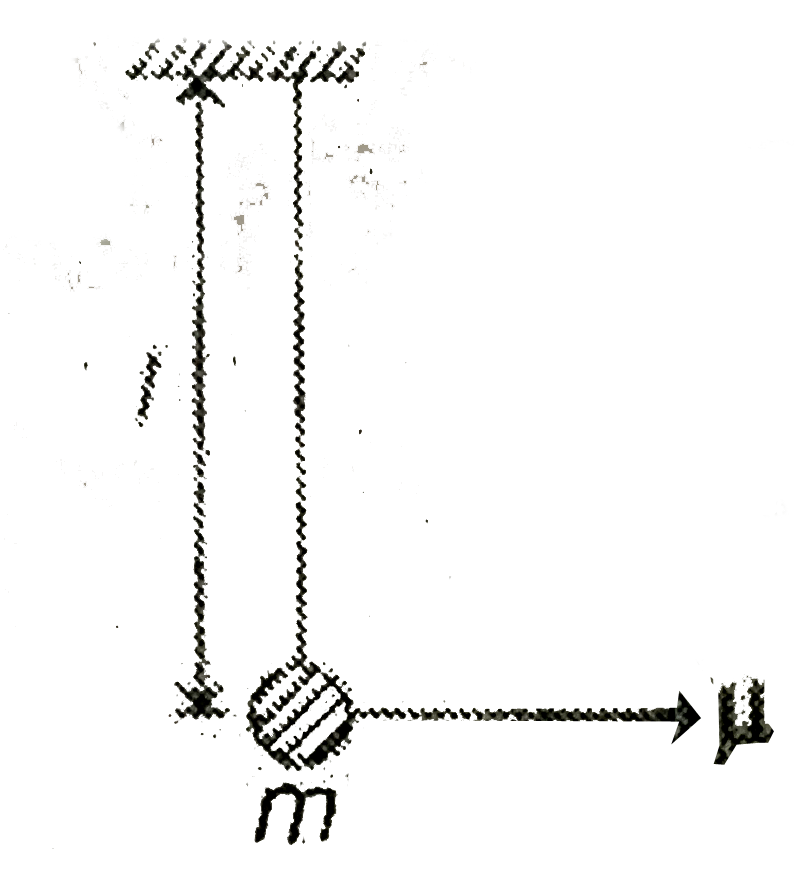
The tension in the string at an instant when acceleration of the particle is horizontal and √3g isView SolutionA particle of mass m1 is fastened to one end of a massless string and another particle of mass m2 is fastened to the middle point of the same string. The other end of the string being fastened to a fixed point on a smooth horizontal table. The particles are then projected, so that the two particles and the string are always in the same straight line and describe horizontal circles. Then, the ratio of rotations in the two parts of the string is :
View Solution

