A bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_
mv2L−d
mv2L+d
2mv2L−d
2mv2L+d
The correct Answer is:A
Δp= change in momentum =2mv
Δt= time between two collsion 2(L−d)v
∴ Force exerted on wall
=ΔpΔt=mv2(L−d)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A sphere of mass m slides with velocity v on as frictionless surface towards a smooth inclined wall as shown in figure. If the collision with the wall is perfectly elastic find a. the impulse imparted by the wall on the sphere b the impulse imparted by the floor on the sphere.
 View Solution
View SolutionA super-ball of mass m is to bounce elastically back and forth between two rigid walls at a distance d from each other. Neglecting gravity and assuming the velocity of super-ball to be v0 horizontally, the average force being exerted by the super-ball on each wall is
View Solution
Knowledge Check
- Question 1 - Select One
Two balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinity - Question 2 - Select One
Two balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinity - Question 3 - Select One
A parallel beam of particles of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
A2mnv2cosθB2mnv2cos2θC2mnvcosθD2mnvcos2θ
A heavy block A is made to move uniformly along a smooth floor with velocity V=0.01 m/s towards left. A ball of mass m=50g is projected towards the block with a velocity of u=100 m/s. The ball keeps bouncing back and forth between the block A and fixed wall B. Each of the collisions is elastic. After the ball has made 1000 collisions with the block and wall each, the distance between the block and the wall was found to be L=1.2m. Calculate the average force being experienced by the block due to collision at this instant. All collision are instantaneous
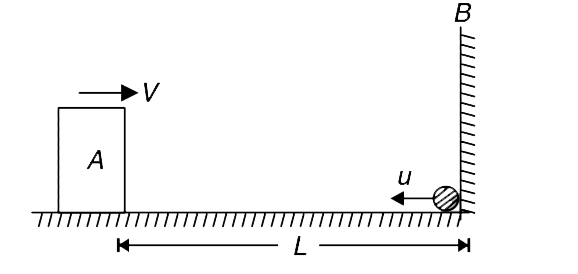 View Solution
View SolutionA nozzle throws a stream of gas against a wall with a velocity v much larger than the thermal agitation of the molecules. After collision of the molecules with wall the magnitude of their velocity remains same. Also assume that the force exerted on the wall by the molecule is perpendicular to wall. (This is not strictly true for a rough wall.) Find the pressure exerted on the wall. (n = number of molecules per unit volume, m = mass of a gas molecule)
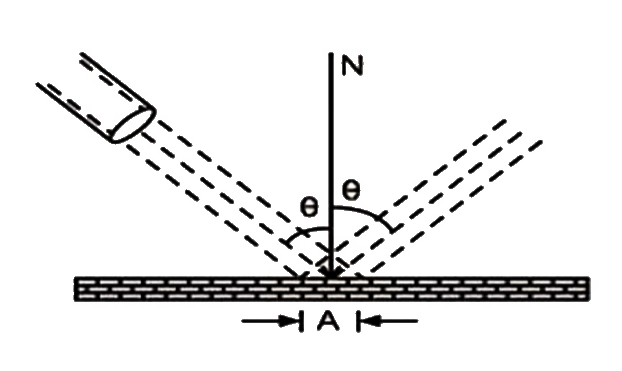 View Solution
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5 kg moving with a velocity of 2ms−1 strikes a wall normally and bounces back with the same speed. If the time of contact between the ball and the wall is one millisecond, the average force exerted by the wall on the ball is
View SolutionThe Fig. showns a string of equally placed beads of mass m, separated by distance. The beads are free to slide without friction on a thin wire. A constant force F act on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Supposed that all collisions are elastic,
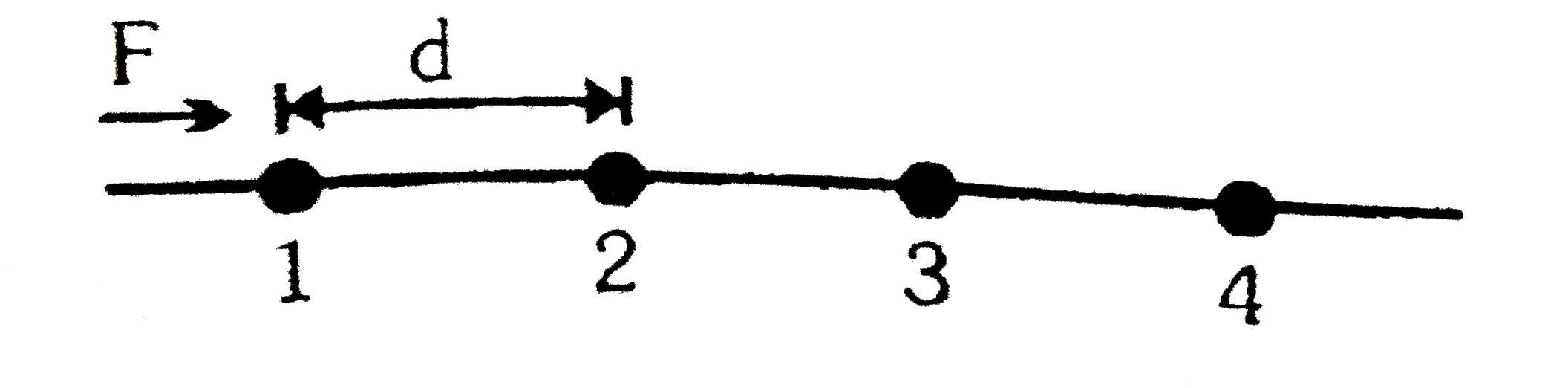 View Solution
View Solution

