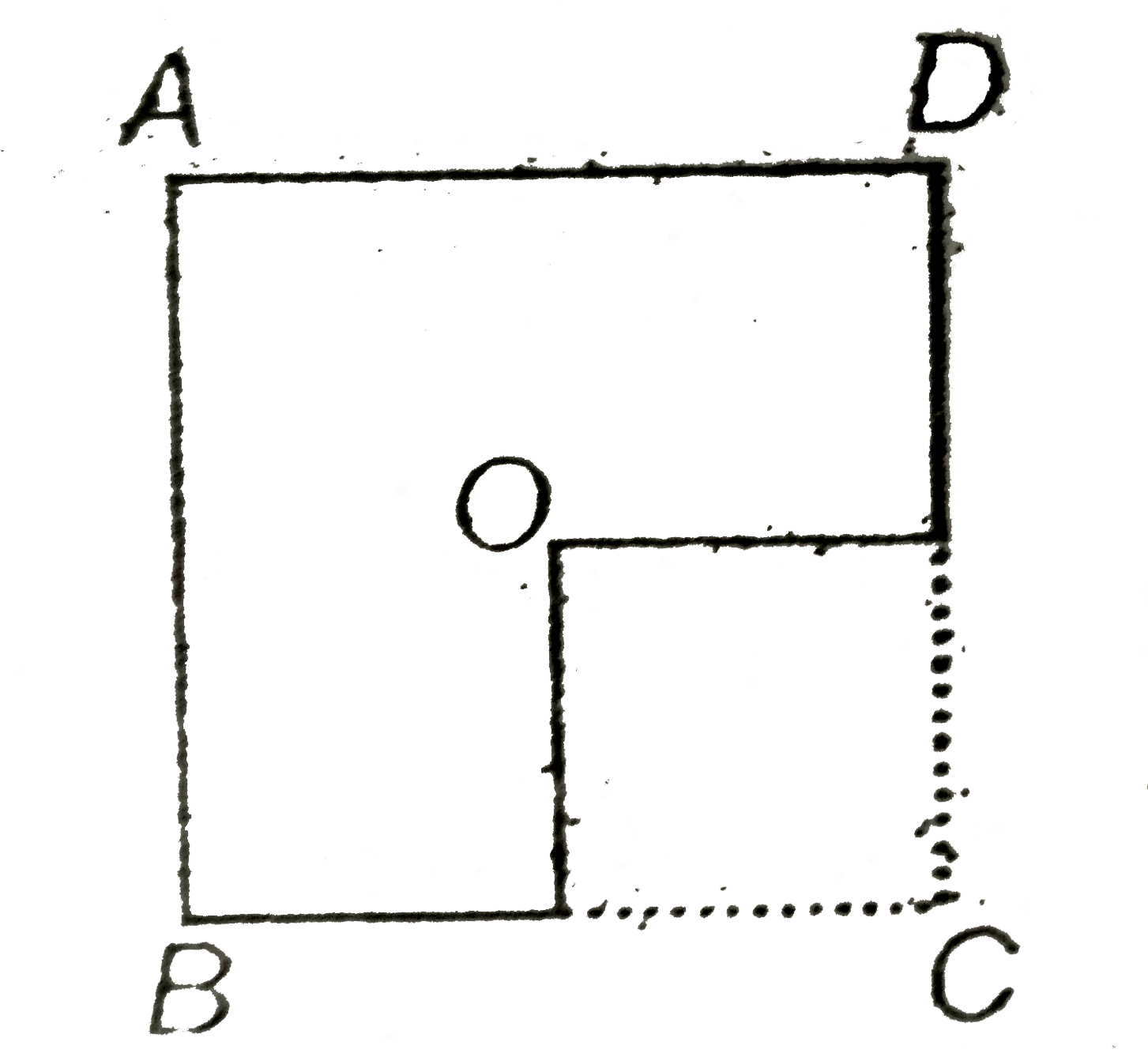
Fig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
Video Solution
Text Solution
The correct Answer is:(i) at O, (ii) diagonally from O to 3 (iii) along OY', (iv) at O (v) diagonally from O to 4 (vi) at O
(i) The centre of mass remains at O as the excluded masses are symmetrically placed. (ii) CM shifts from 0 to 3 diagonally (iii) CM shifts along OY (iv) CM does not shift. (v) CM shifts diagonally from 0 to 4 (vi) CM doesnot shift
|
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
42 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Knowledge Check
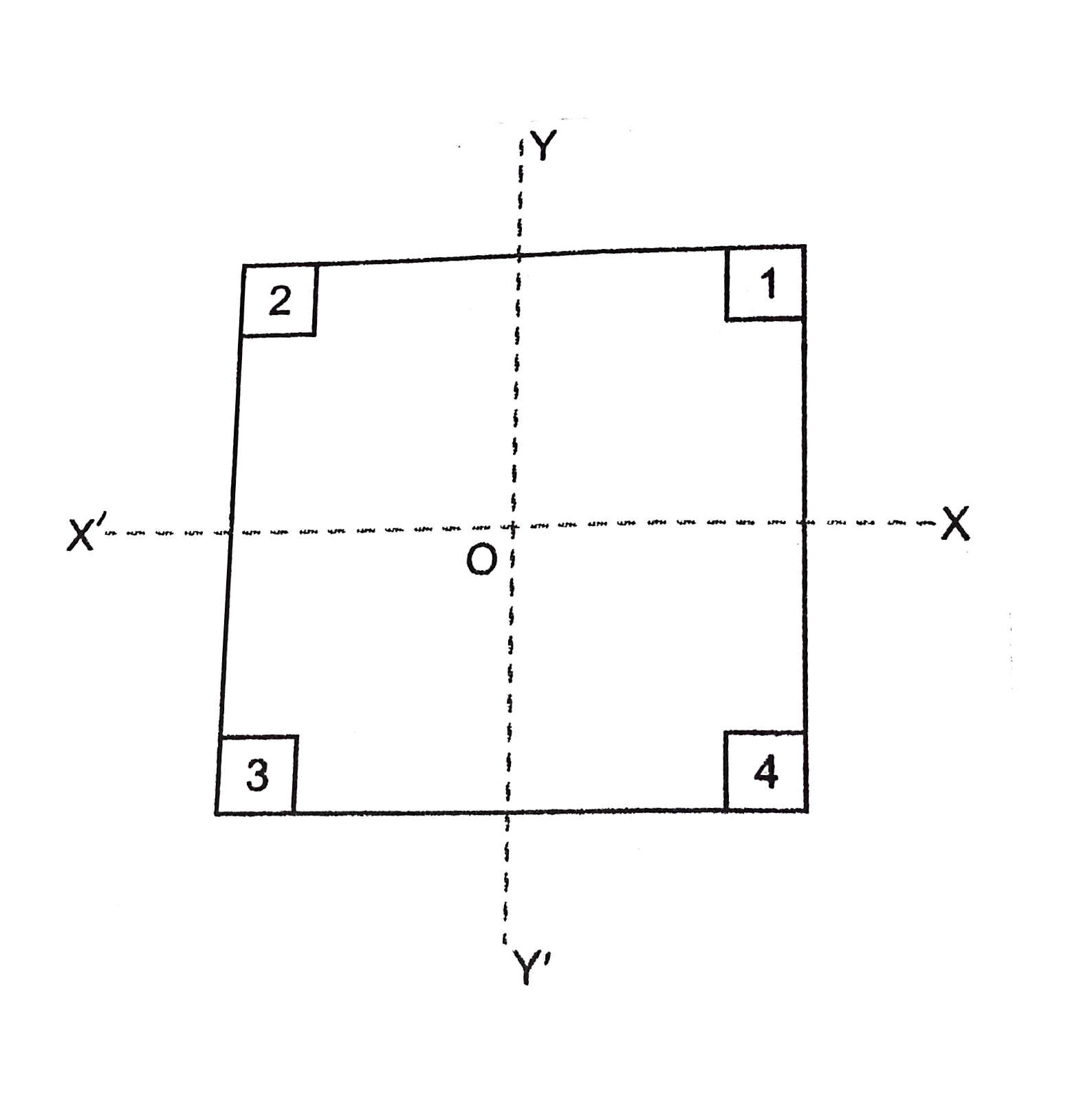
From a uniform square plate the shaped portions are removed as shown in figure. The coordinates of centre of mass of the remaining plate are x,y Axes and origon are shown in figure.
 Ax<a2,y<a2Bx>a2,y<a2Cx<a2,y>a2Dx>a2,y>a2
Ax<a2,y<a2Bx>a2,y<a2Cx<a2,y>a2Dx>a2,y>a2
From a uniform square plate of side a and mass m, a square portion DEFG of side a2 is removed. Then, the moment of inertia of remaining portion about the axis AB isA7ma216B3ma216C3ma24D9ma216A square matrix A is called orthogonal if
Where A' is the transpose of A.AA=A2BA'=A−1CA=A−1DA=A'
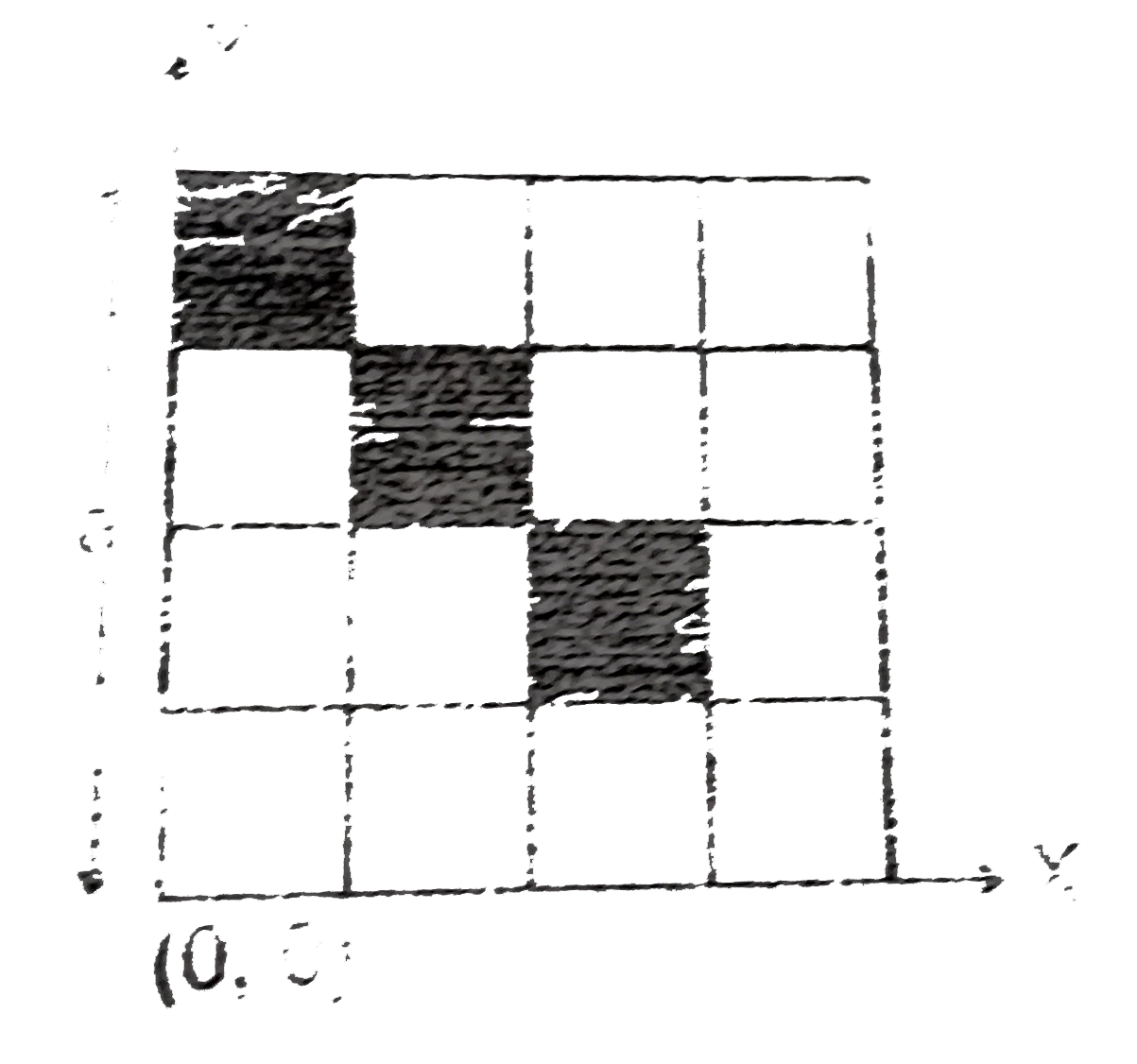
From a square sheet of uniform density , a portion a removed shown shaded in fig. Find the centre of msas of the remaining portion is the side of the square is α

View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionFind the area of the shaded region in Fig where ABCD is a square of side 14 cm.
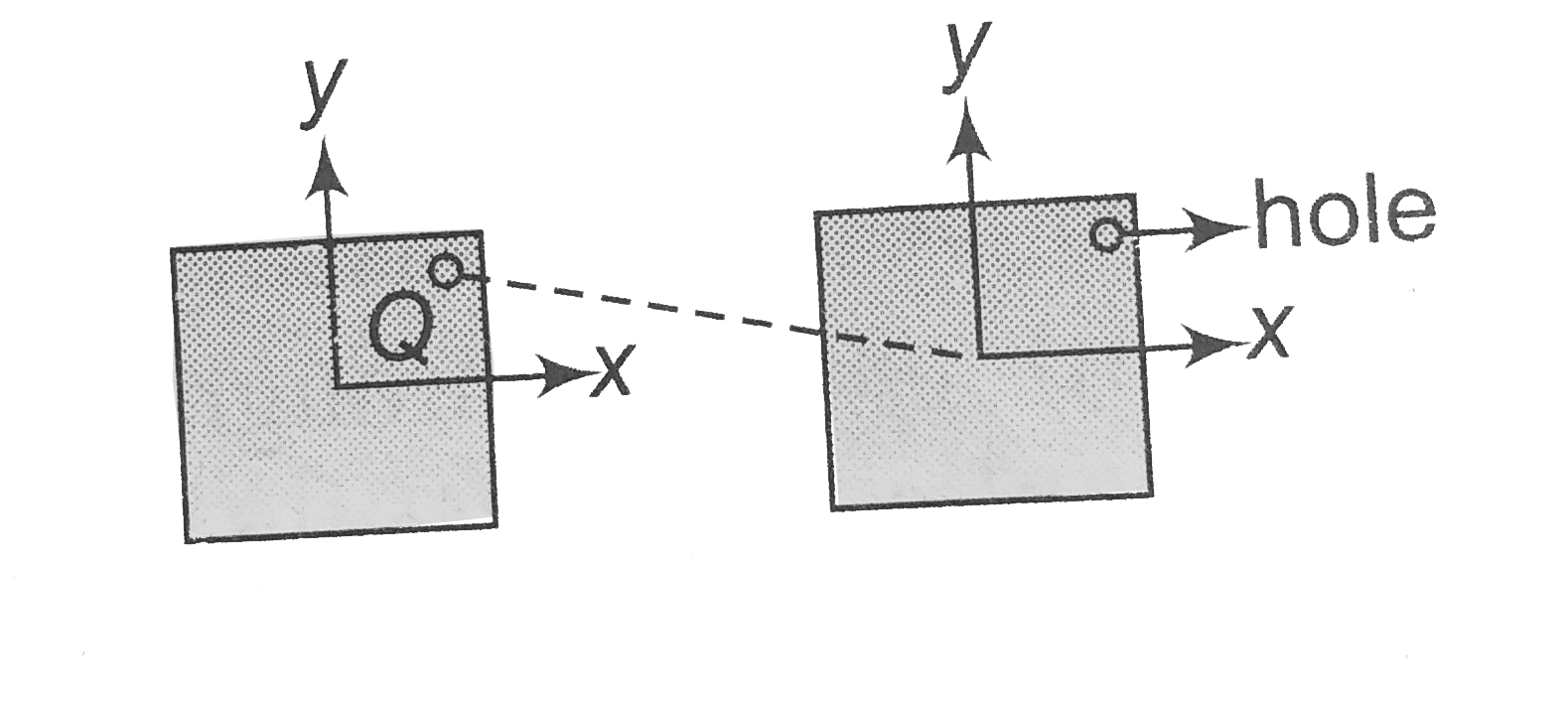
View SolutionA uniform square plate has a small piece Q of an irregular shape removed and guled to the centre of the plate leaving a hole behind in figure. The moment of inertia about the z-axis is then,
 .
.
View SolutionA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.

View Solution