In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
16
24
32
36
The correct Answer is:D
To find the area of triangle AEF in triangle ABC where D, E, and F are midpoints, we can follow these steps:
Step 1: Identify the given information
We know that:
- Triangle ABC has an area of 96.
- D is the midpoint of AB.
- E is the midpoint of DB.
- F is the midpoint of BC.
Step 2: Use the property of medians
Since D is the midpoint of AB, the median AF divides triangle ABC into two triangles of equal area. Therefore, the area of triangle ABF is half of the area of triangle ABC.
Area of △ABF=12×Area of △ABC=12×96=48
Step 3: Find the area of triangle ADF
Now, we can apply the median property again. Since DF is a median in triangle ABF, it divides triangle ABF into two triangles of equal area.
Area of △ADF=12×Area of △ABF=12×48=24
Step 4: Find the area of triangle BFD
Next, we need to find the area of triangle BFD. Since F is the midpoint of BC, we can apply the median property again. The area of triangle BFD is half of the area of triangle ABC.
Area of △BFD=12×Area of △ABC=12×96=48
Step 5: Find the area of triangle BEF
Now, since EF is the median in triangle BFD, it divides triangle BFD into two equal areas.
Area of △BEF=12×Area of △BFD=12×48=24
Step 6: Find the area of triangle FED
Now we can find the area of triangle FED. Since EF is the median in triangle BFD, we can again apply the median property.
Area of △FED=12×Area of △BFD=12×24=12
Step 7: Find the area of triangle AEF
Finally, we can find the area of triangle AEF by adding the areas of triangles ADF and FED.
Area of △AEF=Area of △ADF+Area of △FED=24+12=36
Conclusion
Thus, the area of triangle AEF is 36.
---
We know that:
- Triangle ABC has an area of 96.
- D is the midpoint of AB.
- E is the midpoint of DB.
- F is the midpoint of BC.
Since D is the midpoint of AB, the median AF divides triangle ABC into two triangles of equal area. Therefore, the area of triangle ABF is half of the area of triangle ABC.
Now, we can apply the median property again. Since DF is a median in triangle ABF, it divides triangle ABF into two triangles of equal area.
Next, we need to find the area of triangle BFD. Since F is the midpoint of BC, we can apply the median property again. The area of triangle BFD is half of the area of triangle ABC.
Now, since EF is the median in triangle BFD, it divides triangle BFD into two equal areas.
Now we can find the area of triangle FED. Since EF is the median in triangle BFD, we can again apply the median property.
Finally, we can find the area of triangle AEF by adding the areas of triangles ADF and FED.
Thus, the area of triangle AEF is 36.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 5
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 6
9 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 3
10 Videos
- LOGARITHMSBOOK - ALLENCHAPTER - LOGARITHMSEXERCISE - All Questions
92 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
12 Videos
Similar Questions
In the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View Solution
Knowledge Check
In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
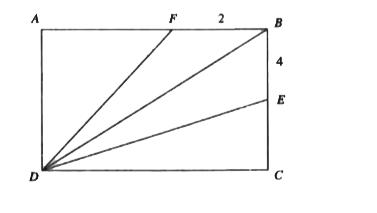 A18B23C30D42
A18B23C30D42In the figure, ABCD is a rectangle and points E, F, G and H are midpoints of its sides. What is the ratio of the area of the shaded region to the area of the un-shaded region in the rectangle?
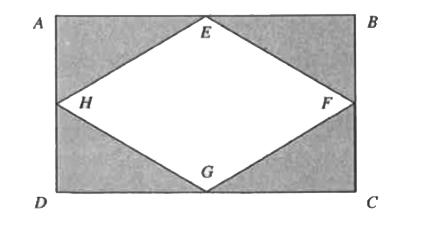 A1:1B1:2C2:1D1:3
A1:1B1:2C2:1D1:3

In the figure above, each arc is a semicircle. If S is the midpoint of PQ and Q is the midpoint of PR, what is the area of semicircles PS to the area of semicircles PR?
View SolutionIn ΔABC, E is mid-point of side AB and EBCD is a parallelogram. If the area of ΔABC is 80 cm, find the area of parallelogram EBCD.
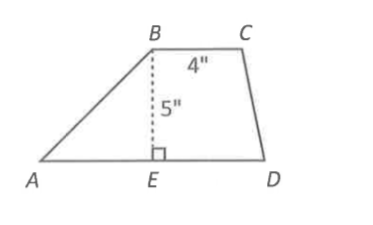
View SolutionABCD is a quadrillateral, with AD parallel to BC (see figure). E is a point between A and D such that BE represents the height of ABCD and E is the midpoint of AD. If the area of triangle ABE is 12.5 square inches, what is the area of ABCD?
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionIn triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
View Solution
